我们已经认识了线段、角、三角形、长方形等基本图形，当这些图形重重叠叠地交错在一起时就构成了复杂的几何图形。要想准确地计数这类图形中所包含的某一种基本图形的个数，就需要仔细地观察，灵活地运用有关的知识和思考方法，掌握数图形的规律，才能获得正确的结果。
要准确、迅速地计数图形必须注意以下几点：
（1）弄清被数图形的特征和变化规律；
（2）按一定的顺序数，不重复，不遗漏。
数出下图中有多少条线段。
要正确解答这类问题，我们需要按照一定的顺序来数，做到不重复，不遗漏。从图中可以看出，从A 点出发的不同线段有3 条：AB、AC、AD；从B 点出发的不同线段有2 条：BC、BD；从C 点出发的不同线段有1 条：CD。因此，图中共有线段：3+2+1=6（条）。对于此类问题，还可以用公式：1+2+…+（总点数-1）求解。
数出下图中有多少条线段。
❶
❷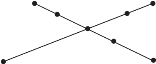
数一数下图中有多少个锐角。
数角的方法和数线段的方法类似，图中的5 条射线相当于线段上的5 个点，因此，要求图中有多少个锐角，可根据公式：1+2+3+…+（总射线数-1）求得：1+2+3+4=10（个）。
数一数下面图中各有多少个锐角？
❶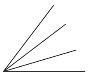
❷
(https://www.xing528.com)
❸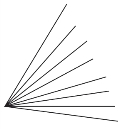
数一数下图中共有多少个三角形。
图中AD 边上的每一条线段与顶点O 构成一个三角形，也就是说，AD 边上有几条线段，就构成了几个三角形，因为AD 上有4 个点，共有线段：1+2+3=6（条），所以图中有6 个三角形。
数一数下面图中各有多少个三角形。
❶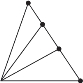
❷
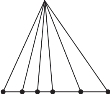❸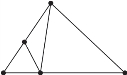
数一数下图中共有多少个三角形。
与前一个例子相比，图中多了一条线段EF，因此三角形的个数应是AD 和EF上面的线段与点O 所围成的三角形个数的和。以EF 上的线段为底边的三角形有：1+2+3=6（个），以AD 上的线段为底边的三角形也是：1+2+3=6（个），所以图中共有三角形：6×2=12（个）。
数一数下面图中各有多少个三角形。
❶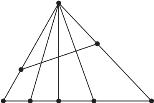
❷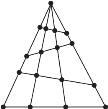
数一数下图中有多少个长方形。
数长方形与数线段、数三角形的方法类似。可以这样思考，图中的长方形的个数取决于AB 或CD 边上的线段，AB 边上的线段条数是：1+2+3=6（条）。所以，图中有6 个长方形。
数一数下面图中各有多少个长方形。
❶
❷
❸
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
