供应链社会责任的相互影响与协同治理的研究成果

5.4.1.1　问题描述

本书试图分别构建在制造商直接负责回收（M-回收）和委托零售商回收（R-回收）两种回收渠道下，由单个上游制造商和单个下游零售商构成的两级闭环供应链决策模型。在正向供应链中，制造商以单位商品价格为ω批发给零售商，零售商以单位价格p销售给消费者；在逆向供应链中，制造商、零售商可分别从消费者手中回收废旧产品，然后零售商将再制造产品以单位价格为m销售给制造商进行回收处理。在回收的过程中，回收方会收取单位服务费为A，当A＞0时表示回收方向消费者支付的单位费用；当A＞0时表示回收方向消费者收取的单位费用。为保证回收的经济性，设m-A＞0。根据上述描述，构建本书的闭环供应链的决策模型如图5.3所示：

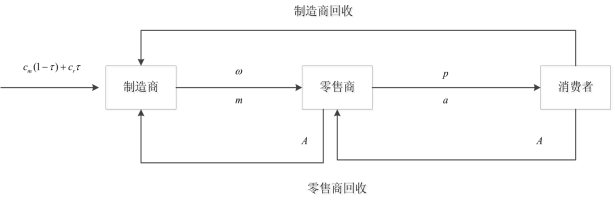
图5.3　闭环供应链回收渠道决策模型

5.4.1.2　模型假设

本书基于上述文献梳理，为简化供应链的复杂结构，提出如下符合经济学理论的基本假设。

假设1：与Savaskan[141]、罗甸[142]等研究假设相同，本书假设新产品的质量与回收再制造的产品质量相同，且消费者对于两种产品具有相同的接受程度。

假设2：将新产品的单位生产成本设为cm，回收再制造产品的单位成本设为cr，回收价格设为m。假设制造商再次进行新产品的生产时，需要先将废旧产品进行回收以此作为原材料；同时，为了保证制造商有一定的动力进行废旧产品的回收，需要满足制造商从零售商手中回收的废旧产品费用低于废旧产品单位节约成本，即m＜Δ（设Δ=cm（1-τ）+cr，且Δ＞0）且废旧品的回收率满足0＜τ＜1。

假设3：与Savaskan的研究假设相同，在不考虑回收废旧产品的变动成本的前提下，回收成本与废旧产品的回收率存在以下函数关系，即回收成本函数为：

其中k为回收规模的成本系数，且k＞b（Δ-m）2。

假设4：假设制造商或零售商的CSR投入水平为λ，参考已经广泛应用在经济、管理文献中的努力成本函数[148]，将制造商或零售商的CSR投入成本分别记为

(www.xing528.com)

其中，参数ξ为CSR投入范围参数，表示CSR投入的效率。

假设5：假设制造商向零售商的批发价格、零售商的产品售价分别记为ω、p，且ω＜p。

在不考虑闭环供应链的制造商、零售商的CSR投入影响时，市场需求函数记为：

其中a表示市场容量，且a＞0；b表示消费者对新产品价格的敏感程度，且b＞0。

假设6：制造商或零售商在进行CSR投入时会对市场需求带来一定的影响，参考文献[149]，将CSR投入带来的利润设为

其中λ表示CSR的投入水平，且0≤λ≤1。λ=0表示企业不进行CSR投入；λ=1表示企业尽最大努力进行CSR投入。

假设7：假设在闭环供应链的决策中，所有的决策成员都是完全理性的，以企业自身利润最大化作为决策的标准。

模型中的符号表示及说明如表5.2所示：

表5.2　符号表示及说明

注：在制造商负责回收时，相关变量均采用上标M表示，在零售商负责回收时，相关变量均采用上标R表示；关于制造商的相关变量均采用下标m表示，关于零售商的相关变量均采用下标r表示；在制造商进行CSR投入的情况中，相关变量均用下标1表示，在零售商进行CSR投入的情况下，相关变量均用下标2表示；集中决策中的相关变量用下标S表示。