供应链闭环决策与社会责任影响研究

通过以上假设，构建非对称信息条件下不考虑CSR投入的闭环供应链决策模型，零售商以及制造商的利润函数分别如下：

应用逆向归纳法：

（1）对Πr关于P求偏导，令可得：

（2）再对制造商的期望利润E（Πm）关于其批发价格ω求偏导，令可得：

并将ω*带入p中得

所以

为了保证结果有意义，需要满足Q大于0，因此2a＞ea+b[cm-（Δ-m）η]总成立。由此可知：

由此可以推出各变量与利润之间的变化关系以及相应的结论，如下定理5.1、5.2、5.3并进行证明如下。

定理5.1：（1）产品的批发价格、产品的零售价格均与市场潜力均值成正相关关系，而产品的销量以及零售商利润与之成反比。（2）产品的批发价格、销售价格同制造商产品回收率成反比，相反，产品的销量以及零售商的利润则同制造商产品回收率成正比。

证明：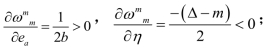

综上，定理5.1得证。

定理5.2：制造商的利润与市场潜力均值之间是成正相关的关系；且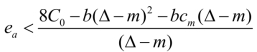成立时，存在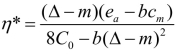使得制造商的利润取得最优值。

证明：(www.xing528.com)

（1）因为有

成立，所以制造商的利润与市场潜力均值成正相关。

（2）又由

可得：

成立时满足0＜η＜1条件。所以在此前提下，当时，总成立，此时制造商的利润随着回收率的增加而增加；当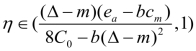时，成立，此时制造商的利润与自身的产品回收率之间呈现反比关系。所以当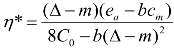时，制造商利润取得最优值。

综上，定理5.2得证。

定理5.3：ea＜3bcm+5b（Δ-m）-2a 成立时，有使得供应链整体利润取得最优值。

证明：由可得：

当ea＜3bcm+5b（Δ-m）-2a 时，存在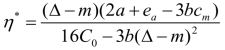成立。

当时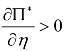成立，所以供应链整体利润与回收率之间成正比；

当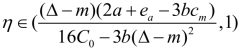时，成立，所以供应链整体利润随着与回收率之间成反比；因此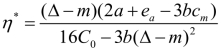时，供应链整体利润取得最优值。

综上，定理5.3得证。