航空材料力学性能检测：F分布的应用

1.F分布概率密度函数

数理统计学中，除了对单子样正态分布的母体平均值μ和母体标准差σ是否为某一定值进行统计检验外，还需对两个子样的母体均值是否相同（即μ₁=μ₂）、母体标准差是否相同（即σ₁=σ₂）进行检验。前面已介绍了应用t分布对μ₁=μ₂的检验，现在介绍对σ₁=σ₂的检验原理。需要说明的是，只有通过了对σ₁=σ₂的检验，才可应用t分布进行μ₁=μ₂的统计检验。

一般利用F分布来检验“两个服从正态分布的子样是否来自标准差相同的两个母体”，即检验两个母体标准差σ₁和σ₂是否相等。这里简要介绍F分布的分布规律和检验原理。F分布的概率密度函数p（F）为

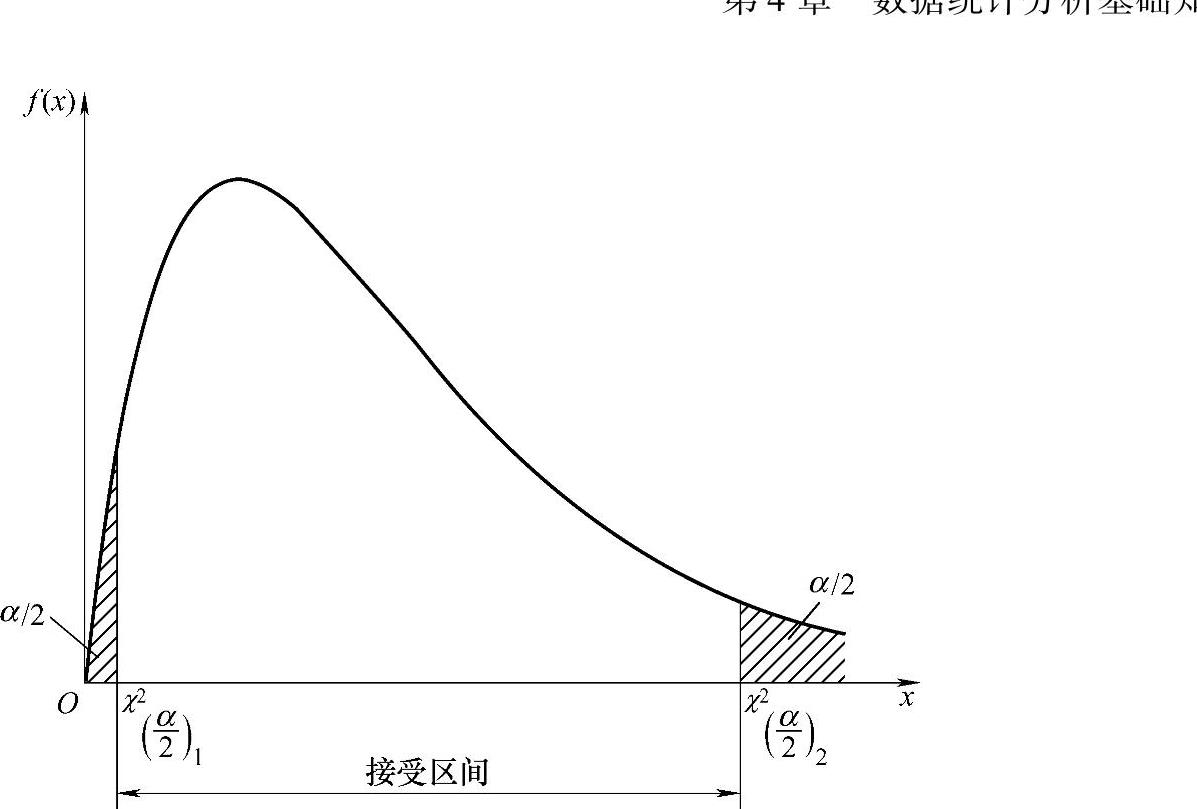
图4-10 χ²分布在给定显著度α下的接受区间

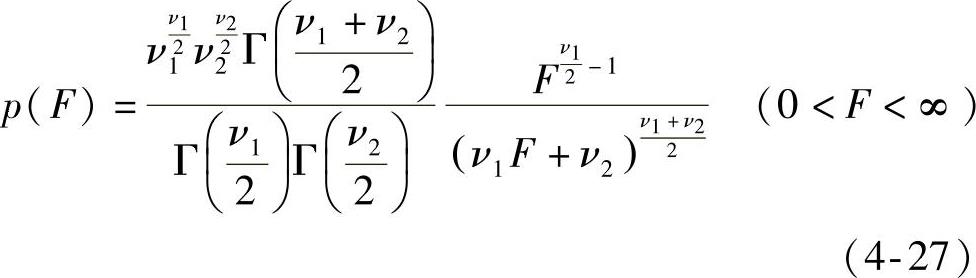
式中 F——F分布的随机变量；

ν₁、ν₂——F分布的两个母体参数，分别称为“分子自由度”和“分母自由度”；

Г（α）——Г函数，可由Г函数表查值得到。

F分布的概率密度曲线如图4-11所示。

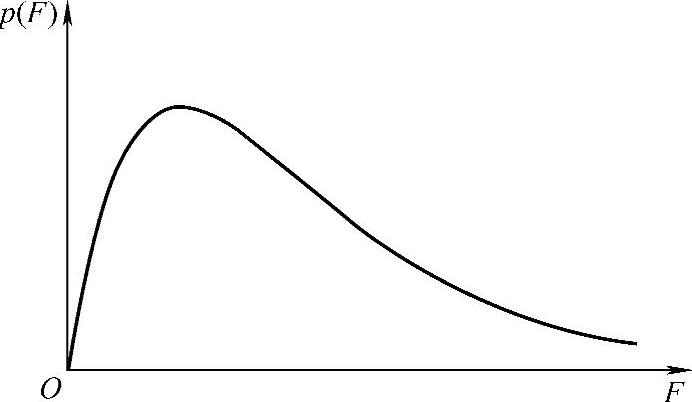
图4-11 F分布的概率密度曲线(www.xing528.com)

2.F分布检验两个正态分布子样的母体标准差是否相同

对于两个子样，第一个子样服从正态分布N（μ₁；σ₁）且大小为n₁，第二个子样服从正态分布N（μ₂；σ₂）且大小为n₂。可以证明式（4-28）中的F变量服从F分布，且对应的自由度分别为ν₁=n₁-1、ν₂=n₂-1。

式中 s₁、s₂——两个正态分布的子样标准差；

σ₁、σ₂——两个正态分布的母体标准差。

现做统计假定：“两个子样所服从的两个正态分布母体标准差相同，即σ₁=σ₂”，则式（4-28）可简化为

可利用式（4-29）的F变量对σ₁=σ₂进行双侧统计检验。检验时，首先将两个正态分布的子样标准差s₁和s₂代入式（4-29）中，计算得到F值。然后在给定显著度α和自由度ν₁=n₁-1、ν₂=n₂-1的条件下，查阅F分布数值表，从而得到图4-12所示的接受区间（a，b）。如果计算的F值在此区间内，则接受两个正态分布的母体标准差σ₁=σ₂的假定；否则，则不接受σ₁=σ₂的假定。

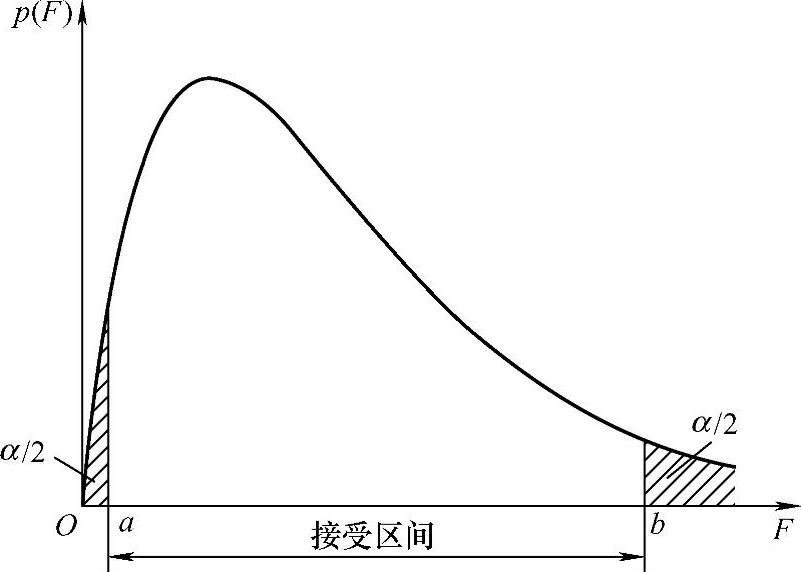
图4-12 F分布在给定显著度α下的接受区间

当统计假定σ₁=σ₂成立时，s₁和s₂之间的差异纯属偶然误差所致。因此，s₁和s₂应相差无几，F值也必将在1左右偏摆。当σ₁和σ₂存在显著差异时，F值将远大于1或远小于1，从而落在接受区间以外。为了制表的方便，一般F分布数值表只给出接受区间的上限F_α/2（即图4-12中的b点）。因此，在计算F值时，约定子样方差数值较大的作为分子，较小的作为分母。这样，进行显著性检验时，用计算得到的恒大于1的F值与数值表给出的上限值F_α/2互相比较即可。若F＞F_α/2，则拒绝假设；若F＜F_α/2，则接受假设。