航空材料力学性能检测：t分布及应用

1.t分布概率密度函数

t分布是数理统计学中一个重要的统计分布。t分布的用途很广，这里只介绍应用t分布对正态分布的母体平均值进行统计检验的原理和主要结论。t分布的概率密度函数h（t）为

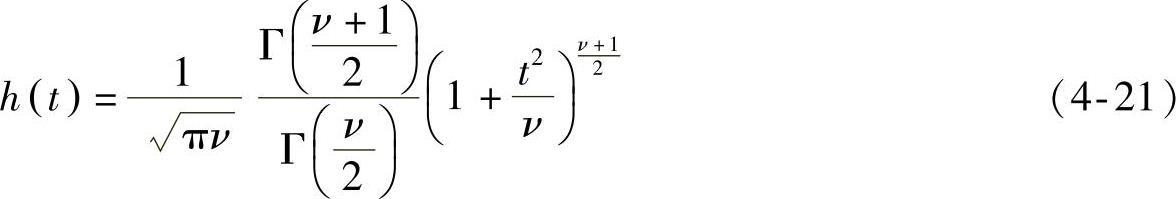
式中 t——t分布的随机变量；

ν——t分布的母体参数，称为“自由度”；

Г（α）——Г函数，可由Г函数表查值得到。

t分布的概率密度曲线如图4-7所示。由图4-7可见，t分布的概率密度曲线与前述的标准正态分布概率密度曲线类似，都以纵坐标轴为对称轴。进一步的数学证明指出：当ν→∞时，t分布趋于标准正态分布。实际上，当ν≥30时，两者已经十分接近。

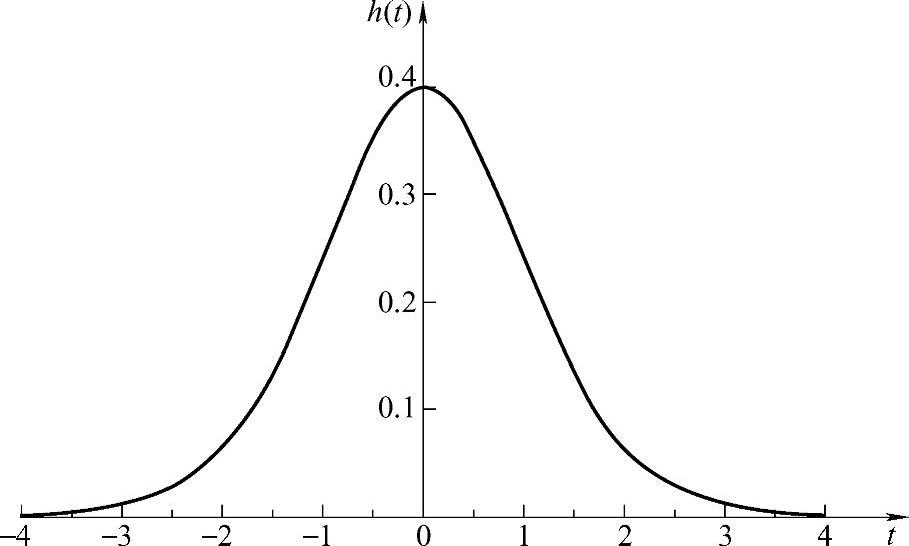
图4-7 t分布的概率密度曲线

2.t分布检验一个正态分布子样的母体均值是否等于某值

对于一个大小为n且服从正态分布N（μ；σ）的子样，可以证明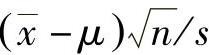：服从t分布，且对应的自由度ν=n-1。可令t变量为

式中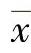 ——正态分布的子样平均值；

s——正态分布的子样标准差；(www.xing528.com)

n——子样大小；

μ——正态分布的母体平均值。

可以利用t变量与正态分布母体平均值μ的关系[即式（4-22）]对μ进行统计检验。假定正态分布母体平均值为某一定值μ₀，但此假定是否能够让人信服（即有足够的置信度），则需进行双侧统计检验。检验时，将假定的正态分布母体平均值μ₀和子样特征值x、s代入式（4-22）中，计算得到t₀值。然后在给定显著度α和自由度ν=n-1的条件下，查阅t分布数值表，得到接受区间的上下限±t_α/2（见图4-8），即接受区间为（-t_α/2，+t_α/2）。如果计算的t₀值在此区间内，则接受正态分布母体平均值μ=μ₀的假定；否则，则不接受μ=μ₀的假定。

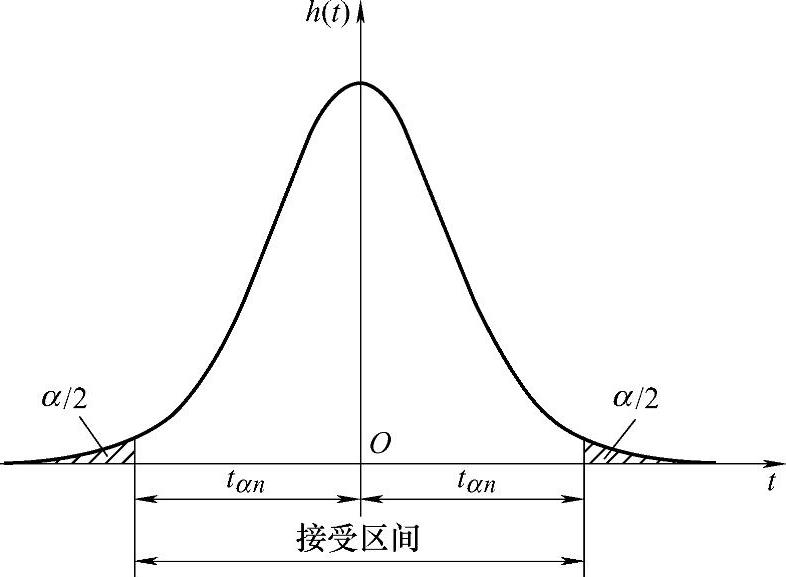
图4-8 t分布在给定显著度α下的接受区间

3.t分布检验两个正态分布子样的母体均值是否相同

对于两个子样，第一个子样服从正态分布N（μ₁，σ₁）且大小为n₁，第二个子样服从正态分布N（μ₂；σ₂）且大小为n₂。在两个母体的标准差相等（即具备σ₁=σ₂的方差齐性）的条件下，可以证明式（4-23）中的t变量服从t分布，且对应的自由度ν=n₁+n₂-2。

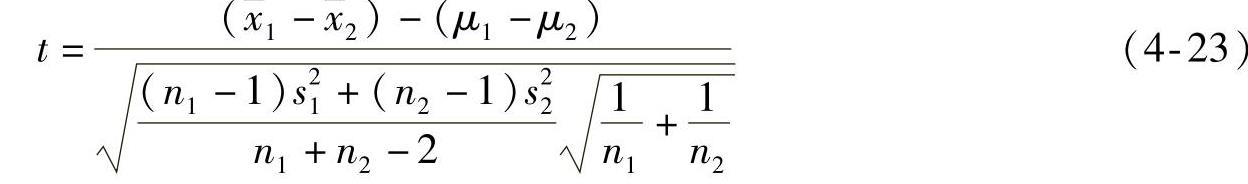
式中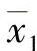 、s₁、n₁——第一个子样的子样平均值、子样标准差和子样大小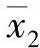；、s₂、n₂——第二个子样的子样平均值、子样标准差和子样大小；

μ₁、μ₂——两个正态分布的母体平均值。

现做统计假定：“两个子样所服从的两个正态分布母体平均值相同，即μ₁=μ₂”，则式（4-23）可简化为

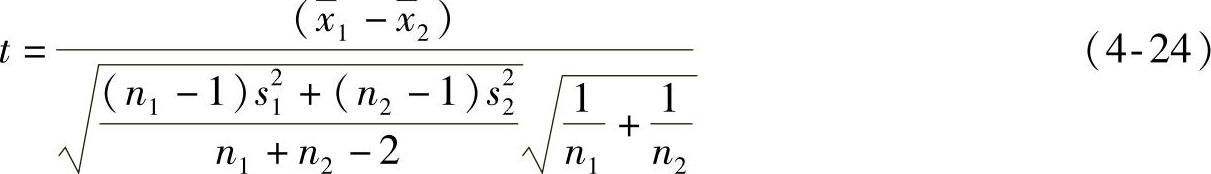
可利用式（4-24）的t变量对μ₁=μ₂进行双侧统计检验。检验时，首先将两个正态分布的各特征值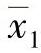、、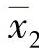s_l、S₂、n₁、n₂代入式（4-24）中，计算得到t值。然后在给定显著度α和自由度ν=n₁+n₂-2的条件下，查阅t分布数值表，从而得到图4-8所示的接受区间（-t_α/2，+t_α/2）。如果计算的t值在此区间内，则可接受两个正态分布的母体平均值μ₁=μ₂的假定；否则，则不接受μ₁=μ₂的假定。