1.威布尔分布概率密度函数
在可靠性领域,威布尔分布得到了广泛应用。威布尔分布的优点在于存在有最小安全寿命,即100%可靠度的安全寿命。按照正态分布理论,只有当对数安全寿命xp=lgNp趋于-∞时(即Np=0时),可靠度才等于100%。显然,这是不符合实际情况的(事实上,构件存在一个最小安全寿命使其对应的可靠度趋近于100%),这也是采用正态分布处理此类问题的理论不足之处。此时,如采用威布尔分布理论,则在极高可靠度范围(99.99%~100%)内给出的安全寿命(或最小安全寿命)是比较符合实际情况的。
另外,正态分布适用于中、短寿命区的情况,而威布尔分布则不仅限于此。对于疲劳寿命大于106次循环的长寿命区,众多试验结果也近似符合威布尔分布,从而能得到长寿命区的安全寿命。但由于威布尔概率密度函数的数学形式较繁,这使得它在统计应用中受到一些限制。
研究表明,在恒定幅值的循环载荷作用下,各试件疲劳寿命N为一随机变量,且N服从威布尔分布,则N的威布尔概率密度函数可写为
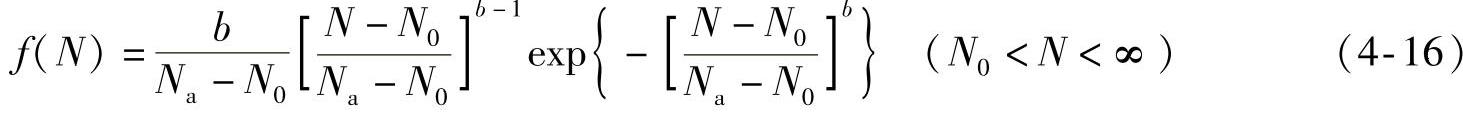
式中 N0——最小寿命参数;
Na——特征寿命参数;
b——威布尔形状参数(斜率参数)。
由此可见,威布尔概率密度函数中含有三个待定参数(在正态分布中只有两个,即μ和σ),因此能更完善地拟合试验数据点。
 (https://www.xing528.com)
(https://www.xing528.com)
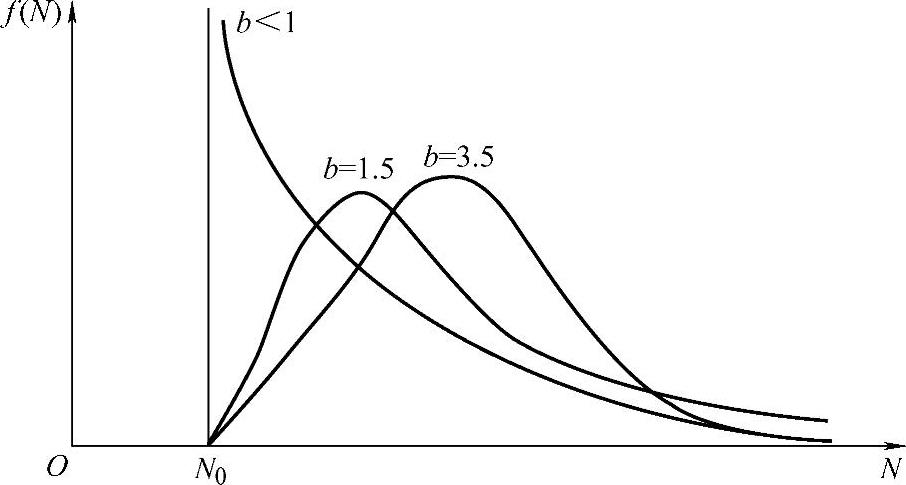
图4-6 威布尔分布的概率密度曲线
威布尔分布的概率密度曲线如图4-6所示。由图4-6可见,当b=1时,f(N)为一简单的指数概率密度函数。当b=2时,f(N)称为瑞利概率密度函数。当b=3~4时,接近正态概率密度函数。曲线高峰通常偏斜向左,偏斜程度随b而变化。对于b>1的情况,当N=N0时曲线与横坐标轴相交,存在有大于零的最小寿命值N0。差值(Na-N0)越大,曲线外形越扁平,分散性越大。曲线右端延伸至无限远处,以横坐标轴为渐近线。
2.威布尔分布的参数估计
威布尔分布的三个母体参数(N0,Na,b)的估计量的符号分别记为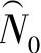 、
、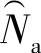 、
、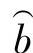 。由一致性要求和无偏性要求推导(推导过程略)得到
。由一致性要求和无偏性要求推导(推导过程略)得到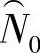 、
、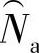 、
、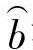 满足以下四式:
满足以下四式:
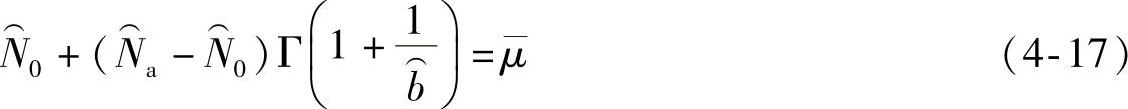
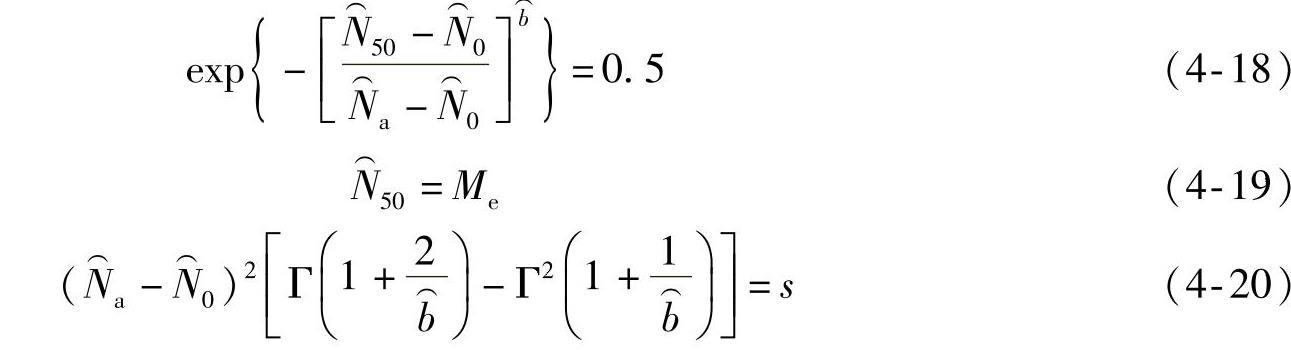
式中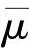 、s、Me——子样平均值、子样标准差和子样中值;
、s、Me——子样平均值、子样标准差和子样中值;
Г(α)——Г函数,可由Г函数表查值得到。
由此可见,只要将子样特征值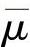 、s、Me代入以上四式,再联合求解,即可得到威布尔母体参数的三个估计量(
、s、Me代入以上四式,再联合求解,即可得到威布尔母体参数的三个估计量(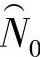 、
、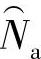 、
、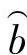 )。
)。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




