正态分布及其应用——从理论到实践

1.一般正态分布

在数理统计学中，最重要的一个频率分布为正态分布，也称高斯分布。多年来，人们对各种研究对象（如对数疲劳寿命、零件尺寸、材料性能、化学成分和测量误差等）进行了大量的统计分析。根据这些研究对象的分布结果发现了正态分布，并得到了其概率密度函数f（x），其函数表达式为

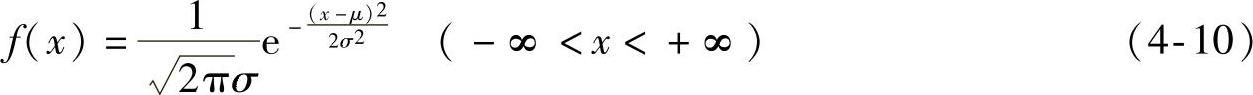
式中 e——自然对数的底，且e=2.718；

μ、σ——正态分布的两个分布参数，μ为母体平均值，σ为母体标准差。

显然，当μ和σ已知时，其概率密度函数f（x）就会确定。

正态分布的概率密度曲线如图4-4所示。由图4-4可见，当x=μ时，f（x）为极大值。曲线的对称轴位于横坐标μ处。在x=μ±σ处，曲线存在拐点。对称轴左右两部分曲线向外延伸，并且以横坐标轴为曲线的渐近线。曲线的形状由母体标准差σ决定。σ越大，曲线外形越扁平，表示分散性越大；σ越小，曲线外形越狭高，表示分散性越小。若已知μ和σ，正态分布的概率密度曲线就可完全确定。一般采用符号N（μ；σ）表示母体平均值为μ、母体标准差为σ的正态分布。

2.标准正态分布

对于正态分布，令其概率密度函数中的母体平均值μ=0、母体标准差σ=1，即可得到所谓的标准正态分布。标准正态分布通常用符号N（0；1）表示，其概率密度函数见式（4-11），相应的概率密度曲线如图4-5所示。

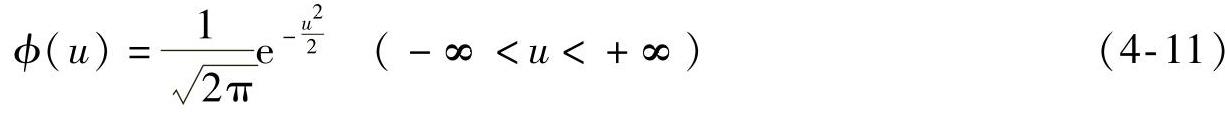
对于一般的正态分布N（μ；σ），可通过式（4-12）将其转换为标准正态分布N（0；1）。这样转换的好处是可以利用已知的标准正态分布表来查得随机变量U小于u_p时的概率Φ（u_p）。

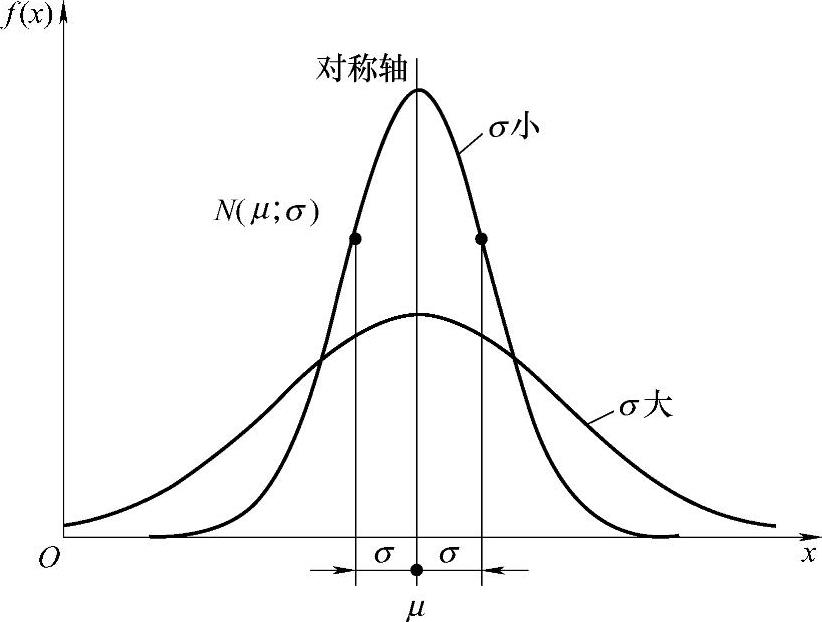
图4-4 正态分布的概率密度曲线

(www.xing528.com)

图4-5 标准正态分布的概率密度曲线

式中 U——标准正态分布的随机变量；

X——一般正态分布的随机变量；

μ、σ——一般正态分布的分布参数。

3.对数正态分布

大量的统计结果显示，试件的疲劳寿命N是一个随机变量，且N不服从正态分布，但是对数疲劳寿命lgN一般是服从正态分布的。因而，可通过式（4-13）将疲劳寿命N转换为正态分布的随机变量X。这样转换的好处是可以方便地利用正态分布的概率密度函数和相应特征值对试件的疲劳寿命进行统计分析和处理。

X=lgN （4-13）

4.正态分布的参数估计

一般来说，各种分布的母体参数都属于理论值，无法精确无误地确定其大小。例如，某事件服从正态分布N（μ；σ），那么其母体平均值为μ和母体标准差为σ一般都是未知的。为了近似得到这些母体参数，一般采用现有的子样数据来估计它们。用子样数据来估计母体的参数（如μ和σ）属于点估计量的问题。虽然这种点估计方法只是对母体参数的近似，但是为了保证这种估计的有效性，一般须满足一致性要求和无偏性要求。

正态分布母体平均值μ的估计量的符号记为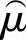，母体标准差σ的估计量的符号记为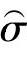。由一致性要求和无偏性要求推导（推导过程略）得到和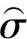计算式分别为

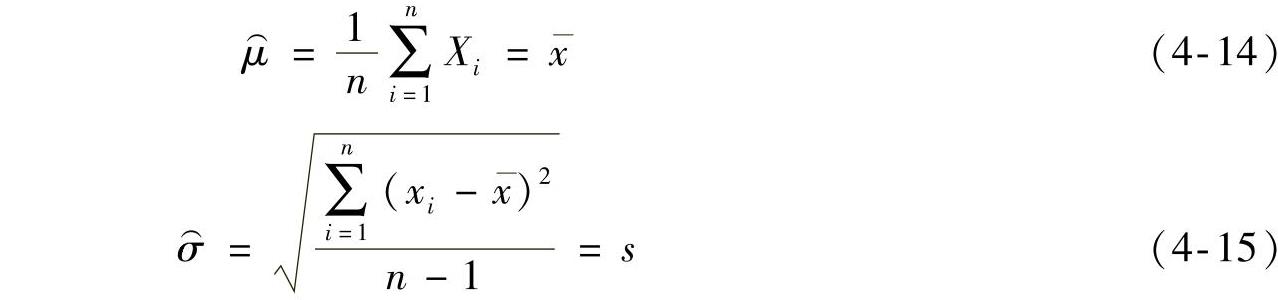
可见，子样的特征值恰好与正态分布母体参数（真值）的估计值和完全相等，即子样平均值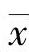等于、子样标准差s等于。