航空材料力学性能检测：平均值与中值

疲劳统计的基本任务是要根据子样的统计性质来推断母体的性质。而这种推断须借助于数学分析的方法，所以，须求出几个观测数据的特征值，以此来代表子样的统计性质。常用的子样特征值可分为两类：一类是表示数据集中位置的，如平均值和中值；另一类是表示数据分散性质的，如标准差（标准偏差）、方差和变异系数等。

如果从母体中随机地抽取一个大小为n的子样，取得了n个观测数据（x₁，x₂，…，x_n），则这n个数据的平均值称为“子样平均值”，以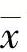表示，即

如果从母体中随机地抽取一个大小为n的子样，取得了n个观测数据（x₁，x₂，…，x_n），则这n个数据的平均值称为“子样平均值”，以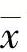表示，即

显然子样平均值反映了数据的平均性质。各个观测数据可看作是围绕它而分布的，因此子样平均值能够表示数据的集中位置。

“中值”也是一种表示数据集中位置的特征值，中值也被称为中位数。将一组数据按大小顺序排列，居于正中间位置的数值，称为这组数据的子样中值，用符号M_e表示。例如，在一次疲劳试验中，测得一组5个试件的疲劳寿命（按大小顺序排列）为

（376，535，565，604，901）×10³次

此时，由于观测数据的总数为奇数，因此子样中值就是居于正中（第3个）的那个数，即M_e=565×10³次。当观测数据的总数为偶数时，如以上试验再增加一个试件，测得6个试件的疲劳寿命（同样按大小顺序排列）为

（376，535，565，604，629，901）×10³次(www.xing528.com)

则子样中值为居于中间位置的两个（第3个和第4个）数据的平均值，即M_e=（565+604）/2×10³=585×10³次。

显然子样平均值反映了数据的平均性质。各个观测数据可看作是围绕它而分布的，因此子样平均值能够表示数据的集中位置。

“中值”也是一种表示数据集中位置的特征值，中值也被称为中位数。将一组数据按大小顺序排列，居于正中间位置的数值，称为这组数据的子样中值，用符号M_e表示。例如，在一次疲劳试验中，测得一组5个试件的疲劳寿命（按大小顺序排列）为

（376，535，565，604，901）×10³次

此时，由于观测数据的总数为奇数，因此子样中值就是居于正中（第3个）的那个数，即M_e=565×10³次。当观测数据的总数为偶数时，如以上试验再增加一个试件，测得6个试件的疲劳寿命（同样按大小顺序排列）为

（376，535，565，604，629，901）×10³次

则子样中值为居于中间位置的两个（第3个和第4个）数据的平均值，即M_e=（565+604）/2×10³=585×10³次。