航空材料弹性模量的物理意义

由胡克定律式（2-14）和式（2-16）可知，当应变为1个单位（e=1或γ=1）时，弹性模量即等于弹性应力。即E=σ（e=1），G=τ（e=1）。因此弹性模量是弹性应变为1时的弹性应力。这样的定义从数学关系来看是正确的，但就实际金属来说，因其本身弹性应变极小（一般不超过0.5%），此定义却显得没有意义，也无法按照这种定义去测定。因此在工程上金属弹性模量只能理解为应力应变的比值，表征金属对弹性变形的抗力。它的大小反映了金属材料弹性变形的难易程度，其值越大，则在相同应力下产生的弹性变形就越小。

对于单晶体来说，不同晶向因原子结合力不同其弹性模量也不同，表现为弹性各向异性。常见的体心立方金属和合金，其（111）晶向的弹性模量E₁₁₁为最大，而（100）晶向的弹性模量E₁₀₀为最小，其他晶向的弹性模量E值介于两者之间。多晶体金属各晶粒取向是任意的，其弹性模量应该是各个晶向弹性模量的统计平均值，介于E₁₁₁和E₁₀₀之间。一些常用金属的弹性模量见表2-2。

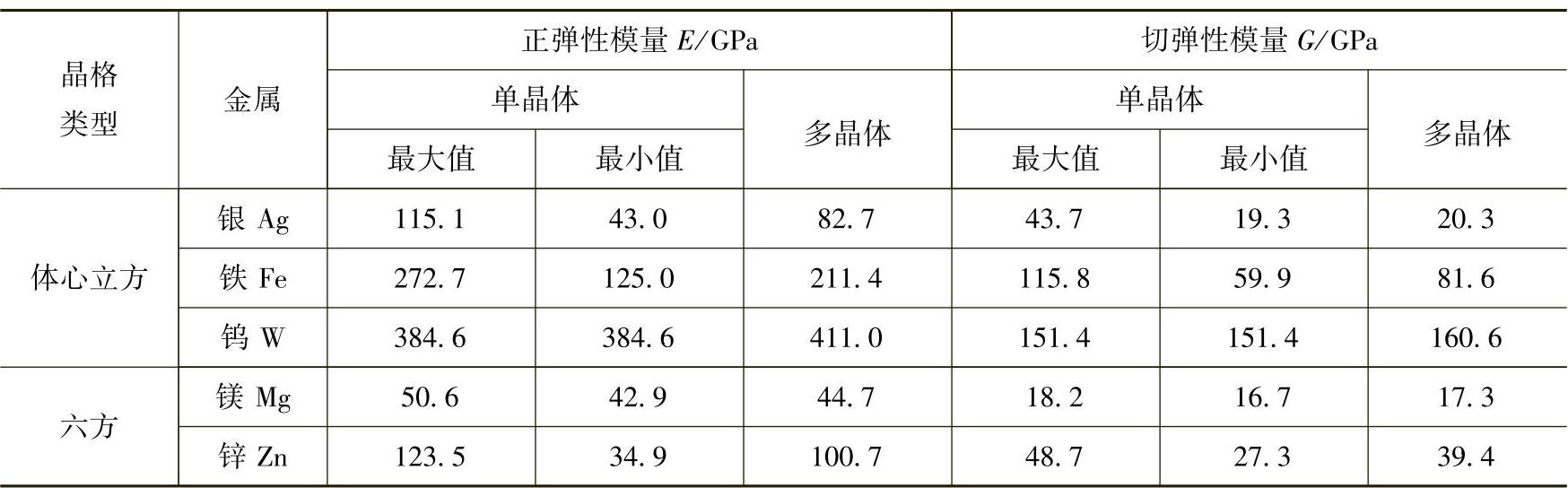
表2-2 一些常用金属的弹性模量

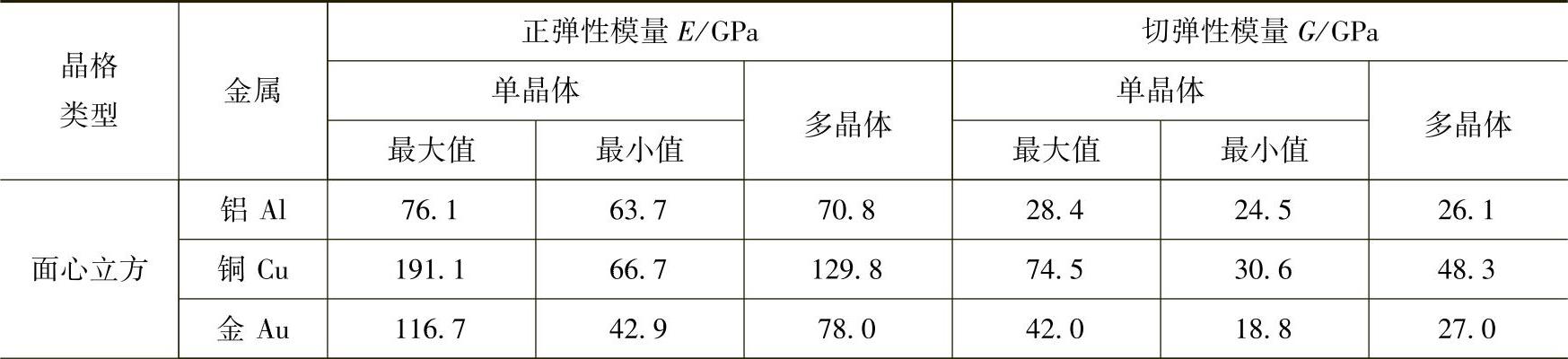
（续）

(www.xing528.com)

绝大部分构件在服役过程中都处于弹性变形状态，其中一些构件要求在一定载荷下只允许产生一定的弹性变形，如镗床的镗杆、机床的主轴、刀架等，如果发生过量的弹性变形就会造成废品。例如，镗杆工作时，若本身发生过量的弹性变形，则镗出的内孔直径就会偏小、有锥度。这就出现了生产中的刚度问题。那么，什么是刚度呢？在工程上往往将构件产生弹性变形的难易程度叫作构件的刚度。拉伸构件的刚度常用ES_o表示，ES_o越大，拉伸构件的弹性变形越小。已知

则

由式（2-19）可知，当零件的长度l_o和外加载荷F一定时，弹性变形的绝对值Δl主要取决于弹性模量E和零件的截面积S_o的乘积ES_o。ES_o值越大，Δl或e值就越小，说明零件就越不容易发生弹性变形，即零件的刚度大。可见要增加零件的刚度，或者是增大零件的截面积S_o，或者是选取E值高的材料。如果零件的截面积不变，则零件的刚度主要取决于材料的E值。所以在设计、选材时，除了设计足够的截面S_o外，还应选用弹性模量高的钢铁材料。所以说E代表了材料刚度的大小，这就是弹性模量的工程技术意义。