近期地貌动态及其影响机制

1.岸线变化数据的提取

根据定义，岸线是水体表面与陆地表面的交叉线，但在实际应用中，由于水体与陆地的边界随着时间和空间的改变而不断地发生变化，根据研究的时空尺度的不同，有一系列不同的指标被用来指示岸线，例如植被线、干湿线和潮汐基准面与海滩剖面的交线等。干湿线等肉眼观测的岸线指标受到观测时间前后潮汐情况的影响较大，随着观测技术的发展和观测数据的积累，基于特定潮位面，例如平均高潮位（Mean High Water）、平均海平面（Mean Sea Level）和平均低潮位（Mean Low Water）等的指示岸线逐渐被广泛使用。由于潮位面在一定的时间尺度内是较为稳定的，这些基于潮位面的指示岸线可以较为精确地从海岸地形观测数据中得到判定和提取，并且不同时间、不同岸段测得的同一指示岸线具有可对比性。

由于海南环岛沿岸的潮差变化较大而平均海平面的高程比较一致，同时为了避免海滩后滨人类活动（如人工护岸、旅游设施等）的直接影响，本研究选取平均海平面与海岸相接的滨线（MSL，0 m等高线）来指示海南环岛的岸线。岸线的位置与岸滩的宽度相关联（如岸线的向海移动意味着岸滩宽度的增加），因此，MSL的水平位置变化可与岸滩平均宽度的变化相联系，并且能够充分反映岸滩地貌动态变化的情况。对同一条垂直于岸线的岸滩剖面，在其后滨取一测量点作为固定参照点，则基于测得的经纬度数据、利用ArcMap[10.1]软件可以计算出各测量点与后滨参照点之间的水平距离，从而得到具有高程和水平距离二维信息的岸滩剖面；因此，高程为0 m的MSL与后滨参照点的水平距离可以简单且精确地从二维剖面中提取。由于后滨参照点的水平位置固定不变，不同时间调查的剖面上高程为0 m的点与后滨参照点的水平距离的变化则代表了该剖面所在海滩的海岸线变化；将环岛各剖面的岸线变化值依次排列，则构成了间隔为5 km的环岛岸线变化的数据序列。

2.岸线变化小波分析

小波变换可以有效地提供时间信号关于频域和时域的信息；对于岸线变化沿岸波动这样的空间数据序列来说，则可以得到不同沿岸尺度下岸线的波动强度（Tebbens，等，2002）。对比传统的傅里叶变换，小波变换在精确解构和重组不连续的和包含尖峰值的有限序列时有明显的优势。本文中对岸线进行的小波分析方法主要基于前人的研究（Malamud和Turcotte，1999；Tebbens，等，2002），具体的计算则通过Matlab R2010a中的Wavelet ToolboxTM模块进行。母小波墨西哥小帽（Mexican Hat）的形式如式（2.1）：

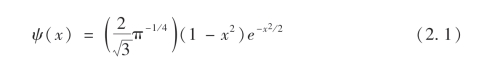
如式（2.2）所示，用小波序列与岸线变化序列f（x）进行卷积：

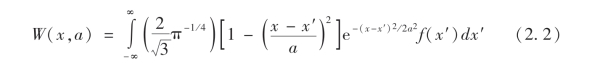
式中的x是自变量，在本研究中代表不同岸滩剖面；a是尺度参数，其决定了与数据序列进行卷积的小波的长度（一般取正整数），结合岸线序列的长度，在保证计算结果有实际意义的前提下，本文中小波变换的尺度参数取值范围为1～16；最终得到不同尺度下各岸滩剖面的小波系数（Wavelet Coefficients）W（x，a）。

因为岸滩剖面是在海南环岛沿岸依次排列的，所以由此得到的岸线变化序列没有真正意义上的起点或终点（N1～N132的命名是为描述方便）。因此，在对岸线变化序列进行小波变换前，对数据序列按顺序进行三次循环排列得到三倍长度的用于小波变换的序列，最后则只取中段的小波系数序列作为结果，因此避免了小波变换边界效应的影响。

3.剖面形态EOF分析

经验正交函数（EOF）分析方法可以用来提取一组数据序列的主要和次要特征；因此在进行EOF分析之前，需要对不同时间、不同岸段监测到的岸滩剖面进行标准化的预处理，以组成用于计算的数据矩阵。首先，将由经纬度和高程组成的剖面信息转化为由水平距离和高程组成的二维剖面，再以MSL为起点、插值成水平距离间隔为1.5 m的标准剖面。为了统一不同剖面之间的长度，较短剖面后滨以上的高程数据用测量的后滨起始点的高程数据补充，此点的高程值通常是剖面上的最高值。其次，对每个调查时间，分别将沿岸方向上连续的多条长度一致的标准剖面进行排列组合，得到用于经验正交函数分析的四个数据矩阵（矩阵的行数由标准剖面的长度决定，列数为参与计算的剖面数量）：一个包含海南环岛所有剖面的矩阵（N1～N132，矩阵列数132），三个包含不同岸段的剖面的矩阵，即东部海岸（N10～N49，矩阵列数40）、南部海岸（N50～N87，矩阵列数38）、西部和北部海岸（N88～N132～N9，矩阵列数54）。因此，通过经验正交函数分析可以得到不同季节、不同海岸区域的岸滩剖面模式，从而进行海南环岛不同岸段的岸滩在不同季节的剖面形态的对比。最后，对各剖面数据矩阵进行经验正交函数分析计算：将矩阵内各数减去其所在行的均值得到距平化处理后的剖面数据矩阵，然后计算其协方差矩阵的特征值和特征向量，以及各个剖面的特征向量权重。每个特征向量的贡献定义为其对应的特征值在所有特征值的总和中所占的百分比，它表示特征向量解释数据集特征的程度。用特征值按降序对特征向量进行排序，即得到最能代表岸滩剖面形态特征的第一特征向量，以及其后的第二特征向量等。

4.岸滩形态及其影响因素的多元回归分析(www.xing528.com)

多元回归模型通过建立因变量与多个自变量之间的拟合方程，判断因变量与各自变量之间的相关关系及其显著性。在本研究中，为了分析对海南岛岸滩形态产生影响的主要因素，分别取岸线变化、体积变化和滩面坡度变化三个参数作为因变量，自变量则包括最大潮差（TR）、水下坡度（SS）、剖面方位角（Azimuth）、期间平均波周期（T）、期间平均波高（Hs）、前30天平均波周期[T（30d）]、前30天平均波高[Hs（30d）]。其中，最大潮差基于TELEMAC流场模型结果（取2013年1—3月期间大潮潮差最大值，模型设置见第四章内容），根据剖面位置选取开敞岸段剖面水下5 m处为潮汐提取点，提取期间最大潮差作为剖面所在岸段潮差情况的一个常数值，旨在区别不同剖面的潮汐作用。波浪数据来源于欧洲中期天气预报中心的全球再分析数据ERA-Interim，网格精度为0.125°×0.125°，时间精度为6 h（即一天4个时刻，00：00、06：00、12：00、18：00），数据包括有效波高（风浪和涌浪，Significant Height of Combined Wind Waves and Swell）、平均浪向（Mean Wave Direction）和平均波周期（Mean Wave Period）。ECMWF ERA-Interim的波浪参数利用ERS-1、ERS-2、ENVISAT和Jason-1卫星雷达高度计的波高观测结果进行同化；基于从浮标、平台和气象船获得的经过质量控制的海面波浪参数的实地观测资料，对ERAInterim数据进行验证的结果显示，ERA-Interim的波浪数据中Hs的离散指数（再分析数据与实测数据差值的归一化标准偏差）为16%～20%、偏差（平均再分析值与实测值之差）为-0.05～0.00 m，Tp的离散指数为16%～24%、偏差为0.0～0.3 s（Deea，等，2011）；ERA-Interim波浪数据的精度基本能满足本研究的分析需求。由于各剖面所处位置、水下地形各不相同，波浪传入近岸区域发生的折绕射和能量消减情况也不尽相同；因此统计各岸段的波浪条件时主要考虑水深大于20 m的深水波浪情况。根据海南环岛的地形，以海湾为单元选取一个水深大于20 m的波浪数据点，其统计结果代表此海湾的波浪情况。由于海南岛沿岸的波浪方向和高度年内变化主要发生在4月和9月，因此，夏季和冬季的海滩调查结果可能受到季节性波浪条件的控制，也可能受到两次调查之间整体动力情况的影响，例如台风。因此，在建立多元回归模型时对波浪条件采用了两种统计区间：一是两次调查之间的平均波况；二是后一次调查的前30天平均波况。夏季-冬季和冬季-夏季的波浪统计结果如图2-3所示，对各次调查所统计波浪数据的时间区间见表2-2（前30天表示后一次调查开始前30天的波浪统计情况）。

表2-2　多元回归模型中使用的波浪数据对应的统计时间区间

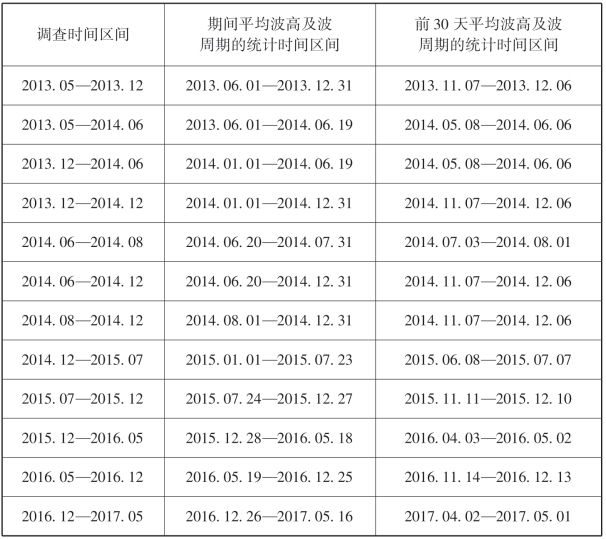
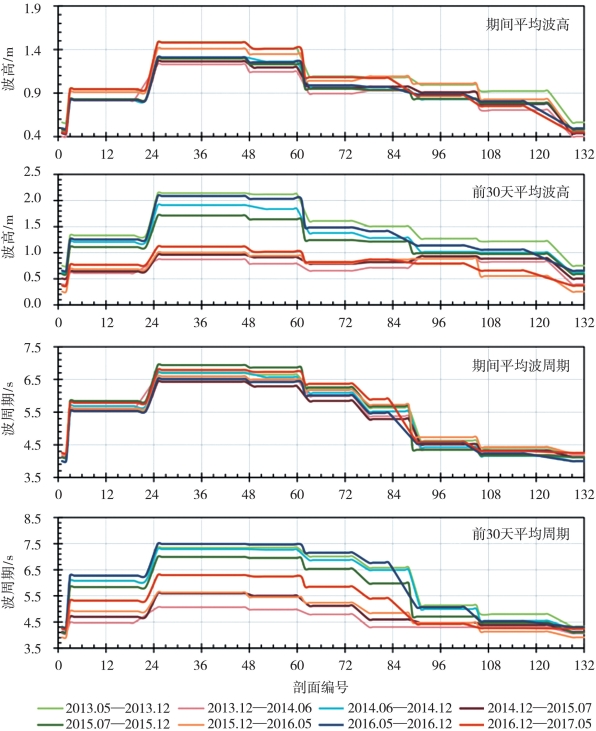
图2-3　多元回归分析所使用的夏季-冬季和冬季-夏季环岛波浪统计数据

其他自变量和因变量的取值和计算方法如下。

①水下坡度：根据海图提取各剖面处岸线至-5 m水深位置的坡度。

②滩面坡度：岸滩剖面高程0 m位置至向陆水平距离10 m处的坡度。

③岸线变化：岸滩剖面上0 m等高线位置的水平变化。

④海滩体积：岸滩剖面0 m等高线以上的曲线积分，即海滩的单宽体积。

⑤剖面方位角：根据岸滩剖面走向的经纬度计算得到的方位角。

海岸的坡度不仅是地貌动态变化的特征形态之一，而且也影响着海岸与水动力环境的相互作用情况（Jackson，等，2005；Pardo-Pascual，等，2014）。在本研究中，将海岸坡度分为两部分，即水下坡度和滩面坡度，其中水下坡度基于海图，视作剖面的固定参数、不随调查时间变化，滩面坡度则根据岸滩剖面监测数据计算，随着剖面形态的变化而变化。因为岸滩剖面与局部岸线呈垂向相交，参数方位角可以指代局部岸线的朝向，作为固定参数。