高等数学练习题5-4参考解答及分析

1.【分析】 （1）利用分布列规范性的性质可得a=0.4

P{ξ＜2}=P{ξ=-2}+P{ξ=0}=0.1+0.3=0.4

（2）E（ξ）=（-2）×0.1+0×0.3+2×0.4+3×0.2=1.2

D（ξ）=（-2-1.2）2×0.1+（0-1.2）2×0.3+（2+1.2）2×0.4

+（3-1.2）2×0.2=2.36

2.【分析】 首先比较E（ξ₁）和E（ξ₂），若E（ξ₁）=E（ξ₂），再比较D（ξ₁）与D（ξ₂）

E（ξ₁）=8×0.4+9×0.1+10×0.5=9.1

E（ξ₂）=8×0.3+9×0.5+10×0.2=8.9

所以甲比乙发挥得更稳定.

3.【分析】 首先要知道ξ的取值并算出取这些值时的概率.

因为只有4个红球，所以取到白球的次数可能是1，2，3，4，5.因此，ξ的取值为1，2，3，4，5.所以

2.【分析】 首先比较E（ξ₁）和E（ξ₂），若E（ξ₁）=E（ξ₂），再比较D（ξ₁）与D（ξ₂）

E（ξ₁）=8×0.4+9×0.1+10×0.5=9.1

E（ξ₂）=8×0.3+9×0.5+10×0.2=8.9

所以甲比乙发挥得更稳定.

3.【分析】 首先要知道ξ的取值并算出取这些值时的概率.

因为只有4个红球，所以取到白球的次数可能是1，2，3，4，5.因此，ξ的取值为1，2，3，4，5.所以

2.【分析】 首先比较E（ξ₁）和E（ξ₂），若E（ξ₁）=E（ξ₂），再比较D（ξ₁）与D（ξ₂）

E（ξ₁）=8×0.4+9×0.1+10×0.5=9.1

E（ξ₂）=8×0.3+9×0.5+10×0.2=8.9

所以甲比乙发挥得更稳定.

3.【分析】 首先要知道ξ的取值并算出取这些值时的概率.

因为只有4个红球，所以取到白球的次数可能是1，2，3，4，5.因此，ξ的取值为1，2，3，4，5.所以

类似地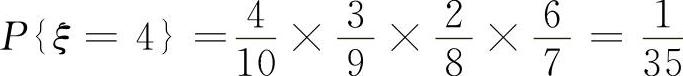

类似地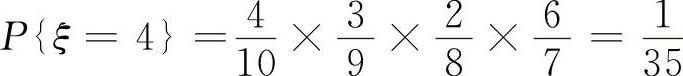

类似地 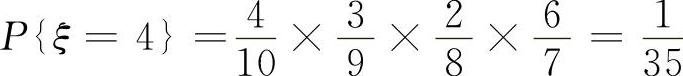(www.xing528.com)

所以ξ的分布列为

所以ξ的分布列为

所以ξ的分布列为

4.【分析】 根据分布函数的定义可知

当x＜1时，F（x）=0.

1≤x＜2时，F（x）=0.3.

2≤x＜3时，F（x）=0.3+0.5=0.8.

x≥3时，F（x）=0.3+0.5+0.2=1.

4.【分析】 根据分布函数的定义可知

当x＜1时，F（x）=0.

1≤x＜2时，F（x）=0.3.

2≤x＜3时，F（x）=0.3+0.5=0.8.

x≥3时，F（x）=0.3+0.5+0.2=1.

4.【分析】 根据分布函数的定义可知

当x＜1时，F（x）=0.

1≤x＜2时，F（x）=0.3.

2≤x＜3时，F（x）=0.3+0.5=0.8.

x≥3时，F（x）=0.3+0.5+0.2=1.

所以，F（1.5）=0.3.

所以，F（1.5）=0.3.

所以，F（1.5）=0.3.

5.【分析】 由分布函数F（x）可知ξ的可能取值为-1，0，1，2.而函数F（x）在间断点x=-1处的跃度为0.2，在x=0处的跃度为0.5-0.2=0.3，在点x=1和x=2处的跃度分别为0.9-0.5=0.4和1-0.9=0.1.所以ξ的分布列为

5.【分析】 由分布函数F（x）可知ξ的可能取值为-1，0，1，2.而函数F（x）在间断点x=-1处的跃度为0.2，在x=0处的跃度为0.5-0.2=0.3，在点x=1和x=2处的跃度分别为0.9-0.5=0.4和1-0.9=0.1.所以ξ的分布列为

5.【分析】 由分布函数F（x）可知ξ的可能取值为-1，0，1，2.而函数F（x）在间断点x=-1处的跃度为0.2，在x=0处的跃度为0.5-0.2=0.3，在点x=1和x=2处的跃度分别为0.9-0.5=0.4和1-0.9=0.1.所以ξ的分布列为