1.选D选项.
【分析】 由于只有4件次品,因此一次取5件产品中,至少有1件是正品的事件是必然发生的,所以选D选项.
2.选C选项.
【分析】 由于A,B互不相容,即AB=∅.利用对偶律:
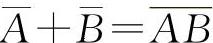 ,因此
,因此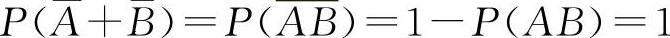 ,选C选项.当A,B为对立事件时显然有P(AB)≠0,对于P(AB)=0不一定能得到P(A)=0或P(B)=0,如掷一枚硬币A=“正面向上”,B=“反面向上”,显然P(AB)=0,但
,选C选项.当A,B为对立事件时显然有P(AB)≠0,对于P(AB)=0不一定能得到P(A)=0或P(B)=0,如掷一枚硬币A=“正面向上”,B=“反面向上”,显然P(AB)=0,但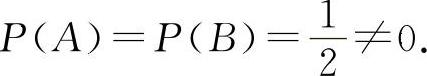 而互不相容的A与B虽有AB=∅但不一定A+B=Ω,所以选项D也不正确.所以选C选项.
而互不相容的A与B虽有AB=∅但不一定A+B=Ω,所以选项D也不正确.所以选C选项.
3.选B选项.
【分析】A,B互斥,即AB=∅,而P(A+B)=P(A)+P(B)-P(AB)所以P(A+B)=P(A)+P(B),得P(B)=0.4,所以选B选项.
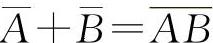 ,因此
,因此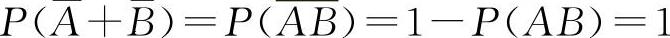 ,选C选项.当A,B为对立事件时显然有P(AB)≠0,对于P(AB)=0不一定能得到P(A)=0或P(B)=0,如掷一枚硬币A=“正面向上”,B=“反面向上”,显然P(AB)=0,但
,选C选项.当A,B为对立事件时显然有P(AB)≠0,对于P(AB)=0不一定能得到P(A)=0或P(B)=0,如掷一枚硬币A=“正面向上”,B=“反面向上”,显然P(AB)=0,但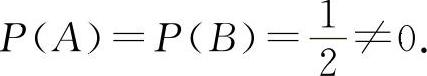 而互不相容的A与B虽有AB=∅但不一定A+B=Ω,所以选项D也不正确.所以选C选项.
而互不相容的A与B虽有AB=∅但不一定A+B=Ω,所以选项D也不正确.所以选C选项.
3.选B选项.
【分析】A,B互斥,即AB=∅,而P(A+B)=P(A)+P(B)-P(AB)所以P(A+B)=P(A)+P(B),得P(B)=0.4,所以选B选项.
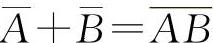 ,因此
,因此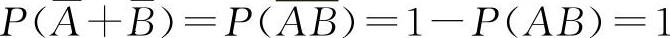 ,选C选项.当A,B为对立事件时显然有P(AB)≠0,对于P(AB)=0不一定能得到P(A)=0或P(B)=0,如掷一枚硬币A=“正面向上”,B=“反面向上”,显然P(AB)=0,但
,选C选项.当A,B为对立事件时显然有P(AB)≠0,对于P(AB)=0不一定能得到P(A)=0或P(B)=0,如掷一枚硬币A=“正面向上”,B=“反面向上”,显然P(AB)=0,但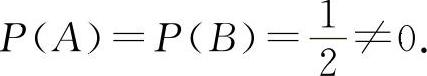 而互不相容的A与B虽有AB=∅但不一定A+B=Ω,所以选项D也不正确.所以选C选项.
而互不相容的A与B虽有AB=∅但不一定A+B=Ω,所以选项D也不正确.所以选C选项.
3.选B选项.
【分析】A,B互斥,即AB=∅,而P(A+B)=P(A)+P(B)-P(AB)所以P(A+B)=P(A)+P(B),得P(B)=0.4,所以选B选项.
4.应填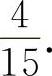
4.应填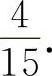
4.应填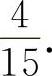
【分析】 因为是依次选取,所以样本空间的基本事件为C110×C19,甲抽选择题,乙抽判断题的基本事件分别为C16与C41,所以其概率为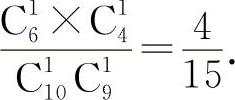
【分析】 因为是依次选取,所以样本空间的基本事件为C110×C19,甲抽选择题,乙抽判断题的基本事件分别为C16与C41,所以其概率为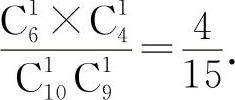 (https://www.xing528.com)
(https://www.xing528.com)
【分析】 因为是依次选取,所以样本空间的基本事件为C110×C19,甲抽选择题,乙抽判断题的基本事件分别为C16与C41,所以其概率为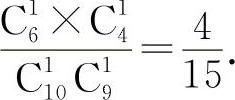
5.【分析】 1,2,3之和为6的是三个数只能是1+2+3=6或2+2+2=6,由于号码的顺序不同是不同的样本点,所以样本空间的基本事件是3!+1=7个,写出来是Ω={(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1),(2,2,2)},所以三个2的基本事件只有一个,故设A=“三次取到的都是2号球”,则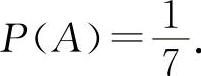
6.【分析】 样本空间的基本事件数共C15×A25个,其中C15是百位数不为0的取法,而十位与个位为A25种取法.
5.【分析】 1,2,3之和为6的是三个数只能是1+2+3=6或2+2+2=6,由于号码的顺序不同是不同的样本点,所以样本空间的基本事件是3!+1=7个,写出来是Ω={(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1),(2,2,2)},所以三个2的基本事件只有一个,故设A=“三次取到的都是2号球”,则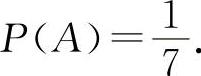
6.【分析】 样本空间的基本事件数共C15×A25个,其中C15是百位数不为0的取法,而十位与个位为A25种取法.
5.【分析】 1,2,3之和为6的是三个数只能是1+2+3=6或2+2+2=6,由于号码的顺序不同是不同的样本点,所以样本空间的基本事件是3!+1=7个,写出来是Ω={(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1),(2,2,2)},所以三个2的基本事件只有一个,故设A=“三次取到的都是2号球”,则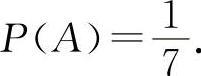
6.【分析】 样本空间的基本事件数共C15×A25个,其中C15是百位数不为0的取法,而十位与个位为A25种取法.
3位数是奇数:个位数的取法C13,百位数的取法C14.十位数的取法仍在剩下的4个数中取一个:C14,所以共有C13×C14×C14,设A=“3位数为奇数”,则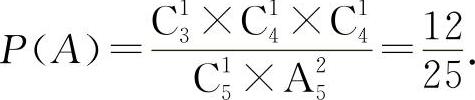
7.【分析】 每一个人的出生月份有12种可能,则5个团员共有125.这就是样本空间的基本事件总数.
3位数是奇数:个位数的取法C13,百位数的取法C14.十位数的取法仍在剩下的4个数中取一个:C14,所以共有C13×C14×C14,设A=“3位数为奇数”,则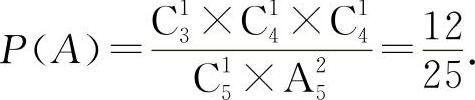
7.【分析】 每一个人的出生月份有12种可能,则5个团员共有125.这就是样本空间的基本事件总数.
3位数是奇数:个位数的取法C13,百位数的取法C14.十位数的取法仍在剩下的4个数中取一个:C14,所以共有C13×C14×C14,设A=“3位数为奇数”,则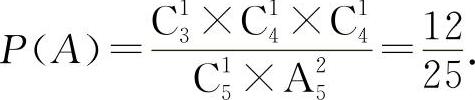
7.【分析】 每一个人的出生月份有12种可能,则5个团员共有125.这就是样本空间的基本事件总数.
5个人出生的月份都不同相当于从12个月份中选出5个月份的排列,即A512(种).若设A=“5个团员出生的月份都不同”,则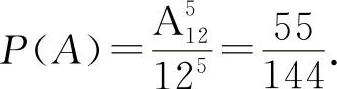
5个人出生的月份都不同相当于从12个月份中选出5个月份的排列,即A512(种).若设A=“5个团员出生的月份都不同”,则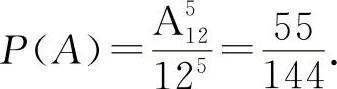
5个人出生的月份都不同相当于从12个月份中选出5个月份的排列,即A512(种).若设A=“5个团员出生的月份都不同”,则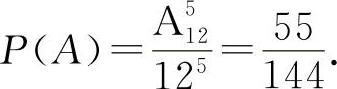
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




