2.【分析】利用函数的对应法则可得
f(x-y,x+y)=[(x-y)(x+y)](x-y)+(x+y)=(x2-y2)2x
3.因为 f(x-y,xy)=(x-y)3+3x2y-3xy2-3xy=(x-y)3+3xy(x-y-1)
所以 f(x,y)=x3+3(x-1)y
4.应选C选项 【分析】
因为 f(x+y,xy)=(x+y)2-2xy-(xy)3
所以 f(x,y)=x2-2y-y3
2.【分析】利用函数的对应法则可得
f(x-y,x+y)=[(x-y)(x+y)](x-y)+(x+y)=(x2-y2)2x
3.因为 f(x-y,xy)=(x-y)3+3x2y-3xy2-3xy=(x-y)3+3xy(x-y-1)
所以 f(x,y)=x3+3(x-1)y
4.应选C选项 【分析】
因为 f(x+y,xy)=(x+y)2-2xy-(xy)3
所以 f(x,y)=x2-2y-y3
2.【分析】利用函数的对应法则可得
f(x-y,x+y)=[(x-y)(x+y)](x-y)+(x+y)=(x2-y2)2x
3.因为 f(x-y,xy)=(x-y)3+3x2y-3xy2-3xy=(x-y)3+3xy(x-y-1)
所以 f(x,y)=x3+3(x-1)y
4.应选C选项 【分析】
因为 f(x+y,xy)=(x+y)2-2xy-(xy)3
所以 f(x,y)=x2-2y-y3
则有 
则有 
则有 
5.应填 【分析】 z对y求偏导数时应该用幂函数的求导公式
【分析】 z对y求偏导数时应该用幂函数的求导公式
5.应填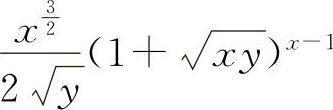 【分析】 z对y求偏导数时应该用幂函数的求导公式
【分析】 z对y求偏导数时应该用幂函数的求导公式
5.应填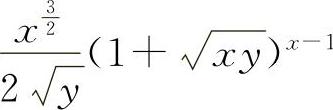 【分析】 z对y求偏导数时应该用幂函数的求导公式
【分析】 z对y求偏导数时应该用幂函数的求导公式
6.解 (1)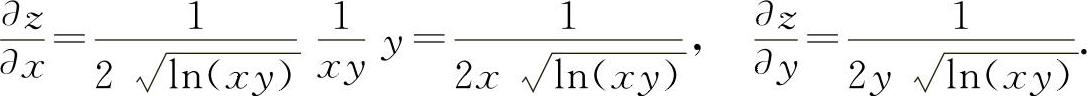
6.解 (1)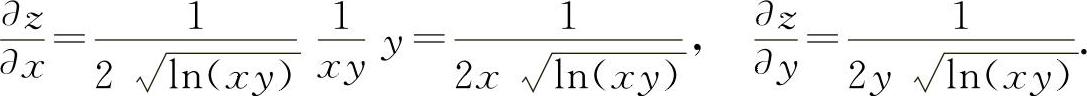
6.解 (1)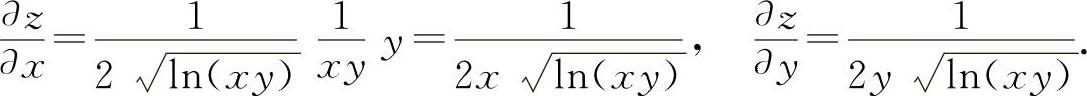
(2)【分析】 此时函数z是x的幂指函数,与题5中求 时的z是y的幂函数有很大区别.考生可用一元函数中的对数求导法,也可用多元复合函数求导公式.
时的z是y的幂函数有很大区别.考生可用一元函数中的对数求导法,也可用多元复合函数求导公式.
解法一 对数求导法
将等式两边取对数得 lnz=xln(1+xy)
(2)【分析】 此时函数z是x的幂指函数,与题5中求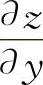 时的z是y的幂函数有很大区别.考生可用一元函数中的对数求导法,也可用多元复合函数求导公式.
时的z是y的幂函数有很大区别.考生可用一元函数中的对数求导法,也可用多元复合函数求导公式.
解法一 对数求导法
将等式两边取对数得 lnz=xln(1+xy)
(2)【分析】 此时函数z是x的幂指函数,与题5中求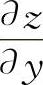 时的z是y的幂函数有很大区别.考生可用一元函数中的对数求导法,也可用多元复合函数求导公式.
时的z是y的幂函数有很大区别.考生可用一元函数中的对数求导法,也可用多元复合函数求导公式.
解法一 对数求导法
将等式两边取对数得 lnz=xln(1+xy)
两边对x求导得 
两边对x求导得 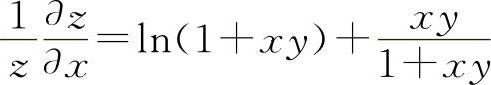
两边对x求导得 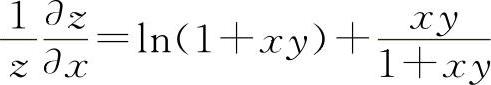
所以 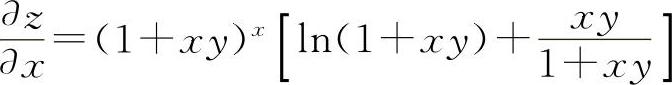
解法二 复合函数求导法
设u=1+xy,v=x,则z=uv.
所以 
解法二 复合函数求导法
设u=1+xy,v=x,则z=uv.
所以 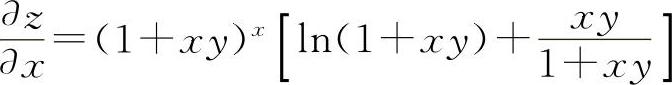
解法二 复合函数求导法
设u=1+xy,v=x,则z=uv.
则 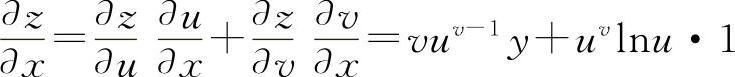
则 
则 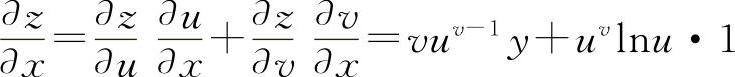
7.【分析】 用复合函数求导公式分别求出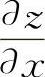 与
与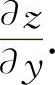
解 设z=uv,其中u=x2+y2,v=xy.
7.【分析】 用复合函数求导公式分别求出 与
与
解 设z=uv,其中u=x2+y2,v=xy.
7.【分析】 用复合函数求导公式分别求出 与
与
解 设z=uv,其中u=x2+y2,v=xy.
则 
则 
则 
注 如果z=f(x,y),将x与y的位置互换,所得到的函数与z相等,即z=f(x,y)=f(y,x),这样的函数称为对称函数.对称函数在求偏导时,可以利用对称性.如本题z=(x2+y2)xy就是对称函数,求出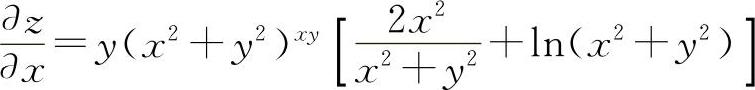 后,则求
后,则求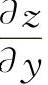 时只需利用对称性,将
时只需利用对称性,将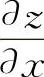 中的x换成y,y换成x就得到结果
中的x换成y,y换成x就得到结果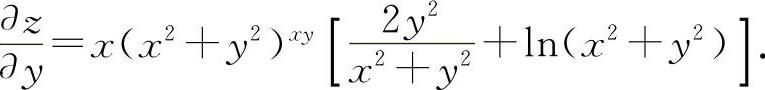
由于对称函数在求偏导时用得比较多,而且此方法易记忆,且使用简单,故介绍给考生.例
注 如果z=f(x,y),将x与y的位置互换,所得到的函数与z相等,即z=f(x,y)=f(y,x),这样的函数称为对称函数.对称函数在求偏导时,可以利用对称性.如本题z=(x2+y2)xy就是对称函数,求出 后,则求
后,则求 时只需利用对称性,将
时只需利用对称性,将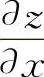 中的x换成y,y换成x就得到结果
中的x换成y,y换成x就得到结果
由于对称函数在求偏导时用得比较多,而且此方法易记忆,且使用简单,故介绍给考生.例
注 如果z=f(x,y),将x与y的位置互换,所得到的函数与z相等,即z=f(x,y)=f(y,x),这样的函数称为对称函数.对称函数在求偏导时,可以利用对称性.如本题z=(x2+y2)xy就是对称函数,求出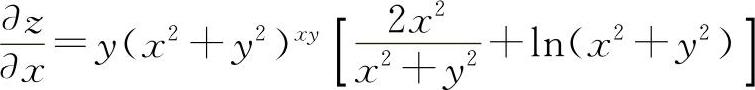 后,则求
后,则求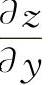 时只需利用对称性,将
时只需利用对称性,将 中的x换成y,y换成x就得到结果
中的x换成y,y换成x就得到结果
由于对称函数在求偏导时用得比较多,而且此方法易记忆,且使用简单,故介绍给考生.例
如,例8中的(1)为对称函数,求出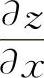 后,可立即写出
后,可立即写出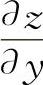 ,从而得到结果.
,从而得到结果.
如,例8中的(1)为对称函数,求出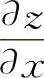 后,可立即写出
后,可立即写出 ,从而得到结果.
,从而得到结果.
如,例8中的(1)为对称函数,求出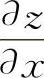 后,可立即写出
后,可立即写出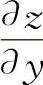 ,从而得到结果.
,从而得到结果.
8.解 对x求导得
8.解 对x求导得
8.解 对x求导得
对y求导得  (https://www.xing528.com)
(https://www.xing528.com)
对y求导得 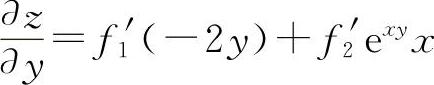
对y求导得 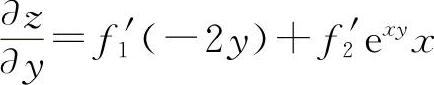
所以 
所以 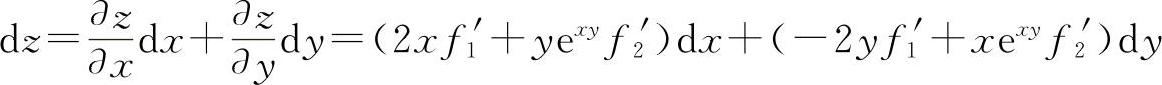
所以 
9.解 对x求导得 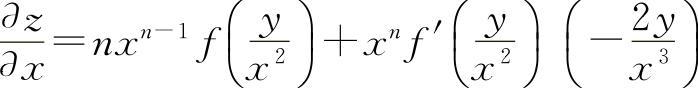
9.解 对x求导得 
9.解 对x求导得 
对y求导得 
对y求导得 
对y求导得 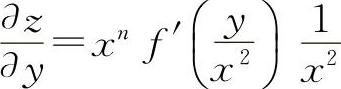
因此 
因此 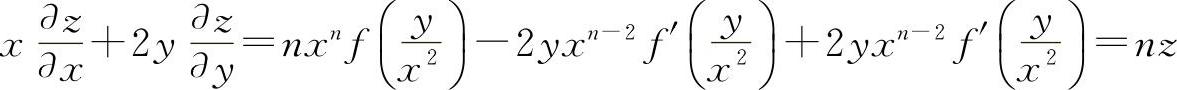
因此 
10.解 (1)设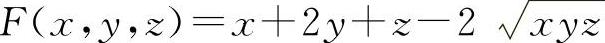
10.解 (1)设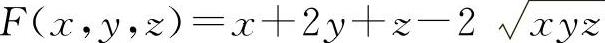
10.解 (1)设
则 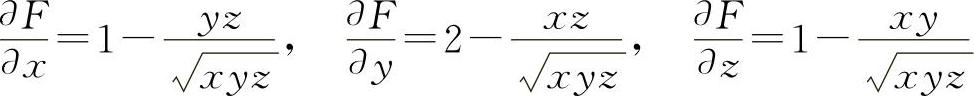
则 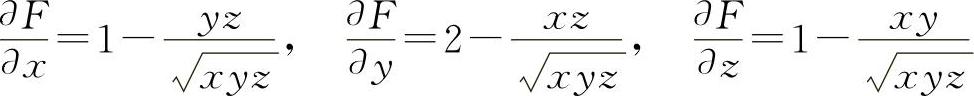
则 
所以 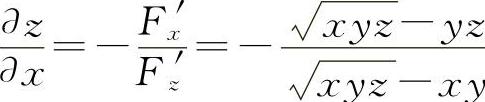 ,
,
(2)设F(x,y,z)=x2+z2-lnz+lny
所以  ,
,
(2)设F(x,y,z)=x2+z2-lnz+lny
所以 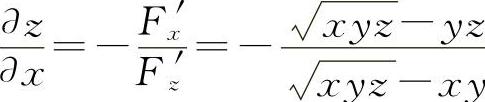 ,
,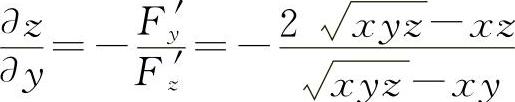
(2)设F(x,y,z)=x2+z2-lnz+lny
则  ,
,  ,
, 
则 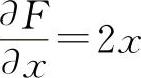 ,
,  ,
, 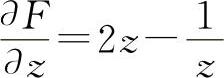
则  ,
, 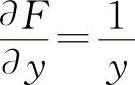 ,
, 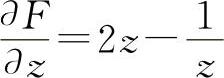
所以 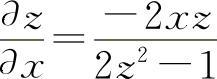 ,
,
(3)设F(x,y,z)=x+y+z-e-(x+y+z)
所以 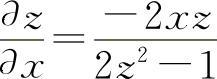 ,
,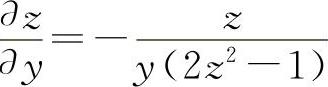
(3)设F(x,y,z)=x+y+z-e-(x+y+z)
所以  ,
,
(3)设F(x,y,z)=x+y+z-e-(x+y+z)
则  ,
,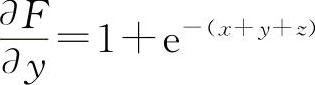 ,
,
则  ,
,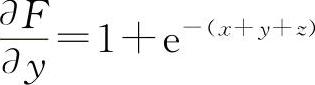 ,
,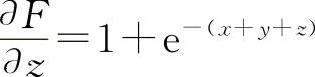
则 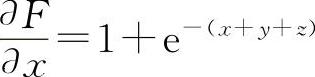 ,
,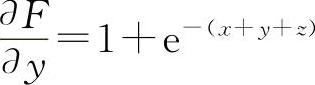 ,
,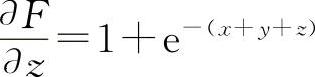
所以  ,
,
所以  ,
,
所以  ,
,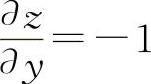
11.解 先求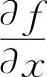 与
与 ,分别令
,分别令 与
与 可得
可得
11.解 先求 与
与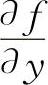 ,分别令
,分别令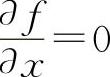 与
与 可得
可得
11.解 先求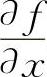 与
与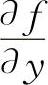 ,分别令
,分别令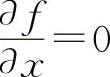 与
与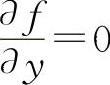 可得
可得
解此方程组得可能的极值点为x=-6,y=-3.
又因为A=fx″x(-6,-3)=1,B=fx″y(-6,-3)=-1,C=fy″y(-6,-3)=2.
则有 B2-AC=-1<0,且A=1>0
所以函数f(x,y)在点(-6,-3)有极小值,极小值为
f(-6,-3)=-9
12.【分析】 构造拉格朗日函数求解.
解 设F(x,y,λ)=x2+y2+λ(2x+y-5)
则
解此方程组得可能的极值点为x=-6,y=-3.
又因为A=fx″x(-6,-3)=1,B=fx″y(-6,-3)=-1,C=fy″y(-6,-3)=2.
则有 B2-AC=-1<0,且A=1>0
所以函数f(x,y)在点(-6,-3)有极小值,极小值为
f(-6,-3)=-9
12.【分析】 构造拉格朗日函数求解.
解 设F(x,y,λ)=x2+y2+λ(2x+y-5)
则
解此方程组得可能的极值点为x=-6,y=-3.
又因为A=fx″x(-6,-3)=1,B=fx″y(-6,-3)=-1,C=fy″y(-6,-3)=2.
则有 B2-AC=-1<0,且A=1>0
所以函数f(x,y)在点(-6,-3)有极小值,极小值为
f(-6,-3)=-9
12.【分析】 构造拉格朗日函数求解.
解 设F(x,y,λ)=x2+y2+λ(2x+y-5)
则
由①和②得x=2y代入③得y=1,x=2,所以f(2,1)=5为极值.
由于点(0,5)满足约束条件2x+y-5=0,且f(0,5)=25>f(2,1)=5,所以f(2,1)=5为极小值.
由①和②得x=2y代入③得y=1,x=2,所以f(2,1)=5为极值.
由于点(0,5)满足约束条件2x+y-5=0,且f(0,5)=25>f(2,1)=5,所以f(2,1)=5为极小值.
由①和②得x=2y代入③得y=1,x=2,所以f(2,1)=5为极值.
由于点(0,5)满足约束条件2x+y-5=0,且f(0,5)=25>f(2,1)=5,所以f(2,1)=5为极小值.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




