高等数学：偏导数与全微分

1.偏导数的定义

定义 设函数z=f（x，y）在点（x₀，y₀）的某个邻域内有定义，当自变量x在x₀处取得改变量Δx（Δx≠0），而y=y₀保持不变时，得到一个改变量

Δ_xz=f（x₀=Δx，y₀）-f（x₀，y₀）

如果当Δx→0时，极限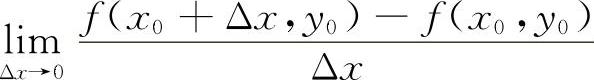

存在，则称此极限值为函数f（x，y）在点（x₀，y₀）处对x的偏导数，记作

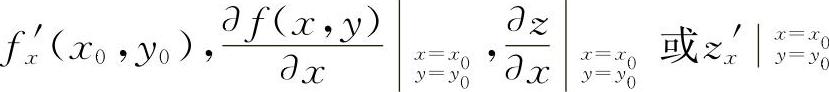
同理可以定义f（x，y）对y的偏导数，即如果极限

存在，则称此极限值为函数f（x，y）在点（x₀，y₀）处对y的偏导数，记作

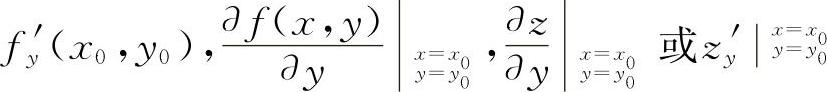
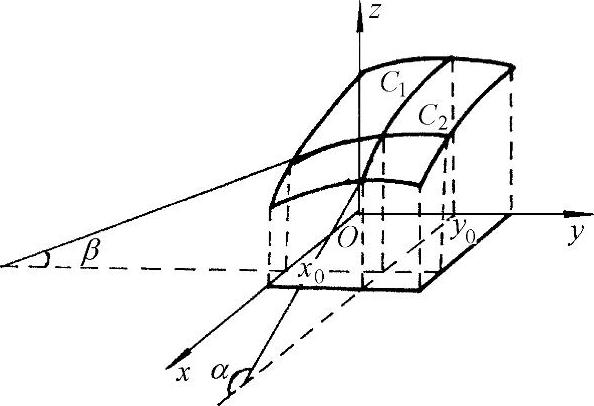
图 4-1

2.偏导数的几何意义

二元函数z=f（x，y）在点（x₀，y₀）处对x的偏导数的几何意义是：在曲面z=f（x，y）与平面y=y₀相交的曲线C₁，即在曲线z=f（x，y₀）上，过点（x₀，y₀）所做切线的斜率tanα（如图4-1所示）.

同理，二元函数z=f（x，y）在点（x₀，y₀）处对y的偏导数的几何意义是：在曲面z=f（x，y）与平面x=x₀相交的曲线C₂，即z=f（x₀，y）上，过点（x₀，y₀）所做切线的斜率tanβ.

设二元函数z=f（x，y）在区域D内每一点（x，y）处都有偏导数f_x'（x，y），f_y'（x，y），一般说来，它们是（x，y）的函数，称为f（x，y）的偏导函数，通常简称为偏导数，记作

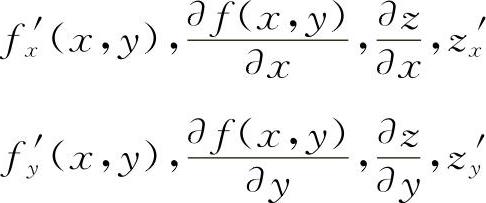
类似地可以定义三元函数u=f（x，y，z）对x，y，z的偏导数f_x'（x，y，z），f_y'（x，y，z），f_z'（x，y，z）.

3.偏导数的求法

设二元函数为z=f（x，y）.(www.xing528.com)

当求f（x，y）对x的偏导数时，只要将二元函数中的y看成常数，而对x求导数即可.同理，求f（x，y）对y的偏导数时，要将x看成常数，而对y求导数.这样求出的是偏导函数，如果要求函数f（x，y）在点（x₀，y₀）处的偏导数，只需在偏导函数中将x=x₀，y=y₀代入即可.

三元函数u=f（x，y，z）对x，y，z的偏导数的定义与求法与此类似.

4.全微分的概念

定义 对于自变量在点（x，y）处的改变量Δx，Δy，如果函数z=f（x，y）的全改变量

Δz=f（x+Δx，y+Δy）-f（x，y）可以表示为

Δz=AΔx+BΔy+o（ρ）其中，A、B与Δx、Δy无关，可能是x、y的函数，o（ρ）是比ρ较高阶的无穷小量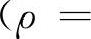，则称AΔx+BΔy是函数z=f（x，y）在点（x，y）处的全微分，记作

dz=df（x，y）=AΔx+BΔy并称函数z=f（x，y）在点（x，y）处可微.

有了函数z=f（x，y）可微与全微分的定义之后，以下的问题就是：二元函数满足什么条件就可微？其中的A与B的值如何求出？

回答这个问题，有以下的定理.

定理4.1 如果函数z=f（x，y）在点（x，y）的某一邻域内存在连续的一阶偏导数f_x'（x，y），f_y'（x，y），则函数z=f（x，y）在点（x，y）处可微，且

dz=f_x'（x，y）dx+f_y'（x，y）dy

5.全微分的求法

求z=f（x，y）的全微分的表达式时，先求出两个一阶偏导数，然后代入上式即可.若要计算全微分的值，则要将x₀，y₀的值代入，并将dx用Δx、dy用Δy的值代入.

6.二阶偏导数

一般地，二元函数z=f（x，y）的偏导数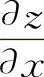，仍是x，y的二元函数，如果这两个函数关于x，y的偏导数也存在，则称它们为z=f（x，y）的二阶偏导数.

例如，函数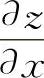再对x求偏导数，即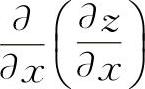是z=f（x，y）的一个二阶偏导数，记为 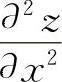，显然关于二元函数z=f（x，y）的二阶偏导数共有4种，即

称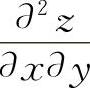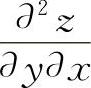，为z=f（x，y）的二阶混合偏导数.

注意：一般地，两个二阶混合偏导数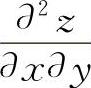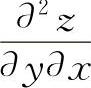，不一定相等.但是，当它们都是x，y的连续函数时，则两个混合偏导数相等，即求函数z=f（x，y）关于x，y的二阶混合偏导数时，次序可以交换.