高等数学章五练习题3-3参考解答及分析

1.【分析】 求已知曲线围成的平面图形的面积一般分三步：

首先画出每一条曲线的图像，然后求其交点，以便确定积分限.第三步再求其面积.

解 （1）画出y=x²与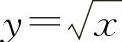的图像如图3-14所示，解方程组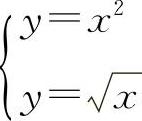，得交点（0，0）和（1，1），

则其面积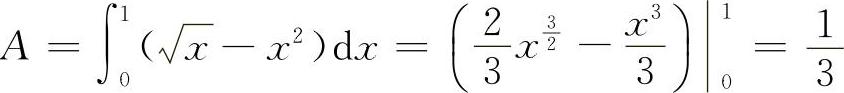

（2）画出已知曲线所围成区域的平面图形如图3-15所示.解方程组

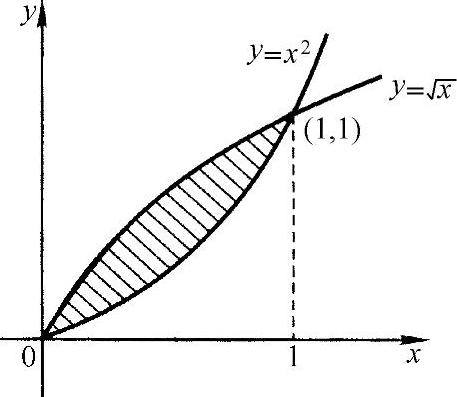
图 3-14

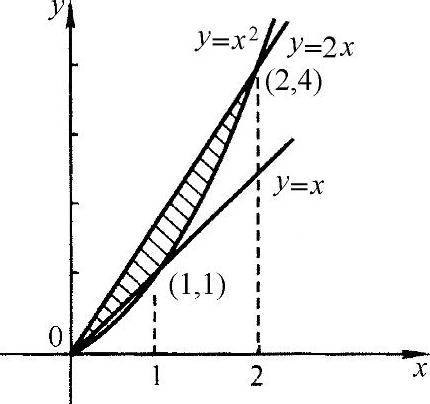
图 3-15

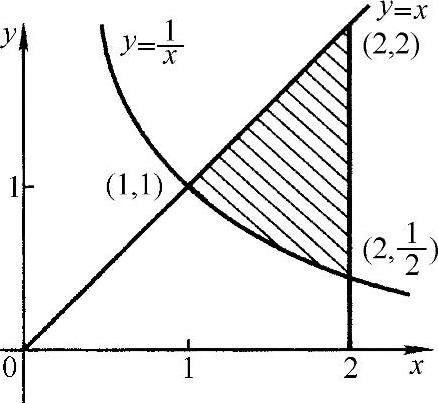
图 3-16

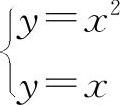与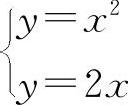，分别得交点（0，0），（1，1）和（0，0），（2，4）.

则其面积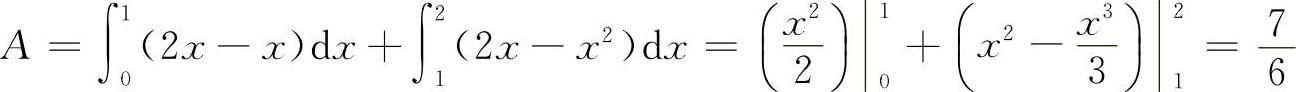

（3）画出的平面图形如图3-16所示.求得的交点为（1，1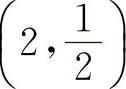），，（2，2），则有平面图形的面积

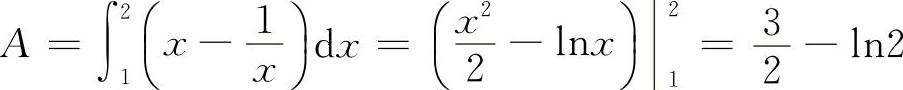
（4）画出平面图形如图3-17所示.求得的交点为（0，0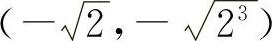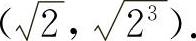），，由于

图形面积是对称的，所以其面积

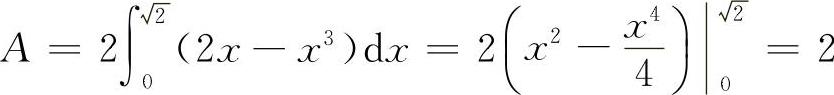
2.【分析】 先求切线方程，再画平面图形.

解因为y'=-2x+4，所以y'（0）=4，y'（3）=-2，所以过点（0，-3）的切线方程为y=4x-3，过点（3，0）的切线方程为y=-2x+6，两切线的交点为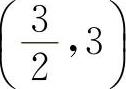，画出平面图形如图3-18所示，所以

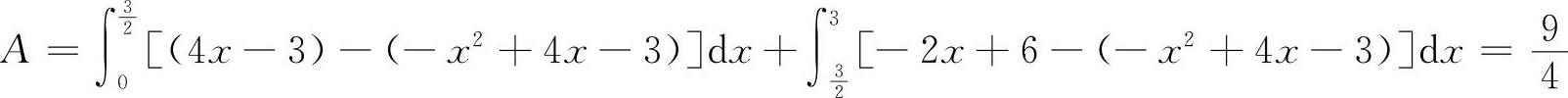
3.【分析】 先求y²=4x在点（1，2）的切线斜率，然后求出在点（1，2）处的法线方程，并画出平面图形，求出其交点的坐标并计算平面图形的面积.

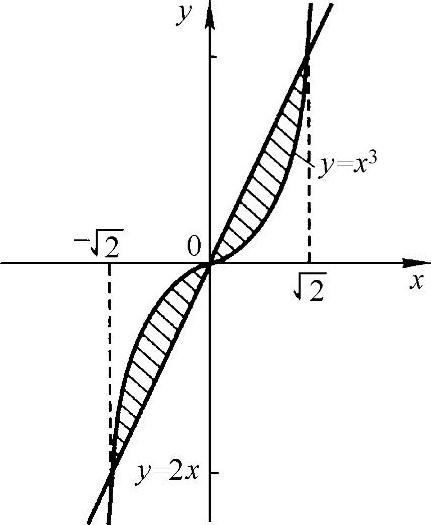
图 3-17

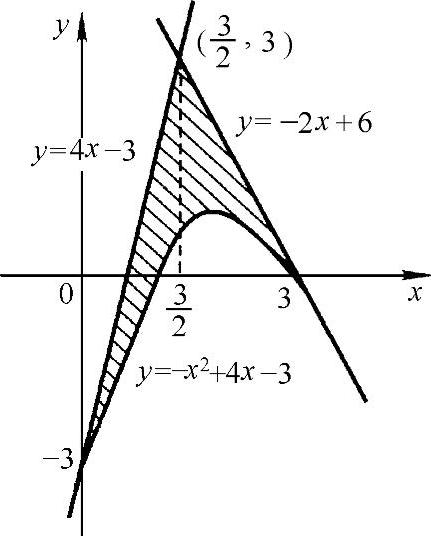
图 3-18

(https://www.xing528.com)

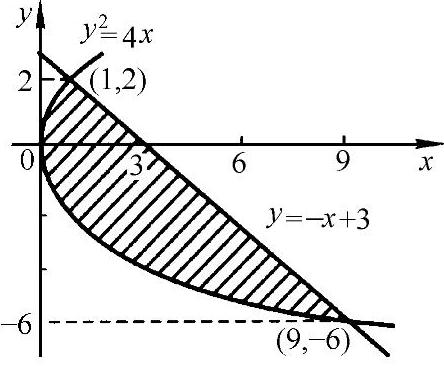
图 3-19

解 因为y²=4x，则2yy'=4，所以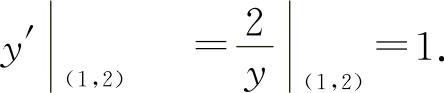

则法线方程为y-2=-（x-1），即y=-x+3.

解方程组求交点

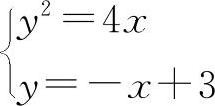得y²=-4y+12，解得y₁=-6，y₂=2.

则交点为（9，-6）与（1，2）.其平面图形如图3-19所示.

则面积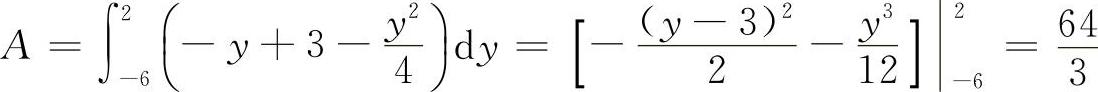

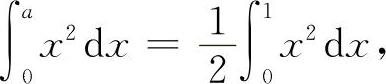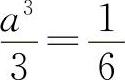4.由题意得 所以 ，得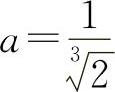

5.【分析】 应先求A₁+A₂，再求其具有极小值时的a的取值.

解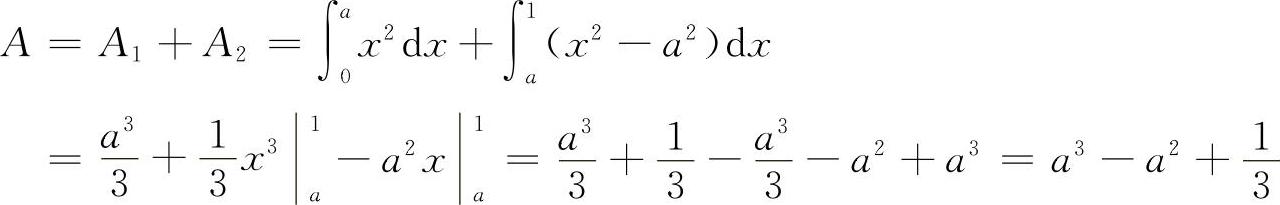

由于A=A₁+A₂是a的函数，对a求导得 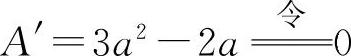，得a=0或，

A″=6a-2，由于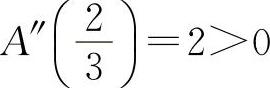所以当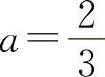时，A=A₁+A₂取得最小值.因此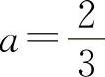为所求.

6.其平面图形如图3-20所示，则平面图形面积为

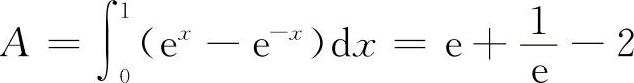
旋转体的体积为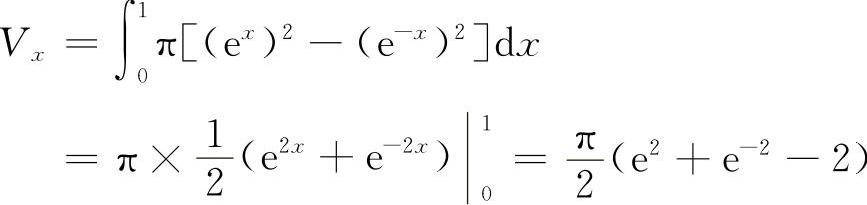

7.画出平面图形如图3-21所示.

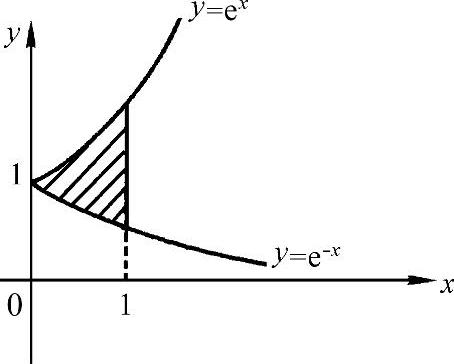
图 3-20

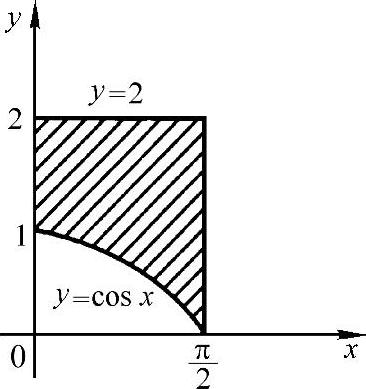
图 3-21

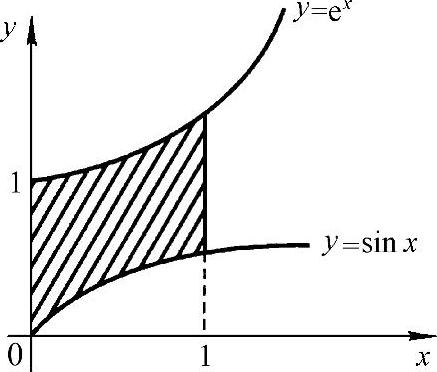
图 3-22

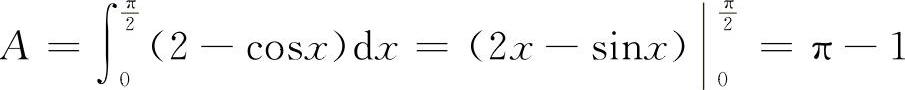
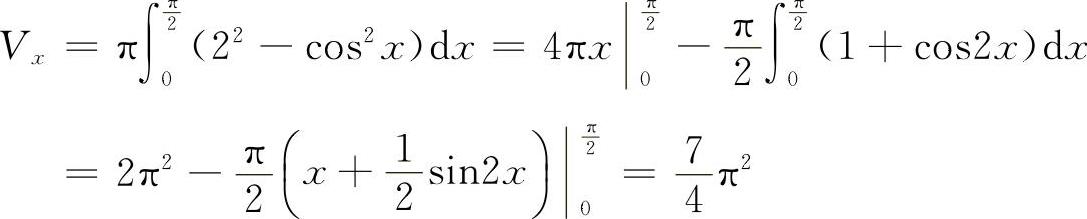
8.画出平面图形如图3-22所示，则有