高数练习题：曲线面积及切线法线所围图形

1.求下列曲线所围成的平面图形的面积.

（1）y=x²与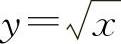 （2）y=x²，y=x，与y=2x

（3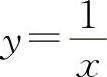），y=x，x=2

（4）y=x³与y=2x

2.求抛物线y=-x²+4x-3及其在点（0，-3）和点（3，0）处的切线所围成的平面图形的面积.

图 3-12

3.求抛物线y²=4x及其在点（1，2）处的法线所围成的平面图形的面积.

4.由曲线y=x²，x轴及x=1所围成的平面图形中，在0≤x≤1之间求一点A，过A点作x=a的直线将所围成的平面图形面积分成相等的两部分，求a值.

5.在曲线y=x²（0≤x≤1）上求一点（a，a²），过此点分别作平行于y轴和x轴的直线x=a和y=a²，则曲线y=x²与直线x=a和x轴围成的平面图形面积为A₁，曲线y=x²与直线y=a²和直线x=1围成的平面图形面积为A₂（如图3-13所示），试求a为何值时，A₁+A₂为最小.

6.求由曲线y=e^x，y=e^-x及x=1所围成的平面图形的面积以及此平面图形绕x轴旋转一周所成的旋转体的体积V_x.(www.xing528.com)

图 3-13

图 3-13

图 3-13

7.求由曲线y=cosx与直线y=2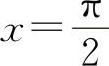，及y轴所围成的平面图形的面积以及此平面图形绕x轴旋转一周所成的旋转体的体积V_x.

8.求y=e^x，y=sinx，x=0与x=1所围成的平面图形绕x轴旋转一周所成的旋转体的体积V_x.

7.求由曲线y=cosx与直线y=2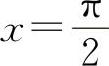，及y轴所围成的平面图形的面积以及此平面图形绕x轴旋转一周所成的旋转体的体积V_x.

8.求y=e^x，y=sinx，x=0与x=1所围成的平面图形绕x轴旋转一周所成的旋转体的体积V_x.

7.求由曲线y=cosx与直线y=2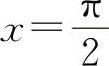，及y轴所围成的平面图形的面积以及此平面图形绕x轴旋转一周所成的旋转体的体积V_x.

8.求y=e^x，y=sinx，x=0与x=1所围成的平面图形绕x轴旋转一周所成的旋转体的体积V_x.