1.应选D选项 【分析】 根据原函数的定义来确定选项.
因为[2(e2x-e-2x)]'=4(e2x+e-2x)≠e2x-e-2x.所以选D选项.
2.应选A选项 【分析】 注意到常数的微分等于零,所以选项A不一定成立.
因为f(x)=g(x)+C时,仍有∫df(x)=∫d(g(x)+C)=∫dg(x).所以选A选项.
3.应选B选项 【分析】 根据积分公式∫f(x)dx=F(x)+C的结构式为
利用凑微分即可确定选项.因为
∫e-xf(e-x)dx=-∫f(e-x)de-x=-F(e-x)+C所以选B选项.
4.应选B选项 【分析】 由原函数的定义可知f(x)=(e-x)',即f(x)dx=de-x,因此∫xf(x)dx=∫xde-x=xe-x-∫e-xdx=xe-x+e-x+C=e-x(x+1)+C所以选B选项.
利用凑微分即可确定选项.因为
∫e-xf(e-x)dx=-∫f(e-x)de-x=-F(e-x)+C所以选B选项.
4.应选B选项 【分析】 由原函数的定义可知f(x)=(e-x)',即f(x)dx=de-x,因此∫xf(x)dx=∫xde-x=xe-x-∫e-xdx=xe-x+e-x+C=e-x(x+1)+C所以选B选项.(https://www.xing528.com)
5.应选B选项 【分析】 本题是函数概念、导数概念和不定积分概念的综合题,由于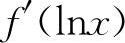
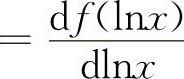 ,又∫f'(x)dx=f(x)+C,而∫f'(lnx)dx≠f(lnx)+C,利用上述概念及凑微分,则有
,又∫f'(x)dx=f(x)+C,而∫f'(lnx)dx≠f(lnx)+C,利用上述概念及凑微分,则有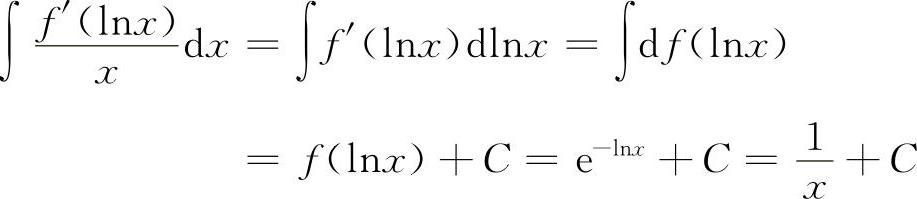 所以选B选项.
所以选B选项.
5.应选B选项 【分析】 本题是函数概念、导数概念和不定积分概念的综合题,由于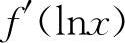
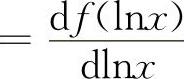 ,又∫f'(x)dx=f(x)+C,而∫f'(lnx)dx≠f(lnx)+C,利用上述概念及凑微分,则有
,又∫f'(x)dx=f(x)+C,而∫f'(lnx)dx≠f(lnx)+C,利用上述概念及凑微分,则有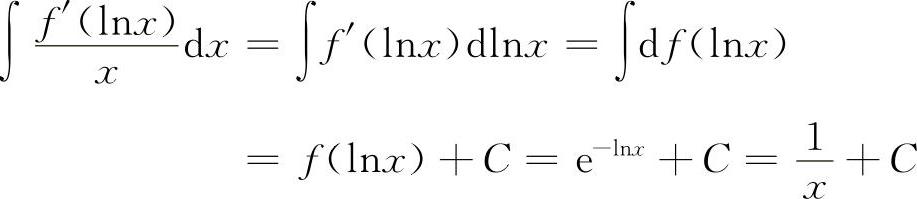 所以选B选项.
所以选B选项.
6.应选D选项 【分析】 利用凑微分和不定积分公式的结构式,即可.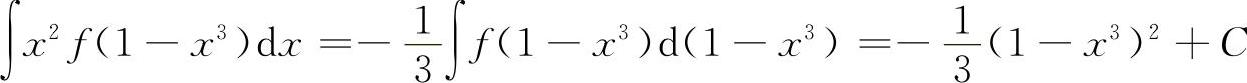 所以选D选项.
所以选D选项.
7.【分析】 利用凑微分积分.
6.应选D选项 【分析】 利用凑微分和不定积分公式的结构式,即可.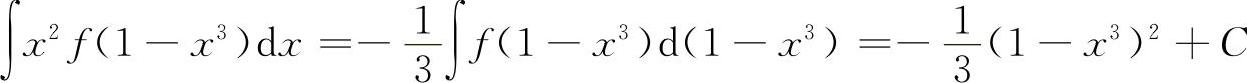 所以选D选项.
所以选D选项.
7.【分析】 利用凑微分积分.
8.【分析】 本大题主要是用分部积分法求解.
8.【分析】 本大题主要是用分部积分法求解.
解 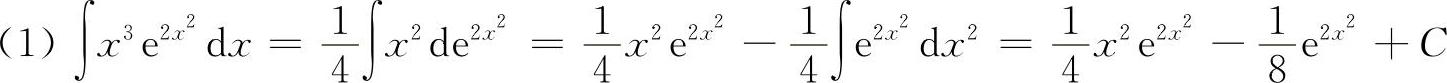
解 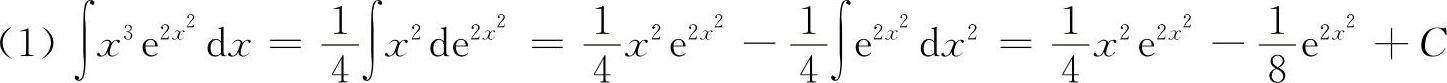
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




