1.利用四则运算法则求函数的导数或在某点的导数值.共考20次,此类型题为必考题.
(1)(0622)设函数y=x4sinx,求dy.
(2)(0705)设函数y=sin(x2-1),则dy=( ).
A.cos(x2-1)dx B.-cos(x2-1)dx
C.2xcos(x2-1)dx D.-2xcos(x2-1)dx
(3)(0822)设函数y=x3+sinx+3,求y'.
(4)(0902)设函数y=x2+sinx+ln2,则y'=( ).
A.2x+sinx B.2x+cosx
C.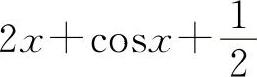 D.2x
D.2x
(5)(0903)设函数f(x)=exlnx,则f'(1)=().
A.0 B.1 C.e D.2e
C.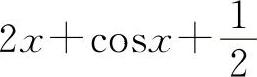 D.2x
D.2x
(5)(0903)设函数f(x)=exlnx,则f'(1)=().
A.0 B.1 C.e D.2e
C.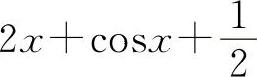 D.2x
D.2x
(5)(0903)设函数f(x)=exlnx,则f'(1)=().
A.0 B.1 C.e D.2e
(6)(1022)设函数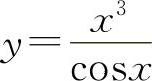 ,求dy.
,求dy.
(6)(1022)设函数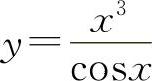 ,求dy.
,求dy.
(6)(1022)设函数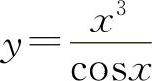 ,求dy.
,求dy.
(7)(1122)设函数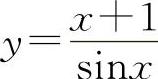 ,求y'.
,求y'.
(7)(1122)设函数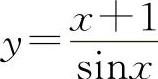 ,求y'.
,求y'.
(7)(1122)设函数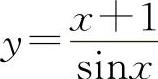 ,求y'.
,求y'.
(8)(1203)设函数f(x)=cosx,则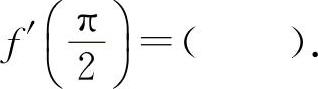
(8)(1203)设函数f(x)=cosx,则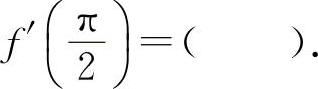
(8)(1203)设函数f(x)=cosx,则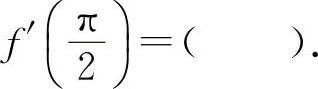
A.-1 B.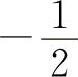
C.0 D.1
A.-1 B.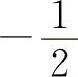
C.0 D.1
A.-1 B.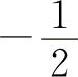
C.0 D.1
(9)(1302)设函数y=ex-ln3,则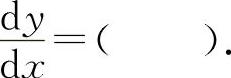
(9)(1302)设函数y=ex-ln3,则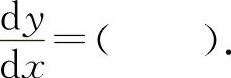
(9)(1302)设函数y=ex-ln3,则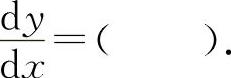
【分析】 这些试题都是利用基本初等函数的求导公式及导数的四则运算来计算的.这些题都是属于基本运算的试题,是每年专升本必考的内容之一.
(1)y'=4x3sinx+x4cosx,所以dy=(4x3sinx+x4cosx)dx.
(2)选C选项.因为y'=cos(x2-1)·2x,所以dy=2xcos(x2-1)dx.
(3)y'=(x3)'+(sinx)'+3'=3x2+cosx.
(4)选B选项.y'=2x+cosx.
【分析】 这些试题都是利用基本初等函数的求导公式及导数的四则运算来计算的.这些题都是属于基本运算的试题,是每年专升本必考的内容之一.
(1)y'=4x3sinx+x4cosx,所以dy=(4x3sinx+x4cosx)dx.
(2)选C选项.因为y'=cos(x2-1)·2x,所以dy=2xcos(x2-1)dx.
(3)y'=(x3)'+(sinx)'+3'=3x2+cosx.
(4)选B选项.y'=2x+cosx.
【分析】 这些试题都是利用基本初等函数的求导公式及导数的四则运算来计算的.这些题都是属于基本运算的试题,是每年专升本必考的内容之一.
(1)y'=4x3sinx+x4cosx,所以dy=(4x3sinx+x4cosx)dx.
(2)选C选项.因为y'=cos(x2-1)·2x,所以dy=2xcos(x2-1)dx.
(3)y'=(x3)'+(sinx)'+3'=3x2+cosx.
(4)选B选项.y'=2x+cosx.
(5)选C选项.因为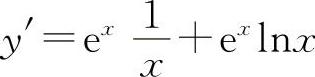 ,故
,故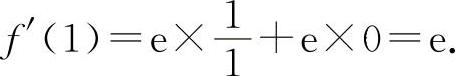
(5)选C选项.因为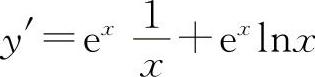 ,故
,故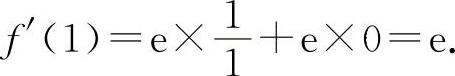
(5)选C选项.因为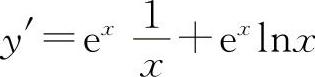 ,故
,故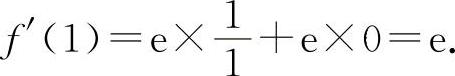
(6)因为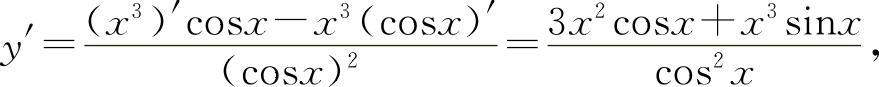 所以
所以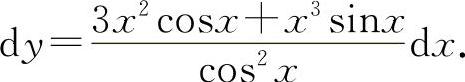
(6)因为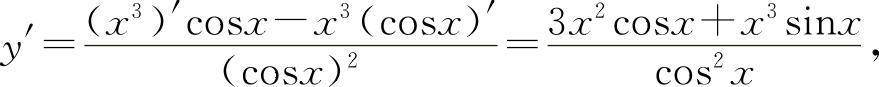 所以
所以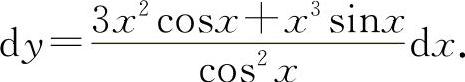
(6)因为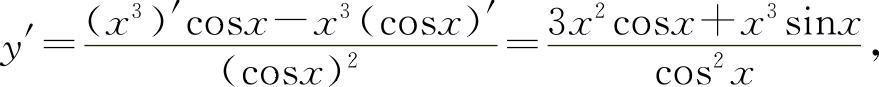 所以
所以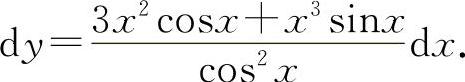
(8)选A选项.因为f'(x)=-sinx,所以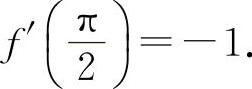
(9)选A选项.
2.复合函数的求导.共考18次,考到的概率为90%.
(1)(0602)设函数y=e2x+5,则y'=( ).
A.e2x B.2e2x C.2e2x+5 D.2ex+5
(8)选A选项.因为f'(x)=-sinx,所以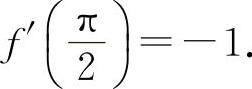
(9)选A选项.
2.复合函数的求导.共考18次,考到的概率为90%.
(1)(0602)设函数y=e2x+5,则y'=( ).
A.e2x B.2e2x C.2e2x+5 D.2ex+5
(8)选A选项.因为f'(x)=-sinx,所以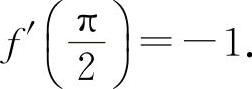
(9)选A选项.
2.复合函数的求导.共考18次,考到的概率为90%.
(1)(0602)设函数y=e2x+5,则y'=( ).
A.e2x B.2e2x C.2e2x+5 D.2ex+5
(2)(0722)设函数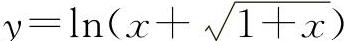 ,求y'.
,求y'.
(3)(0922)设函数y=esinx,求dy.
(4)(1003)设函数f(x)=cos2x,则f'(x)=( ).
A.2sin2x B.-2sin2x C.sin2x D.-sin2x
(5)(1222)设函数y=ln(x2+1),求dy.
(6)(1322)设函数y=sinx2+2x,求dy.
【分析】 复合函数求导是每年必考的试题之一,其计算的关键是分清复合的过程.另外,要注意:只有基本初等函数才能用公式,也即,导数公式的结构式为
(2)(0722)设函数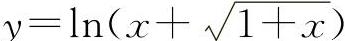 ,求y'.
,求y'.
(3)(0922)设函数y=esinx,求dy.
(4)(1003)设函数f(x)=cos2x,则f'(x)=( ).
A.2sin2x B.-2sin2x C.sin2x D.-sin2x
(5)(1222)设函数y=ln(x2+1),求dy.
(6)(1322)设函数y=sinx2+2x,求dy.
【分析】 复合函数求导是每年必考的试题之一,其计算的关键是分清复合的过程.另外,要注意:只有基本初等函数才能用公式,也即,导数公式的结构式为
(2)(0722)设函数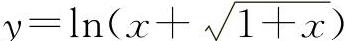 ,求y'.
,求y'.
(3)(0922)设函数y=esinx,求dy.
(4)(1003)设函数f(x)=cos2x,则f'(x)=( ).
A.2sin2x B.-2sin2x C.sin2x D.-sin2x
(5)(1222)设函数y=ln(x2+1),求dy.
(6)(1322)设函数y=sinx2+2x,求dy.
【分析】 复合函数求导是每年必考的试题之一,其计算的关键是分清复合的过程.另外,要注意:只有基本初等函数才能用公式,也即,导数公式的结构式为
y=sin▭,则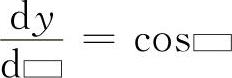
式中的“▭”可以是变量x,也可以是x的函数.
y=sin▭,则
式中的“▭”可以是变量x,也可以是x的函数.
y=sin▭,则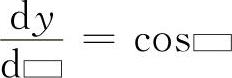
式中的“▭”可以是变量x,也可以是x的函数.
例如y=sinx2,则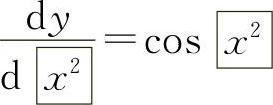 ,而
,而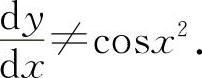 应该用复合函数求导公式.
应该用复合函数求导公式.
解 (1)选B选项.因为y'=2e2x.
例如y=sinx2,则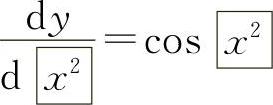 ,而
,而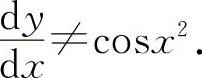 应该用复合函数求导公式.
应该用复合函数求导公式.
解 (1)选B选项.因为y'=2e2x.
例如y=sinx2,则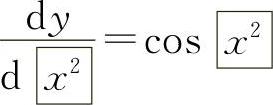 ,而
,而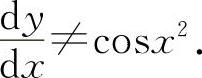 应该用复合函数求导公式.
应该用复合函数求导公式.
解 (1)选B选项.因为y'=2e2x.
(3)y'=esinxcosx,则dy=cosxesinxdx.
(4)选B选项.因为f'(x)=-sin2x·2=-2sin2x.
(3)y'=esinxcosx,则dy=cosxesinxdx.
(4)选B选项.因为f'(x)=-sin2x·2=-2sin2x.
(3)y'=esinxcosx,则dy=cosxesinxdx.
(4)选B选项.因为f'(x)=-sin2x·2=-2sin2x.
(5)因为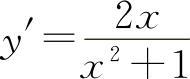 ,所以
,所以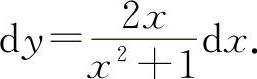
(5)因为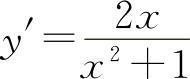 ,所以
,所以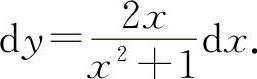
(5)因为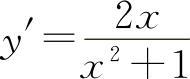 ,所以
,所以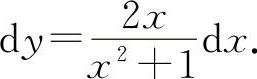
(6)因为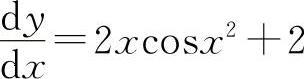 ,所以dy=(2xcosx2+2)dx.
,所以dy=(2xcosx2+2)dx.
3.隐函数求导.
注:此处试题合并到多元函数的隐函数求导.
4.二阶导数与高阶导数.共考19次,考到的概率为95%.
(1)(0311)设函数y=x2+e2x,则y的50阶导数y(50)=____.
(2)(0615)设函数y=sin2x,则y″=____.
(3)(0714)设函数y=e-x,则y‴=____.
(4)(0814)设函数y=x5,y″=____.
(5)(0915)设函数y=xsinx,则y″=____.
(6)(1015)设函数y=ln(1+x),则y″=____.
(7)(1114)设函数y=sinx,则y‴=____.
(8)(1215)设函数f(x)=cosx,则f″(x)=____.
(9)(1314)设函数y=ex+1,则y″=____.
【分析】 这类试题主要考查二阶导数和二阶导数值的求法,因此应先求y'再求y″.最后再将x0代入y″中即可.
函数的n阶段数是2003年大纲中新增加的内容,希望考生引起重视.这类题目的关键是由一阶、二阶、三阶等有限阶导数总结出一般的规律.
解(1)填250e2x.因为y'=2x+2e2x;y″=2+22e2x;y‴=23e2x;…;y(50)=250e2x.
(2)填-4sin2x.因为y'=2cos2x,y″=-4sin2x.
(3)填-e-x.因为y'=-e-x,y″=e-x,y‴=-e-x.
(4)填20x3.因为y'=5x4,y″=20x3.
(5)填2cosx-xsinx.因为y'=sinx+xcosx,y″=cosx+cosx-xsinx=2cosx-xsinx.
(6)因为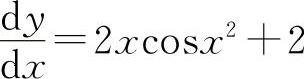 ,所以dy=(2xcosx2+2)dx.
,所以dy=(2xcosx2+2)dx.
3.隐函数求导.
注:此处试题合并到多元函数的隐函数求导.
4.二阶导数与高阶导数.共考19次,考到的概率为95%.
(1)(0311)设函数y=x2+e2x,则y的50阶导数y(50)=____.
(2)(0615)设函数y=sin2x,则y″=____.
(3)(0714)设函数y=e-x,则y‴=____.
(4)(0814)设函数y=x5,y″=____.
(5)(0915)设函数y=xsinx,则y″=____.
(6)(1015)设函数y=ln(1+x),则y″=____.
(7)(1114)设函数y=sinx,则y‴=____.
(8)(1215)设函数f(x)=cosx,则f″(x)=____.
(9)(1314)设函数y=ex+1,则y″=____.
【分析】 这类试题主要考查二阶导数和二阶导数值的求法,因此应先求y'再求y″.最后再将x0代入y″中即可.
函数的n阶段数是2003年大纲中新增加的内容,希望考生引起重视.这类题目的关键是由一阶、二阶、三阶等有限阶导数总结出一般的规律.
解(1)填250e2x.因为y'=2x+2e2x;y″=2+22e2x;y‴=23e2x;…;y(50)=250e2x.
(2)填-4sin2x.因为y'=2cos2x,y″=-4sin2x.
(3)填-e-x.因为y'=-e-x,y″=e-x,y‴=-e-x.
(4)填20x3.因为y'=5x4,y″=20x3.
(5)填2cosx-xsinx.因为y'=sinx+xcosx,y″=cosx+cosx-xsinx=2cosx-xsinx.
(6)因为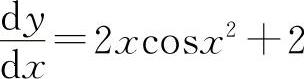 ,所以dy=(2xcosx2+2)dx.
,所以dy=(2xcosx2+2)dx.
3.隐函数求导.
注:此处试题合并到多元函数的隐函数求导.
4.二阶导数与高阶导数.共考19次,考到的概率为95%.
(1)(0311)设函数y=x2+e2x,则y的50阶导数y(50)=____.
(2)(0615)设函数y=sin2x,则y″=____.
(3)(0714)设函数y=e-x,则y‴=____.
(4)(0814)设函数y=x5,y″=____.
(5)(0915)设函数y=xsinx,则y″=____.
(6)(1015)设函数y=ln(1+x),则y″=____.
(7)(1114)设函数y=sinx,则y‴=____.
(8)(1215)设函数f(x)=cosx,则f″(x)=____.
(9)(1314)设函数y=ex+1,则y″=____.
【分析】 这类试题主要考查二阶导数和二阶导数值的求法,因此应先求y'再求y″.最后再将x0代入y″中即可.
函数的n阶段数是2003年大纲中新增加的内容,希望考生引起重视.这类题目的关键是由一阶、二阶、三阶等有限阶导数总结出一般的规律.
解(1)填250e2x.因为y'=2x+2e2x;y″=2+22e2x;y‴=23e2x;…;y(50)=250e2x.
(2)填-4sin2x.因为y'=2cos2x,y″=-4sin2x.
(3)填-e-x.因为y'=-e-x,y″=e-x,y‴=-e-x.
(4)填20x3.因为y'=5x4,y″=20x3.
(5)填2cosx-xsinx.因为y'=sinx+xcosx,y″=cosx+cosx-xsinx=2cosx-xsinx.
(6)填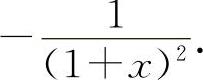 因为
因为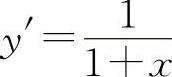 ,
,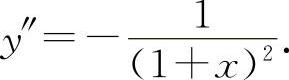
(7)填-cosx.因为y'=cosx,y″=-sinx,y‴=-cosx.
(8)填-cosx.因为f'(x)=-sinx,f″(x)=-cosx.
(9)填ex+1.
5.不定式极限的求法.共考12次,考到的概率为60%.
(6)填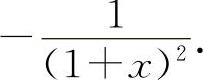 因为
因为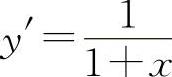 ,
,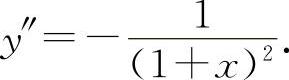
(7)填-cosx.因为y'=cosx,y″=-sinx,y‴=-cosx.
(8)填-cosx.因为f'(x)=-sinx,f″(x)=-cosx.
(9)填ex+1.
5.不定式极限的求法.共考12次,考到的概率为60%.
(6)填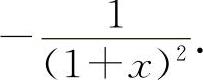 因为
因为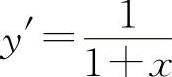 ,
,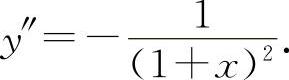
(7)填-cosx.因为y'=cosx,y″=-sinx,y‴=-cosx.
(8)填-cosx.因为f'(x)=-sinx,f″(x)=-cosx.
(9)填ex+1.
5.不定式极限的求法.共考12次,考到的概率为60%.
(1)(0721)求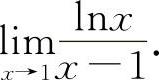
(1)(0721)求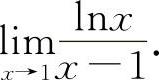
(1)(0721)求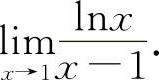
(2)(0801)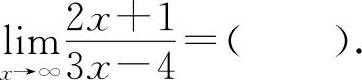
(2)(0801)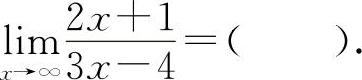
(2)(0801)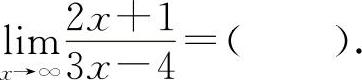
A.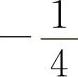 B.0 C.
B.0 C.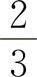 D.1
D.1
A. B.0 C.
B.0 C.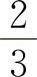 D.1
D.1
A.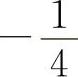 B.0 C.
B.0 C.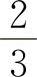 D.1
D.1
(3)(0911)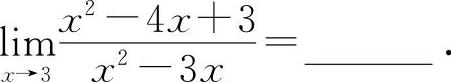
(3)(0911)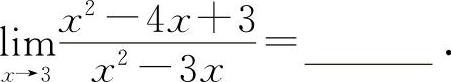
(3)(0911)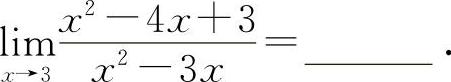
(4)(1221)求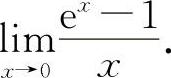
(4)(1221)求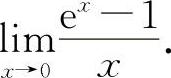
(4)(1221)求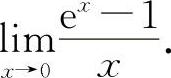
【分析】 对于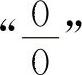 或
或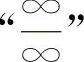 的不定式极限,通常可用洛必达法则计算.对于其他类型的不定式极限应先化为
的不定式极限,通常可用洛必达法则计算.对于其他类型的不定式极限应先化为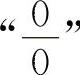 或
或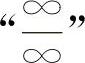 ,再用洛必达法则计算.
,再用洛必达法则计算.
注意:洛必达法则是求不定式极限的有效方法之一,但不是万能的.求极限的最佳方法是等价无穷小代换与洛必达法则的混合使用.
【分析】 对于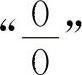 或
或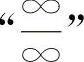 的不定式极限,通常可用洛必达法则计算.对于其他类型的不定式极限应先化为
的不定式极限,通常可用洛必达法则计算.对于其他类型的不定式极限应先化为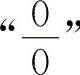 或
或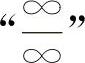 ,再用洛必达法则计算.
,再用洛必达法则计算.
注意:洛必达法则是求不定式极限的有效方法之一,但不是万能的.求极限的最佳方法是等价无穷小代换与洛必达法则的混合使用.
【分析】 对于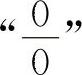 或
或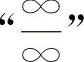 的不定式极限,通常可用洛必达法则计算.对于其他类型的不定式极限应先化为
的不定式极限,通常可用洛必达法则计算.对于其他类型的不定式极限应先化为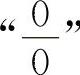 或
或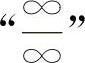 ,再用洛必达法则计算.
,再用洛必达法则计算.
注意:洛必达法则是求不定式极限的有效方法之一,但不是万能的.求极限的最佳方法是等价无穷小代换与洛必达法则的混合使用.
解 (1)
(2)选C选项.
解 (1)
(2)选C选项.
解 (1)
(2)选C选项.
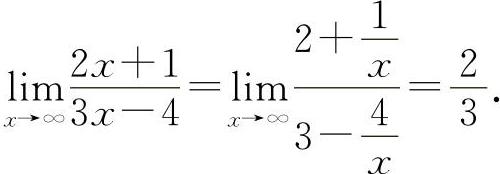 (3)填
(3)填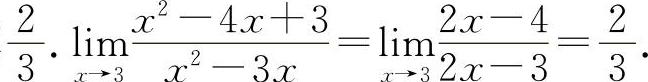
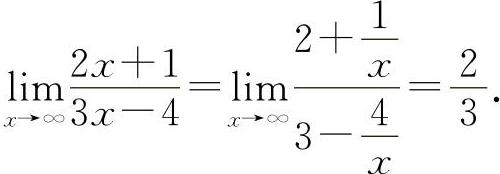 (3)填
(3)填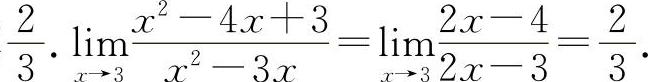
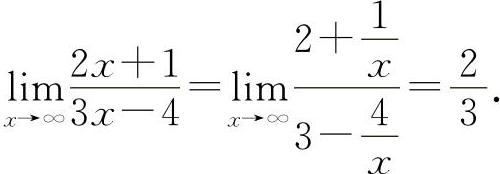 (3)填
(3)填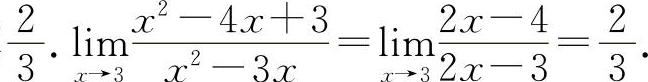
6.曲线在某点处的切线方程和法线方程.共考11次,考到的概率为55%.
(1)(0616)曲线y=x3-x在点(1,0)处的切线方程y=____.
(2)(0914)已知曲线y=ax3在x=1处的切线平行于直线y=2x-1,则a=____.
(3)(1016)设曲线y=axex在x=0处的切线斜率为2,则a=____.
(4)(1113)曲线y=2x2在点(1,2)处的切线方程y=____.
(5)(1216)曲线y=sin(x+1)在点(-1,0)处的切线斜率为____.
(6)(1316)设曲线y=ax2+2x在点(1,a+2)处的切线与直线y=4x平行,则a=____.
【分析】 利用函数在某点的导数是表示过该点的切线的斜率进行解题____.
解 (1)填2(x-1).因为y'=3x2-1,y'(1)=2,则切线方程为y=2(x-1)____.
6.曲线在某点处的切线方程和法线方程.共考11次,考到的概率为55%.
(1)(0616)曲线y=x3-x在点(1,0)处的切线方程y=____.
(2)(0914)已知曲线y=ax3在x=1处的切线平行于直线y=2x-1,则a=____.
(3)(1016)设曲线y=axex在x=0处的切线斜率为2,则a=____.
(4)(1113)曲线y=2x2在点(1,2)处的切线方程y=____.
(5)(1216)曲线y=sin(x+1)在点(-1,0)处的切线斜率为____.
(6)(1316)设曲线y=ax2+2x在点(1,a+2)处的切线与直线y=4x平行,则a=____.
【分析】 利用函数在某点的导数是表示过该点的切线的斜率进行解题____.
解 (1)填2(x-1).因为y'=3x2-1,y'(1)=2,则切线方程为y=2(x-1)____.
6.曲线在某点处的切线方程和法线方程.共考11次,考到的概率为55%.
(1)(0616)曲线y=x3-x在点(1,0)处的切线方程y=____.
(2)(0914)已知曲线y=ax3在x=1处的切线平行于直线y=2x-1,则a=____.
(3)(1016)设曲线y=axex在x=0处的切线斜率为2,则a=____.
(4)(1113)曲线y=2x2在点(1,2)处的切线方程y=____.
(5)(1216)曲线y=sin(x+1)在点(-1,0)处的切线斜率为____.
(6)(1316)设曲线y=ax2+2x在点(1,a+2)处的切线与直线y=4x平行,则a=____.
【分析】 利用函数在某点的导数是表示过该点的切线的斜率进行解题____.
解 (1)填2(x-1).因为y'=3x2-1,y'(1)=2,则切线方程为y=2(x-1)____.
(2)填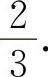 因为y'|x=1=3a=2.所以
因为y'|x=1=3a=2.所以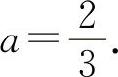
(3)填2.因为y'|x=0=a(x+1)ex|x=0=a=2.
(4)填4x-2.因为y'(1)=4x|x=1=4,所以y-2=4(x-1)即y=4x-2.
(5)填1.因为y'=cos(x+1),所以y'(-1)=1.
(6)填1.因为y'|x=1=2a+2=4,所以a=1.
7.函数特性的研究Ⅰ.共考24次,此类型题为必考题.
(1)(0614)函数y=ex2的极值点为x=____.
(2)(0704)设函数f(x)在x=0处连续,当x<0时,f'(x)<0;当x>0时,f'(x)>0,则( ).
A.f(0)是极小值 B.f(0)是极大值
C.f(0)不是极值 D.f(0)既是极大值又是极小值
(3)(0715)函数y=xlnx的单调增加区间是____.
(4)(0804)已知f(x)在区间(-∞,+∞)内为单调减函数,且f(x)>f(1),则x的取值范围是( ).
A.(-∞,-1) B.(-∞,1) C.(1,+∞) D.(-∞,+∞)
(2)填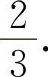 因为y'|x=1=3a=2.所以
因为y'|x=1=3a=2.所以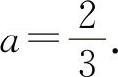
(3)填2.因为y'|x=0=a(x+1)ex|x=0=a=2.
(4)填4x-2.因为y'(1)=4x|x=1=4,所以y-2=4(x-1)即y=4x-2.
(5)填1.因为y'=cos(x+1),所以y'(-1)=1.
(6)填1.因为y'|x=1=2a+2=4,所以a=1.
7.函数特性的研究Ⅰ.共考24次,此类型题为必考题.
(1)(0614)函数y=ex2的极值点为x=____.
(2)(0704)设函数f(x)在x=0处连续,当x<0时,f'(x)<0;当x>0时,f'(x)>0,则( ).
A.f(0)是极小值 B.f(0)是极大值
C.f(0)不是极值 D.f(0)既是极大值又是极小值
(3)(0715)函数y=xlnx的单调增加区间是____.
(4)(0804)已知f(x)在区间(-∞,+∞)内为单调减函数,且f(x)>f(1),则x的取值范围是( ).
A.(-∞,-1) B.(-∞,1) C.(1,+∞) D.(-∞,+∞)
(2)填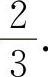 因为y'|x=1=3a=2.所以
因为y'|x=1=3a=2.所以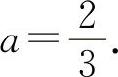
(3)填2.因为y'|x=0=a(x+1)ex|x=0=a=2.
(4)填4x-2.因为y'(1)=4x|x=1=4,所以y-2=4(x-1)即y=4x-2.
(5)填1.因为y'=cos(x+1),所以y'(-1)=1.
(6)填1.因为y'|x=1=2a+2=4,所以a=1.
7.函数特性的研究Ⅰ.共考24次,此类型题为必考题.
(1)(0614)函数y=ex2的极值点为x=____.
(2)(0704)设函数f(x)在x=0处连续,当x<0时,f'(x)<0;当x>0时,f'(x)>0,则( ).
A.f(0)是极小值 B.f(0)是极大值
C.f(0)不是极值 D.f(0)既是极大值又是极小值
(3)(0715)函数y=xlnx的单调增加区间是____.
(4)(0804)已知f(x)在区间(-∞,+∞)内为单调减函数,且f(x)>f(1),则x的取值范围是( ).
A.(-∞,-1) B.(-∞,1) C.(1,+∞) D.(-∞,+∞)
(5)(0815)曲线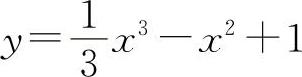 的拐点坐标(x0,y0)=____.
的拐点坐标(x0,y0)=____.
(6)(0916)曲线y=x5-10x2+8的拐点坐标(x0,y0)=____.
(7)(1004)下列函数在区间(0,+∞)内单调减少的是( ).
(5)(0815)曲线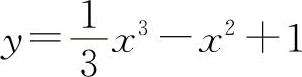 的拐点坐标(x0,y0)=____.
的拐点坐标(x0,y0)=____.
(6)(0916)曲线y=x5-10x2+8的拐点坐标(x0,y0)=____.
(7)(1004)下列函数在区间(0,+∞)内单调减少的是( ).
(5)(0815)曲线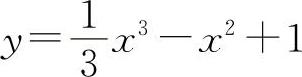 的拐点坐标(x0,y0)=____.
的拐点坐标(x0,y0)=____.
(6)(0916)曲线y=x5-10x2+8的拐点坐标(x0,y0)=____.
(7)(1004)下列函数在区间(0,+∞)内单调减少的是( ).
A.y=x B.y=ex C.y=lnx D.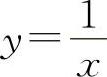
(8)(1014)曲线y=x3+3x2+1的拐点坐标为____.
(9)(1104)已知函数y(x)在区间(-∞,+∞)内单调增加,则使f(x)>f(2)成立的x的取值范围是( ).
A.(2,+∞) B.(-∞,0) C.(-∞,2) D.(0,2)
A.y=x B.y=ex C.y=lnx D.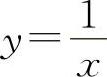
(8)(1014)曲线y=x3+3x2+1的拐点坐标为____.
(9)(1104)已知函数y(x)在区间(-∞,+∞)内单调增加,则使f(x)>f(2)成立的x的取值范围是( ).
A.(2,+∞) B.(-∞,0) C.(-∞,2) D.(0,2)
A.y=x B.y=ex C.y=lnx D.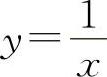
(8)(1014)曲线y=x3+3x2+1的拐点坐标为____.
(9)(1104)已知函数y(x)在区间(-∞,+∞)内单调增加,则使f(x)>f(2)成立的x的取值范围是( ).
A.(2,+∞) B.(-∞,0) C.(-∞,2) D.(0,2)
(10)(1115)函数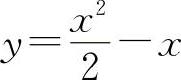 的单调增加区间是____.
的单调增加区间是____.
(11)(1204)下列区间为函数f(x)=sinx的单调增加区间的是( )
(10)(1115)函数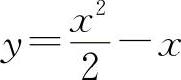 的单调增加区间是____.
的单调增加区间是____.
(11)(1204)下列区间为函数f(x)=sinx的单调增加区间的是( )
(10)(1115)函数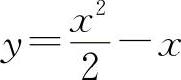 的单调增加区间是____.
的单调增加区间是____.
(11)(1204)下列区间为函数f(x)=sinx的单调增加区间的是( )
(12)(1214)曲线y=x3+3x的拐点坐标为____.
(13)(1313)曲线y=x3-3x2+5x-4的拐点坐标为____.
【分析】 选择题或填空题主要是考查对基本概念的掌握和理解.利用y'的符号来判定y的单调区间,利用y″的符号来判定曲线的凹凸区间以及拐点的求法.因此有下列答案.
(12)(1214)曲线y=x3+3x的拐点坐标为____.
(13)(1313)曲线y=x3-3x2+5x-4的拐点坐标为____.
【分析】 选择题或填空题主要是考查对基本概念的掌握和理解.利用y'的符号来判定y的单调区间,利用y″的符号来判定曲线的凹凸区间以及拐点的求法.因此有下列答案.
(12)(1214)曲线y=x3+3x的拐点坐标为____.
(13)(1313)曲线y=x3-3x2+5x-4的拐点坐标为____.
【分析】 选择题或填空题主要是考查对基本概念的掌握和理解.利用y'的符号来判定y的单调区间,利用y″的符号来判定曲线的凹凸区间以及拐点的求法.因此有下列答案.
解 (1)填0.因为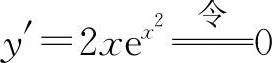 得x=0,且在x=0两侧的y'异号,所以x=0是极值点.
得x=0,且在x=0两侧的y'异号,所以x=0是极值点.
(2)选A选项.根据极值的第一充分条件可知A选项正确.
(3)填(e-1,+∞).因为y'=lnx+1,令y'>0,得x>e-1.
(4)选B选项.根据条件画出函数图像即可知B选项正确.
解 (1)填0.因为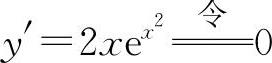 得x=0,且在x=0两侧的y'异号,所以x=0是极值点.
得x=0,且在x=0两侧的y'异号,所以x=0是极值点.
(2)选A选项.根据极值的第一充分条件可知A选项正确.
(3)填(e-1,+∞).因为y'=lnx+1,令y'>0,得x>e-1.
(4)选B选项.根据条件画出函数图像即可知B选项正确.
解 (1)填0.因为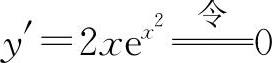 得x=0,且在x=0两侧的y'异号,所以x=0是极值点.(https://www.xing528.com)
得x=0,且在x=0两侧的y'异号,所以x=0是极值点.(https://www.xing528.com)
(2)选A选项.根据极值的第一充分条件可知A选项正确.
(3)填(e-1,+∞).因为y'=lnx+1,令y'>0,得x>e-1.
(4)选B选项.根据条件画出函数图像即可知B选项正确.
(5)填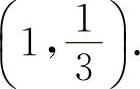 因为
因为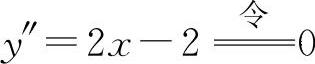 得x=1.因为在x=1两侧的y″异号,且当x=1时,
得x=1.因为在x=1两侧的y″异号,且当x=1时,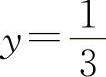 ,所以点
,所以点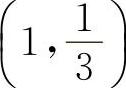 为拐点.
为拐点.
(6)填(1,-1).解法同(16)题.
(5)填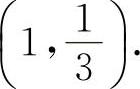 因为
因为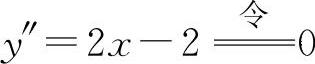 得x=1.因为在x=1两侧的y″异号,且当x=1时,
得x=1.因为在x=1两侧的y″异号,且当x=1时,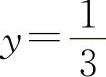 ,所以点
,所以点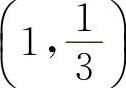 为拐点.
为拐点.
(6)填(1,-1).解法同(16)题.
(5)填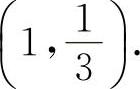 因为
因为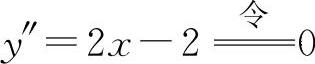 得x=1.因为在x=1两侧的y″异号,且当x=1时,
得x=1.因为在x=1两侧的y″异号,且当x=1时,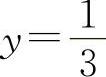 ,所以点
,所以点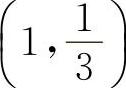 为拐点.
为拐点.
(6)填(1,-1).解法同(16)题.
(7)选D选项.因为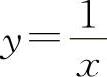 的
的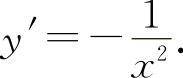
(8)填(-1,3).因为由y″=6x+6=0得x=-1,y=3,且在x=-1两侧y″异号,故拐点坐标为(-1,3).
(9)选A选项.根据单调增加的定义可知A选项正确.
(10)填(1,+∞).因为y'=x-1>0时,x>1.
(11)选A选项.
(7)选D选项.因为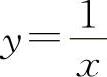 的
的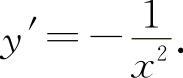
(8)填(-1,3).因为由y″=6x+6=0得x=-1,y=3,且在x=-1两侧y″异号,故拐点坐标为(-1,3).
(9)选A选项.根据单调增加的定义可知A选项正确.
(10)填(1,+∞).因为y'=x-1>0时,x>1.
(11)选A选项.
(7)选D选项.因为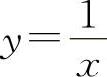 的
的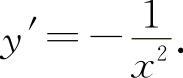
(8)填(-1,3).因为由y″=6x+6=0得x=-1,y=3,且在x=-1两侧y″异号,故拐点坐标为(-1,3).
(9)选A选项.根据单调增加的定义可知A选项正确.
(10)填(1,+∞).因为y'=x-1>0时,x>1.
(11)选A选项.
(12)填(0,0).因为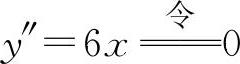 得x=0,则y(0)=0.
得x=0,则y(0)=0.
(12)填(0,0).因为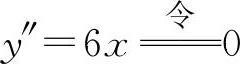 得x=0,则y(0)=0.
得x=0,则y(0)=0.
(12)填(0,0).因为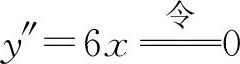 得x=0,则y(0)=0.
得x=0,则y(0)=0.
(13)填(1,-1).因为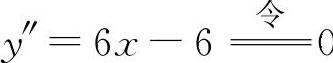 ,得x=1,此时y(1)=-1,所以拐点坐标为(1,-1).
,得x=1,此时y(1)=-1,所以拐点坐标为(1,-1).
8.函数特性的研究Ⅱ.共考12次,考到的概率为60%.
(1)(0626)求函数f(x)=x3-3x+1的单调区间和极值.
(2)(0828)设函数f(x)=ax3+bx2+x在x=1处取得极大值5.
①求常数a和b.
②求函数f(x)的极小值.
(13)填(1,-1).因为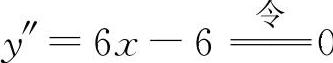 ,得x=1,此时y(1)=-1,所以拐点坐标为(1,-1).
,得x=1,此时y(1)=-1,所以拐点坐标为(1,-1).
8.函数特性的研究Ⅱ.共考12次,考到的概率为60%.
(1)(0626)求函数f(x)=x3-3x+1的单调区间和极值.
(2)(0828)设函数f(x)=ax3+bx2+x在x=1处取得极大值5.
①求常数a和b.
②求函数f(x)的极小值.
(13)填(1,-1).因为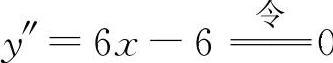 ,得x=1,此时y(1)=-1,所以拐点坐标为(1,-1).
,得x=1,此时y(1)=-1,所以拐点坐标为(1,-1).
8.函数特性的研究Ⅱ.共考12次,考到的概率为60%.
(1)(0626)求函数f(x)=x3-3x+1的单调区间和极值.
(2)(0828)设函数f(x)=ax3+bx2+x在x=1处取得极大值5.
①求常数a和b.
②求函数f(x)的极小值.
(3)(0926)求函数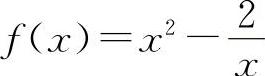 的单调区间、极值、凹凸区间和拐点.
的单调区间、极值、凹凸区间和拐点.
(3)(0926)求函数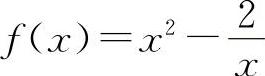 的单调区间、极值、凹凸区间和拐点.
的单调区间、极值、凹凸区间和拐点.
(3)(0926)求函数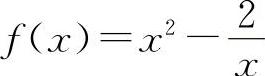 的单调区间、极值、凹凸区间和拐点.
的单调区间、极值、凹凸区间和拐点.
(4)(1126)求函数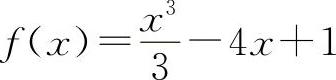 的单调区间、极值和曲线y=f(x)的凹凸区间.
的单调区间、极值和曲线y=f(x)的凹凸区间.
(5)(1226)求函数f(x)=x3-3x-2的单调区间和极值.
(6)(1326)求函数f(x)=x3-3x2-9x+2的单调区间和极值.
【分析】 这是导数应用的综合题.解题的关键是正确求出y'和y″,然后列表进行解答.
解 (1)函数的定义域为(-∞,+∞).
f'(x)=3x2-3.
令 f'(x)=0,得驻点x1=-1,x2=1.列表见表2-5.
表 2-5
(4)(1126)求函数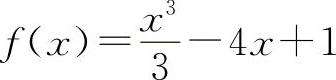 的单调区间、极值和曲线y=f(x)的凹凸区间.
的单调区间、极值和曲线y=f(x)的凹凸区间.
(5)(1226)求函数f(x)=x3-3x-2的单调区间和极值.
(6)(1326)求函数f(x)=x3-3x2-9x+2的单调区间和极值.
【分析】 这是导数应用的综合题.解题的关键是正确求出y'和y″,然后列表进行解答.
解 (1)函数的定义域为(-∞,+∞).
f'(x)=3x2-3.
令 f'(x)=0,得驻点x1=-1,x2=1.列表见表2-5.
表 2-5
(4)(1126)求函数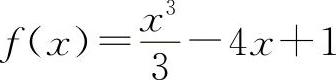 的单调区间、极值和曲线y=f(x)的凹凸区间.
的单调区间、极值和曲线y=f(x)的凹凸区间.
(5)(1226)求函数f(x)=x3-3x-2的单调区间和极值.
(6)(1326)求函数f(x)=x3-3x2-9x+2的单调区间和极值.
【分析】 这是导数应用的综合题.解题的关键是正确求出y'和y″,然后列表进行解答.
解 (1)函数的定义域为(-∞,+∞).
f'(x)=3x2-3.
令 f'(x)=0,得驻点x1=-1,x2=1.列表见表2-5.
表 2-5
函数f(x)的单调增区间为(-∞,-1],[1,+∞),单调减区间为[-1,1].
f(-1)=3为极大值,f(1)=-1为极小值.
(2)①f'(x)=3ax2+2bx+1
函数f(x)的单调增区间为(-∞,-1],[1,+∞),单调减区间为[-1,1].
f(-1)=3为极大值,f(1)=-1为极小值.
(2)①f'(x)=3ax2+2bx+1
函数f(x)的单调增区间为(-∞,-1],[1,+∞),单调减区间为[-1,1].
f(-1)=3为极大值,f(1)=-1为极小值.
(2)①f'(x)=3ax2+2bx+1
根据题意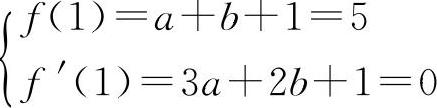
解得a=-9,b=13.
②令f'(x)=0,即27x2-26x-1=0.
根据题意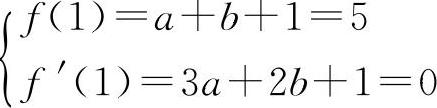
解得a=-9,b=13.
②令f'(x)=0,即27x2-26x-1=0.
根据题意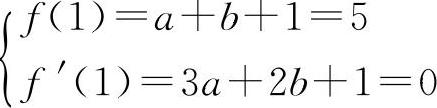
解得a=-9,b=13.
②令f'(x)=0,即27x2-26x-1=0.
解得 x1=1,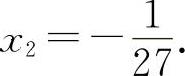
因为f″(x)=-54x+26,
解得 x1=1,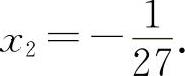
因为f″(x)=-54x+26,
解得 x1=1,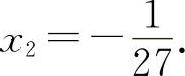
因为f″(x)=-54x+26,
且 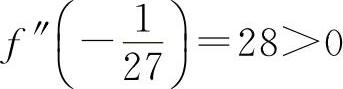 ,
,
且 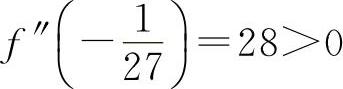 ,
,
且 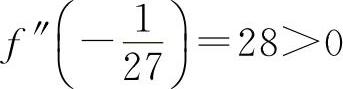 ,
,
所以 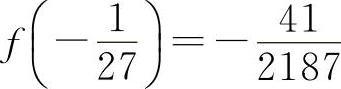 为极小值.
为极小值.
(3)f(x)的定义域(-∞,0)∪(0,+∞).
所以 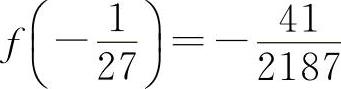 为极小值.
为极小值.
(3)f(x)的定义域(-∞,0)∪(0,+∞).
所以 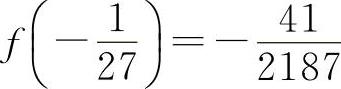 为极小值.
为极小值.
(3)f(x)的定义域(-∞,0)∪(0,+∞).
令f'(x)=0,得x=-1;令f″(x)=0,得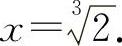 列表见表2-6.
列表见表2-6.
表 2-6
令f'(x)=0,得x=-1;令f″(x)=0,得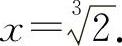 列表见表2-6.
列表见表2-6.
表 2-6
令f'(x)=0,得x=-1;令f″(x)=0,得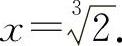 列表见表2-6.
列表见表2-6.
表 2-6
函数f(x)的单调减少区间为(-∞,-1);单调增加区间为(-1,0)∪(0,+∞),f(-1)=3为极小值.
函数f(x)的单调减少区间为(-∞,-1);单调增加区间为(-1,0)∪(0,+∞),f(-1)=3为极小值.
函数f(x)的单调减少区间为(-∞,-1);单调增加区间为(-1,0)∪(0,+∞),f(-1)=3为极小值.
函数f(x)的凹区间为 ),凸区间为(0,32),拐点坐标为
),凸区间为(0,32),拐点坐标为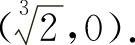
函数f(x)的凹区间为 ),凸区间为(0,32),拐点坐标为
),凸区间为(0,32),拐点坐标为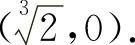
函数f(x)的凹区间为 ),凸区间为(0,32),拐点坐标为
),凸区间为(0,32),拐点坐标为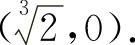
(4)函数的定义域为(-∞,+∞).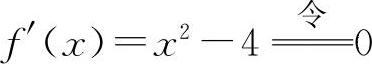 ,得x=±2.
,得x=±2.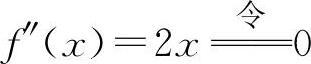 ,得x=0.
,得x=0.
列表如表2-7所示.
表 2-7
(4)函数的定义域为(-∞,+∞).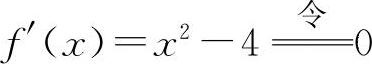 ,得x=±2.
,得x=±2.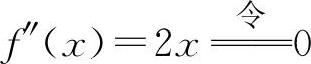 ,得x=0.
,得x=0.
列表如表2-7所示.
表 2-7
(4)函数的定义域为(-∞,+∞).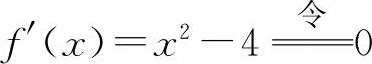 ,得x=±2.
,得x=±2.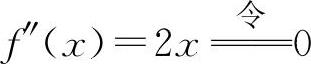 ,得x=0.
,得x=0.
列表如表2-7所示.
表 2-7
函数f(x)的单调增加区间为(-∞,-2)∪(2,+∞);单调减少区间为(-2,2);极大值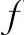
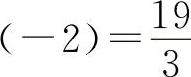 ,极小值
,极小值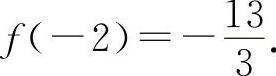
曲线y=f(x)的凹区间为(0,+∞),凸区间为(-∞,0).
函数f(x)的单调增加区间为(-∞,-2)∪(2,+∞);单调减少区间为(-2,2);极大值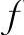
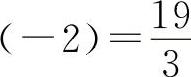 ,极小值
,极小值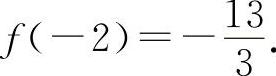
曲线y=f(x)的凹区间为(0,+∞),凸区间为(-∞,0).
函数f(x)的单调增加区间为(-∞,-2)∪(2,+∞);单调减少区间为(-2,2);极大值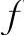
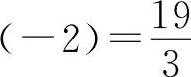 ,极小值
,极小值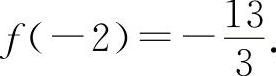
曲线y=f(x)的凹区间为(0,+∞),凸区间为(-∞,0).
(5)函数的定义域为(-∞,+∞).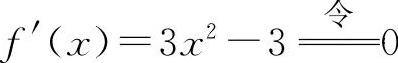 得x=±1.
得x=±1.
列表见表2-8.
表 2-8
(5)函数的定义域为(-∞,+∞).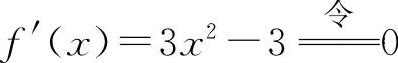 得x=±1.
得x=±1.
列表见表2-8.
表 2-8
(5)函数的定义域为(-∞,+∞).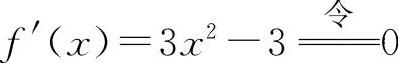 得x=±1.
得x=±1.
列表见表2-8.
表 2-8
函数f(x)的单调增区间为(-∞,-1),(1,+∞).
单调减区间为(-1,1).
函数f(x)的单调增区间为(-∞,-1),(1,+∞).
极大值为f(-1)=0,极小值为f(1)=-4.
单调减区间为(-1,1).
极大值为f(-1)=0,极小值为f(1)=-4.
函数f(x)的单调增区间为(-∞,-1),(1,+∞).
单调减区间为(-1,1).
极大值为f(-1)=0,极小值为f(1)=-4.
(6)f(x)的定义域为(-∞,+∞).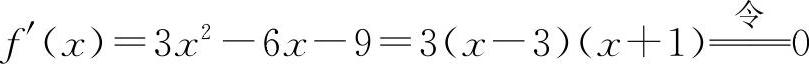 ,得x1=-1,x2=3.
,得x1=-1,x2=3.
列表见表2-9.
表 2-9
(6)f(x)的定义域为(-∞,+∞).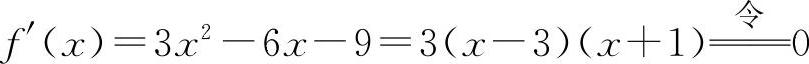 ,得x1=-1,x2=3.
,得x1=-1,x2=3.
列表见表2-9.
表 2-9
(6)f(x)的定义域为(-∞,+∞).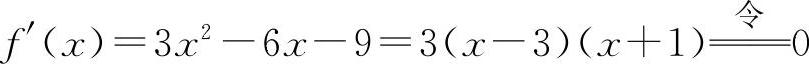 ,得x1=-1,x2=3.
,得x1=-1,x2=3.
列表见表2-9.
表 2-9
函数f(x)的单调增加区间为(-∞,-1),(3,+∞).
单调减少区间为(-1,3).
极小值为f(3)=-25;极大值f(-1)=7.
9.证明不等式.共考3次,考到的概率为15%.
函数f(x)的单调增加区间为(-∞,-1),(3,+∞).
单调减少区间为(-1,3).
极小值为f(3)=-25;极大值f(-1)=7.
9.证明不等式.共考3次,考到的概率为15%.
函数f(x)的单调增加区间为(-∞,-1),(3,+∞).
单调减少区间为(-1,3).
极小值为f(3)=-25;极大值f(-1)=7.
9.证明不等式.共考3次,考到的概率为15%.
(1)(0026)证明: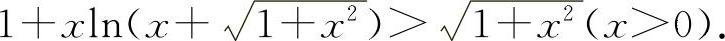
(1)(0026)证明: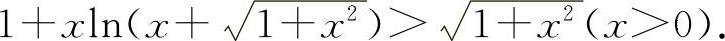
(1)(0026)证明: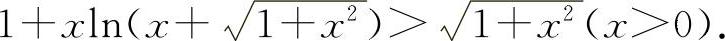
(2)(0328)证明:当x>0时,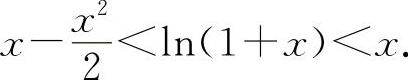
(3)(1027)证明:当x>1时,x>1+lnx.
【分析】 利用函数的单调性是证明不等式的一种常用的有效方法.其关键是构造一个函数,使其在某区间上是单调上升或单调下降.
(2)(0328)证明:当x>0时,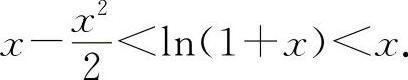
(3)(1027)证明:当x>1时,x>1+lnx.
【分析】 利用函数的单调性是证明不等式的一种常用的有效方法.其关键是构造一个函数,使其在某区间上是单调上升或单调下降.
(2)(0328)证明:当x>0时,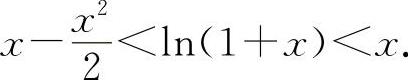
(3)(1027)证明:当x>1时,x>1+lnx.
【分析】 利用函数的单调性是证明不等式的一种常用的有效方法.其关键是构造一个函数,使其在某区间上是单调上升或单调下降.
解 (1)设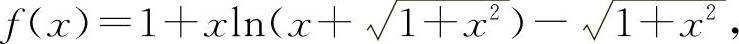
解 (1)设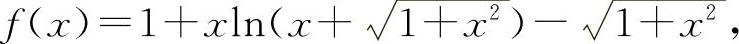
解 (1)设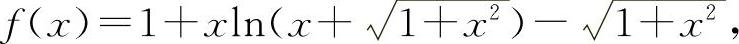
当x>0时f'(x)>0,则f(x)单调上升.
所以当x>0时,f(x)>f(0)=0,
当x>0时f'(x)>0,则f(x)单调上升.
所以当x>0时,f(x)>f(0)=0,
当x>0时f'(x)>0,则f(x)单调上升.
所以当x>0时,f(x)>f(0)=0,
即 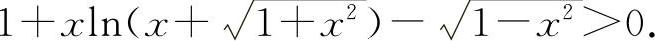
即 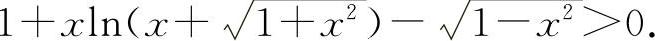
即 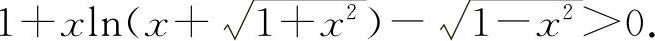
即得 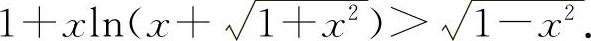
(2)这是两边不等式,因此应分别证明之.
即得 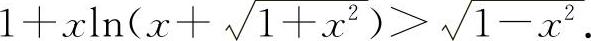
(2)这是两边不等式,因此应分别证明之.
即得 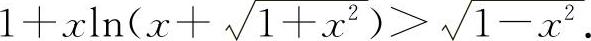
(2)这是两边不等式,因此应分别证明之.
设 f(x)=x-ln(1+x),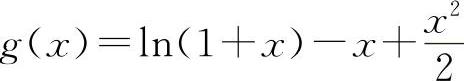 ,
,
设 f(x)=x-ln(1+x),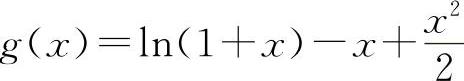 ,
,
设 f(x)=x-ln(1+x),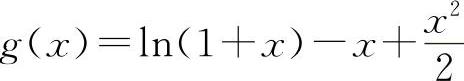 ,
,
当x>0时,f'(x)>0,g'(x)>0,则当x>0时,f(x)与g(x)均单调增加.
当x>0时,f'(x)>0,g'(x)>0,则当x>0时,f(x)与g(x)均单调增加.
当x>0时,f'(x)>0,g'(x)>0,则当x>0时,f(x)与g(x)均单调增加.
由于f(0)=0,g(0)=0,所以当x>0时,f(x)>f(0)=0,g(x)>g(0)=0即x-ln(1+x)>0;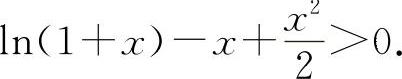
由于f(0)=0,g(0)=0,所以当x>0时,f(x)>f(0)=0,g(x)>g(0)=0即x-ln(1+x)>0;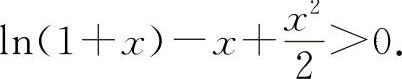
由于f(0)=0,g(0)=0,所以当x>0时,f(x)>f(0)=0,g(x)>g(0)=0即x-ln(1+x)>0;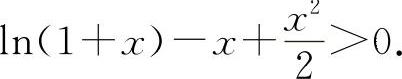
所以 x>ln(1+x),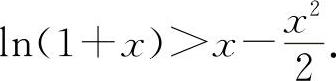
所以 x>ln(1+x),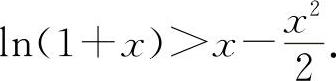
所以 x>ln(1+x),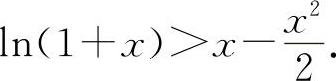
则有 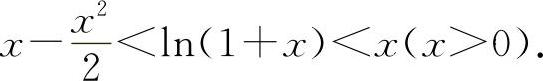
(3)证.设f(x)=x-1-lnx,
则有 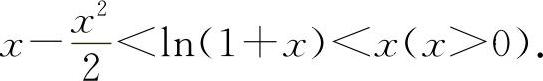
(3)证.设f(x)=x-1-lnx,
则有 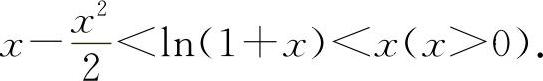
(3)证.设f(x)=x-1-lnx,
当x>1时,f'(x)>0,则f(x)单调上升,
所以当x>1时f(x)>f(1)=0.
即 x-1-lnx>0.
得 x>1+lnx.
10.应用题.共考5次,考到的概率为25%.
(1)(0726)上半部为等边三角形,下半部为矩形的窗户(如图2-7所示),其周长为12m.为使窗户的面积A达到最大,矩形的宽l应为多少米?
当x>1时,f'(x)>0,则f(x)单调上升,
所以当x>1时f(x)>f(1)=0.
即 x-1-lnx>0.
得 x>1+lnx.
10.应用题.共考5次,考到的概率为25%.
(1)(0726)上半部为等边三角形,下半部为矩形的窗户(如图2-7所示),其周长为12m.为使窗户的面积A达到最大,矩形的宽l应为多少米?
当x>1时,f'(x)>0,则f(x)单调上升,
所以当x>1时f(x)>f(1)=0.
即 x-1-lnx>0.
得 x>1+lnx.
10.应用题.共考5次,考到的概率为25%.
(1)(0726)上半部为等边三角形,下半部为矩形的窗户(如图2-7所示),其周长为12m.为使窗户的面积A达到最大,矩形的宽l应为多少米?
图 2-7
(2)(0826)设抛物线y=1-x2与x轴的交点为A,B,在它们所围成的平面区域内,以线段AB为下底作内接等腰梯形ABCD(如图2-8所示).设梯形上底CD长为2x,面积为S(x).
①写出S(x)的表达式.
②求S(x)的最大值.
图 2-7
(2)(0826)设抛物线y=1-x2与x轴的交点为A,B,在它们所围成的平面区域内,以线段AB为下底作内接等腰梯形ABCD(如图2-8所示).设梯形上底CD长为2x,面积为S(x).
①写出S(x)的表达式.
②求S(x)的最大值.
图 2-7
(2)(0826)设抛物线y=1-x2与x轴的交点为A,B,在它们所围成的平面区域内,以线段AB为下底作内接等腰梯形ABCD(如图2-8所示).设梯形上底CD长为2x,面积为S(x).
①写出S(x)的表达式.
②求S(x)的最大值.
图 2-8
(3)(1026)在半径为R的半圆内作一内接矩形,其中的一边在直径上,另外两个顶点在圆周上(如图2-9所示).当矩形的长和宽各为多少时矩形面积最大?最大值是多少?
图 2-8
(3)(1026)在半径为R的半圆内作一内接矩形,其中的一边在直径上,另外两个顶点在圆周上(如图2-9所示).当矩形的长和宽各为多少时矩形面积最大?最大值是多少?
图 2-8
(3)(1026)在半径为R的半圆内作一内接矩形,其中的一边在直径上,另外两个顶点在圆周上(如图2-9所示).当矩形的长和宽各为多少时矩形面积最大?最大值是多少?
图 2-9
(4)(1127)在抛物线y=1-x2与x轴所围成的平面区域内,做一内接矩形ABCD,其一边AB在x轴上(如图2-10所示).设AB长为2x,矩形面积为S(x).
①写出S(x)的表达式.
②求S(x)的最大值.
图 2-9
(4)(1127)在抛物线y=1-x2与x轴所围成的平面区域内,做一内接矩形ABCD,其一边AB在x轴上(如图2-10所示).设AB长为2x,矩形面积为S(x).
①写出S(x)的表达式.
②求S(x)的最大值.
图 2-9
(4)(1127)在抛物线y=1-x2与x轴所围成的平面区域内,做一内接矩形ABCD,其一边AB在x轴上(如图2-10所示).设AB长为2x,矩形面积为S(x).
①写出S(x)的表达式.
②求S(x)的最大值.
【分析】 (1)解窗户的面积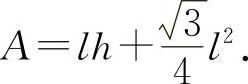
【分析】 (1)解窗户的面积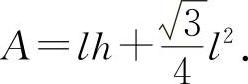
【分析】 (1)解窗户的面积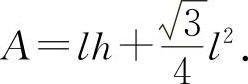
l和h满足2h+3l=12(m)得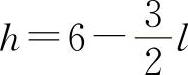 代入A.
代入A.
l和h满足2h+3l=12(m)得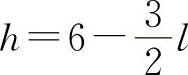 代入A.
代入A.
l和h满足2h+3l=12(m)得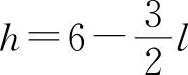 代入A.
代入A.
图 2-10
图 2-10
图 2-10
则有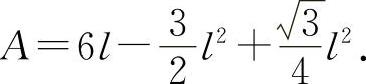
则有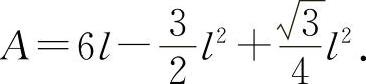
则有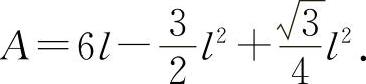
令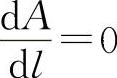 得
得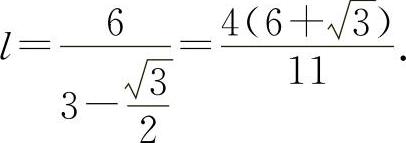
令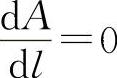 得
得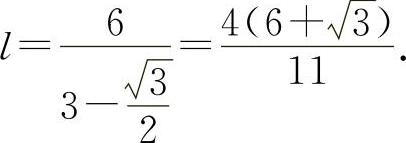
令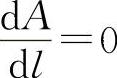 得
得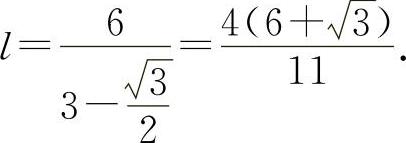
由所给问题的实际意义知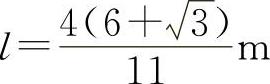 为所求.
为所求.
由所给问题的实际意义知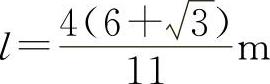 为所求.
为所求.
由所给问题的实际意义知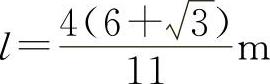 为所求.
为所求.
(2)解 ①由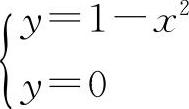 解得x=±1,
解得x=±1,
则A,B两点的坐标分别为A(-1,0),B(1,0).则|AB|=2.
(2)解 ①由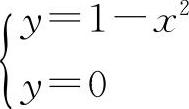 解得x=±1,
解得x=±1,
则A,B两点的坐标分别为A(-1,0),B(1,0).则|AB|=2.
(2)解 ①由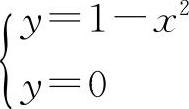 解得x=±1,
解得x=±1,
则A,B两点的坐标分别为A(-1,0),B(1,0).则|AB|=2.
②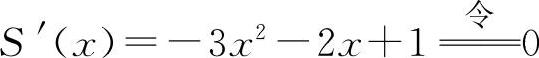 得
得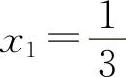 ,x2=-1(舍去).S″(x)=-6x-2,
,x2=-1(舍去).S″(x)=-6x-2,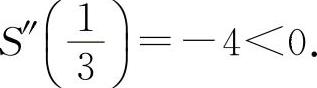
②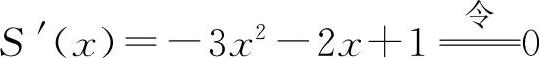 得
得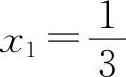 ,x2=-1(舍去).S″(x)=-6x-2,
,x2=-1(舍去).S″(x)=-6x-2,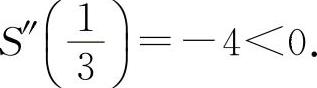
②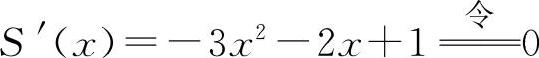 得
得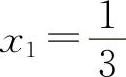 ,x2=-1(舍去).S″(x)=-6x-2,
,x2=-1(舍去).S″(x)=-6x-2,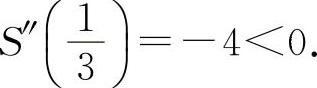
所以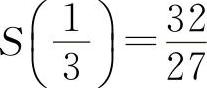 为极大值.根据实际问题,则有
为极大值.根据实际问题,则有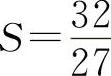 为最大值.
为最大值.
(3)解 设x轴通过半圆的直径,y轴垂直且平分直径(如图2-9所示).
所以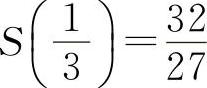 为极大值.根据实际问题,则有
为极大值.根据实际问题,则有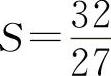 为最大值.
为最大值.
(3)解 设x轴通过半圆的直径,y轴垂直且平分直径(如图2-9所示).
所以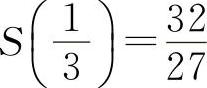 为极大值.根据实际问题,则有
为极大值.根据实际问题,则有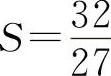 为最大值.
为最大值.
(3)解 设x轴通过半圆的直径,y轴垂直且平分直径(如图2-9所示).
设OA=x,则
设OA=x,则
设OA=x,则
矩形面积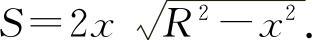
矩形面积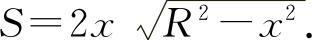
矩形面积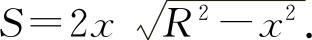
令S'=0得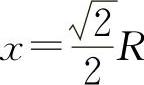 (舍去负值).
(舍去负值).
令S'=0得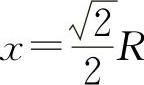 (舍去负值).
(舍去负值).
令S'=0得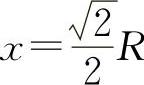 (舍去负值).
(舍去负值).
由于只有唯一驻点,根据实际问题,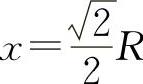 必为所求.
必为所求.
由于只有唯一驻点,根据实际问题,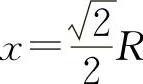 必为所求.
必为所求.
由于只有唯一驻点,根据实际问题,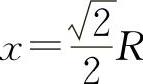 必为所求.
必为所求.
所以当矩形的长为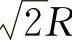 ,宽为
,宽为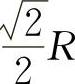 时,矩形面积最大,最大值为R2.
时,矩形面积最大,最大值为R2.
(4)解 ①S(x)=AB·BC=2xy=2x(1-x2)(0<x<1).
所以当矩形的长为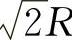 ,宽为
,宽为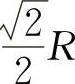 时,矩形面积最大,最大值为R2.
时,矩形面积最大,最大值为R2.
(4)解 ①S(x)=AB·BC=2xy=2x(1-x2)(0<x<1).
所以当矩形的长为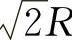 ,宽为
,宽为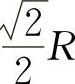 时,矩形面积最大,最大值为R2.
时,矩形面积最大,最大值为R2.
(4)解 ①S(x)=AB·BC=2xy=2x(1-x2)(0<x<1).
②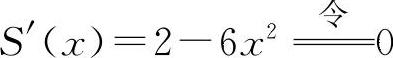 ,得
,得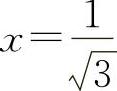 (舍去负值)
(舍去负值)
由于只有唯一驻点,所以根据实际问题,有最大值,即
②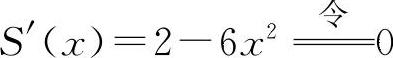 ,得
,得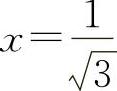 (舍去负值)
(舍去负值)
由于只有唯一驻点,所以根据实际问题,有最大值,即
②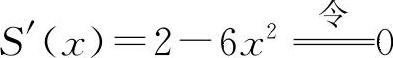 ,得
,得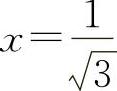 (舍去负值)
(舍去负值)
由于只有唯一驻点,所以根据实际问题,有最大值,即
当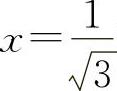 时,
时,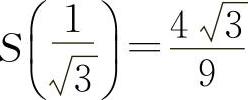 为最大值.
为最大值.
当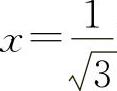 时,
时,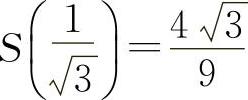 为最大值.
为最大值.
当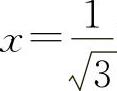 时,
时,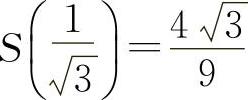 为最大值.
为最大值.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




