高等数学概念及部分考试指导

（一）概念部分

重点是导数和微分的定义，函数的可导性与连续性的关系，微分与导数的关系.

（二）运算部分

重点是基本初等函数的求导，微分公式，四则运算的求导，复合函数求导法，对数求导法等.

（三）应用部分

利用导数研究函数的性态，包括函数的单调性与极值；函数图形的凹凸性与拐点；函数曲线的渐近线以及做函数图形；最值的应用问题；利用洛必达法则求极限.

1.通常求导数运算的方法

（1）利用导数的四则运算法则.

（2）对复合函数求导利用链式法则.为了不遗漏每一个复合层次，可以由外到里一次求得一个层次的导数.

（3）对隐函数求导时，只需认作所给式子两端出现的y为中间变量，两端分别对x求导.然后整理解出y'.

（4）对数求导法，主要解决幂指函数的求导与连乘除、乘幂形式的函数求导问题.

（5）对于分段函数在分段点处的导数，通常利用定义求.

（6）求函数在某点x₀处的导数f'（x₀），通常可以先求导函数.如果导函数在x₀处有定义，则f'（x₀）即为导函数在点x₀处的函数值.若导函数在x₀处没有定义，应该利用定义求f'（x₀）.

2.利用导数判定函数增减性的通常步骤

（1）求出函数的定义域.

（2）求出f'（x）.

（3）找出f'（x）＞0时x的取值范围，即f（x）单调增加的范围.

找出f'（x）＜0时x的取值范围，即f（x）单调减少的范围.

3.利用导数判定函数y=f（x）的极值的步骤

（1）求出f（x）的驻点x_i，即f'（x_i）=0，i=1，2，…，k.

（2）求出y=f（x）有定义，但不可导的点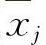，j=1，2，…，l.

（2）求出y=f（x）有定义，但不可导的点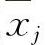，j=1，2，…，l.

（2）求出y=f（x）有定义，但不可导的点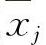，j=1，2，…，l.

（3）若在上述点的邻域内（不包含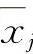）f（x）可导，可利用极值的第一充分条件判定其是否为极值点.

（4）若f″（x）存在且较易求出，可利用极值的第二充分条件判定x_i是否为极值点.

4.判定连续函数f（x）在[a，b]上最值的通常步骤

（1）若f（x）在[a，b]上可导，求出其在（a，b）内的所有驻点x_i（i=1，2，…，k）.

（3）若在上述点的邻域内（不包含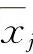）f（x）可导，可利用极值的第一充分条件判定其是否为极值点.

（4）若f″（x）存在且较易求出，可利用极值的第二充分条件判定x_i是否为极值点.

4.判定连续函数f（x）在[a，b]上最值的通常步骤

（1）若f（x）在[a，b]上可导，求出其在（a，b）内的所有驻点x_i（i=1，2，…，k）.

（3）若在上述点的邻域内（不包含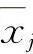）f（x）可导，可利用极值的第一充分条件判定其是否为极值点.

（4）若f″（x）存在且较易求出，可利用极值的第二充分条件判定x_i是否为极值点.

4.判定连续函数f（x）在[a，b]上最值的通常步骤

（1）若f（x）在[a，b]上可导，求出其在（a，b）内的所有驻点x_i（i=1，2，…，k）.

（2）求出f（x）在（a，b）内不可导的点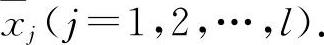

（2）求出f（x）在（a，b）内不可导的点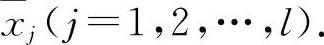

（2）求出f（x）在（a，b）内不可导的点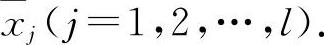(www.xing528.com)

（3）比较f（x_i）（i=1，…，k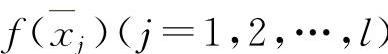），，f（a），f（b）.其中最大值即为f（x）在[a，b]上的最大值；其中最小值即为f（x）在[a，b]上的最小值.

5.判定曲线y=f（x）凹凸性及拐点的通常步骤

若曲线y=f（x）在（a，b）内的点有切线，判定其拐点的方法为：

（1）求出该函数二阶导数为零或不存在的点.

（2）若该函数的二阶导数连续（二阶导数不存在的点除外），只需判定二阶导数在上述点两侧是否异号.若在所给点x₀的两侧二阶导数异号，则（x₀，f（x₀））为曲线y=f（x）的拐点.

在f″（x）＜0的x取值范围内，曲线y=f（x）为凸的（下凹）.

在f″（x）＞0的x取值范围内，曲线y=f（x）为凹的（上凹）.

6.函数曲线渐近线的求法

（1）水平渐近线

（3）比较f（x_i）（i=1，…，k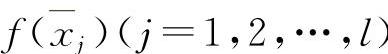），，f（a），f（b）.其中最大值即为f（x）在[a，b]上的最大值；其中最小值即为f（x）在[a，b]上的最小值.

5.判定曲线y=f（x）凹凸性及拐点的通常步骤

若曲线y=f（x）在（a，b）内的点有切线，判定其拐点的方法为：

（1）求出该函数二阶导数为零或不存在的点.

（2）若该函数的二阶导数连续（二阶导数不存在的点除外），只需判定二阶导数在上述点两侧是否异号.若在所给点x₀的两侧二阶导数异号，则（x₀，f（x₀））为曲线y=f（x）的拐点.

在f″（x）＜0的x取值范围内，曲线y=f（x）为凸的（下凹）.

在f″（x）＞0的x取值范围内，曲线y=f（x）为凹的（上凹）.

6.函数曲线渐近线的求法

（1）水平渐近线

（3）比较f（x_i）（i=1，…，k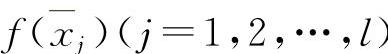），，f（a），f（b）.其中最大值即为f（x）在[a，b]上的最大值；其中最小值即为f（x）在[a，b]上的最小值.

5.判定曲线y=f（x）凹凸性及拐点的通常步骤

若曲线y=f（x）在（a，b）内的点有切线，判定其拐点的方法为：

（1）求出该函数二阶导数为零或不存在的点.

（2）若该函数的二阶导数连续（二阶导数不存在的点除外），只需判定二阶导数在上述点两侧是否异号.若在所给点x₀的两侧二阶导数异号，则（x₀，f（x₀））为曲线y=f（x）的拐点.

在f″（x）＜0的x取值范围内，曲线y=f（x）为凸的（下凹）.

在f″（x）＞0的x取值范围内，曲线y=f（x）为凹的（上凹）.

6.函数曲线渐近线的求法

（1）水平渐近线

当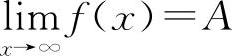时，则y=A为曲线y=f（x）的水平渐近线.

（2）铅直渐近线

当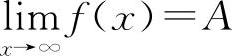时，则y=A为曲线y=f（x）的水平渐近线.

（2）铅直渐近线

当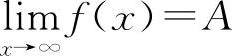时，则y=A为曲线y=f（x）的水平渐近线.

（2）铅直渐近线

当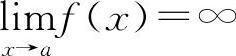时，则x=a为曲线y=f（x）的铅直渐近线.一般情况下y=f（x）的无穷间断点x=a_i均是曲线y=f（x）的铅直渐近线.例如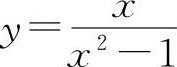，，x=±1为y的无穷间断点.此时x=±1是曲线的两条铅直渐近线.

当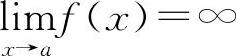时，则x=a为曲线y=f（x）的铅直渐近线.一般情况下y=f（x）的无穷间断点x=a_i均是曲线y=f（x）的铅直渐近线.例如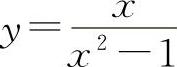，，x=±1为y的无穷间断点.此时x=±1是曲线的两条铅直渐近线.

当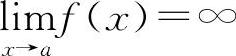时，则x=a为曲线y=f（x）的铅直渐近线.一般情况下y=f（x）的无穷间断点x=a_i均是曲线y=f（x）的铅直渐近线.例如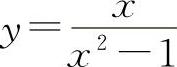，，x=±1为y的无穷间断点.此时x=±1是曲线的两条铅直渐近线.