1.【分析】用f'(x)的符号来确定单调增减区间.
(1)函数的定义域为x>0.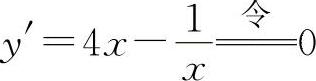 ,得驻点
,得驻点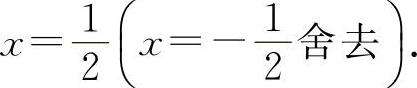
(1)函数的定义域为x>0.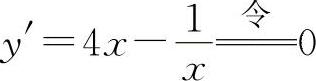 ,得驻点
,得驻点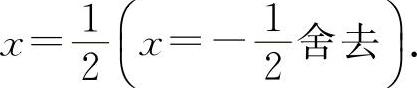
(1)函数的定义域为x>0.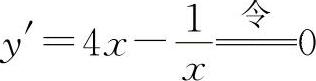 ,得驻点
,得驻点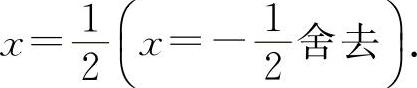
当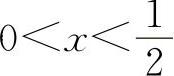 时,y'<0,所以y的单调减少区间为
时,y'<0,所以y的单调减少区间为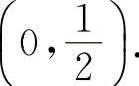
当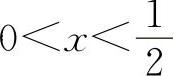 时,y'<0,所以y的单调减少区间为
时,y'<0,所以y的单调减少区间为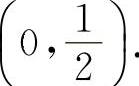
当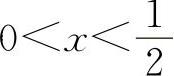 时,y'<0,所以y的单调减少区间为
时,y'<0,所以y的单调减少区间为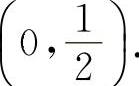
当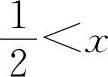 时,y'>0,所以y的单调增加区间为
时,y'>0,所以y的单调增加区间为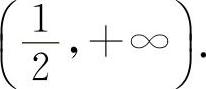
(2)函数的定义域为4x-x2≥0,解得0≤x≤4.
当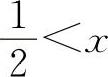 时,y'>0,所以y的单调增加区间为
时,y'>0,所以y的单调增加区间为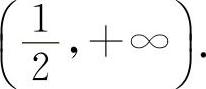
(2)函数的定义域为4x-x2≥0,解得0≤x≤4.
当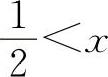 时,y'>0,所以y的单调增加区间为
时,y'>0,所以y的单调增加区间为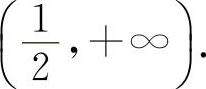
(2)函数的定义域为4x-x2≥0,解得0≤x≤4.
令y'=0,解得驻点为x=3(x=0舍去).
当0<x<3时,y'>0,所以y的单调增加区间为(0,3).
当3<x<4时,y'<0,所以y的单调减少区间为(3,4).
令y'=0,解得驻点为x=3(x=0舍去).
当0<x<3时,y'>0,所以y的单调增加区间为(0,3).
当3<x<4时,y'<0,所以y的单调减少区间为(3,4).
令y'=0,解得驻点为x=3(x=0舍去).
当0<x<3时,y'>0,所以y的单调增加区间为(0,3).
当3<x<4时,y'<0,所以y的单调减少区间为(3,4).
(3)函数的定义域为一切实数.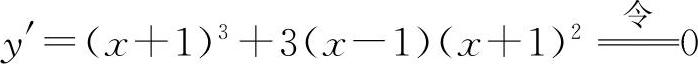 ,解得驻点
,解得驻点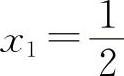 ,x2=-1.两个驻点将定义区间分为(-∞,-1),
,x2=-1.两个驻点将定义区间分为(-∞,-1),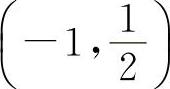 ,
,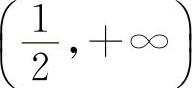 三段.
三段.
(3)函数的定义域为一切实数.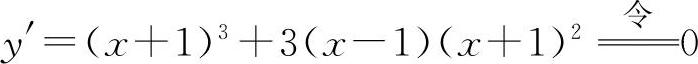 ,解得驻点
,解得驻点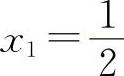 ,x2=-1.两个驻点将定义区间分为(-∞,-1),
,x2=-1.两个驻点将定义区间分为(-∞,-1),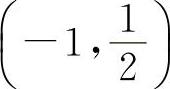 ,
,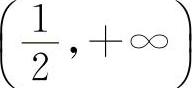 三段.
三段.
(3)函数的定义域为一切实数.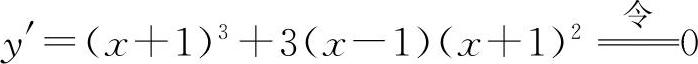 ,解得驻点
,解得驻点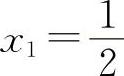 ,x2=-1.两个驻点将定义区间分为(-∞,-1),
,x2=-1.两个驻点将定义区间分为(-∞,-1),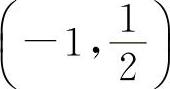 ,
,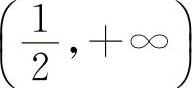 三段.
三段.
当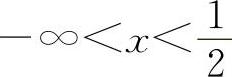 时,y'<0,所以y的单调减少区间为
时,y'<0,所以y的单调减少区间为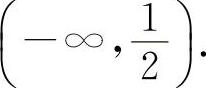
当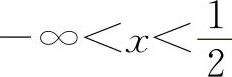 时,y'<0,所以y的单调减少区间为
时,y'<0,所以y的单调减少区间为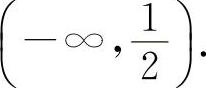
当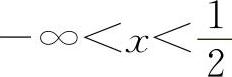 时,y'<0,所以y的单调减少区间为
时,y'<0,所以y的单调减少区间为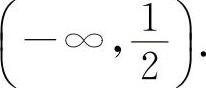
当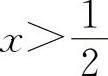 时,y'>0,所以y的单调增加区间为
时,y'>0,所以y的单调增加区间为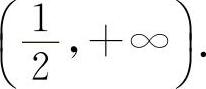
2.【分析】 求函数的极值可以用极值的第一充分条件和第二充分条件.
当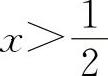 时,y'>0,所以y的单调增加区间为
时,y'>0,所以y的单调增加区间为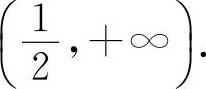
2.【分析】 求函数的极值可以用极值的第一充分条件和第二充分条件.
当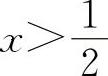 时,y'>0,所以y的单调增加区间为
时,y'>0,所以y的单调增加区间为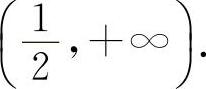
2.【分析】 求函数的极值可以用极值的第一充分条件和第二充分条件.
(1)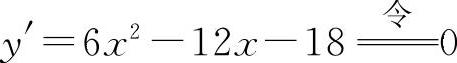 ,解得驻点x1=-1,x2=3.
,解得驻点x1=-1,x2=3.
y″=12x-12,y″(-1)=-24<0;y″(3)=24>0.
所以y(-1)=17为极大值,y(3)=-47为极小值.
(1)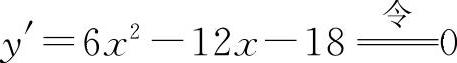 ,解得驻点x1=-1,x2=3.
,解得驻点x1=-1,x2=3.
y″=12x-12,y″(-1)=-24<0;y″(3)=24>0.
所以y(-1)=17为极大值,y(3)=-47为极小值.
(1)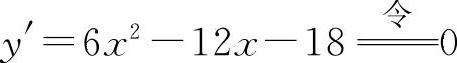 ,解得驻点x1=-1,x2=3.
,解得驻点x1=-1,x2=3.
y″=12x-12,y″(-1)=-24<0;y″(3)=24>0.
所以y(-1)=17为极大值,y(3)=-47为极小值.
(2)函数的定义域为x>-1.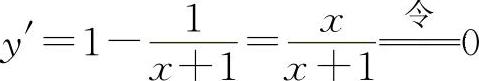 ,解得驻点x=0.
,解得驻点x=0.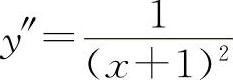 ,因为y″(0)=1>0,
,因为y″(0)=1>0,
所以y(0)=0为极小值.
3.【分析】 需求函数的y″的符号来确定凹凸区间和拐点.
(2)函数的定义域为x>-1.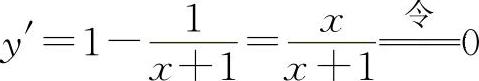 ,解得驻点x=0.
,解得驻点x=0.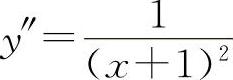 ,因为y″(0)=1>0,
,因为y″(0)=1>0,
所以y(0)=0为极小值.
3.【分析】 需求函数的y″的符号来确定凹凸区间和拐点.
(2)函数的定义域为x>-1.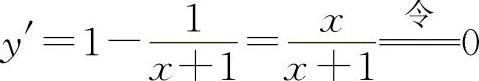 ,解得驻点x=0.
,解得驻点x=0.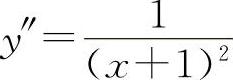 ,因为y″(0)=1>0,
,因为y″(0)=1>0,
所以y(0)=0为极小值.
3.【分析】 需求函数的y″的符号来确定凹凸区间和拐点.
当x=1时y″不存在,但当x<1时,y″<0;当x>1时,y″>0.所以凸区间为(-∞,1),凹区间为(1,+∞),点(1,2)为拐点.
当x=1时y″不存在,但当x<1时,y″<0;当x>1时,y″>0.所以凸区间为(-∞,1),凹区间为(1,+∞),点(1,2)为拐点.
当x=1时y″不存在,但当x<1时,y″<0;当x>1时,y″>0.所以凸区间为(-∞,1),凹区间为(1,+∞),点(1,2)为拐点.
(2)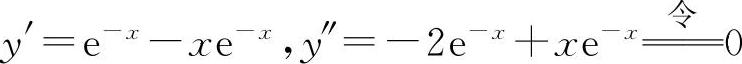 ,解得x=2.
,解得x=2.
(2)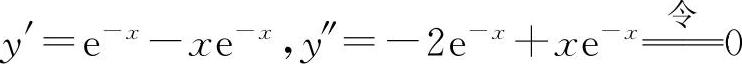 ,解得x=2.
,解得x=2.
(2)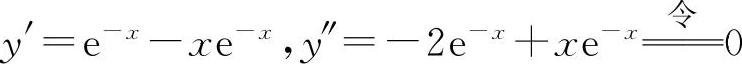 ,解得x=2.
,解得x=2.
当x<2时,y″<0;当x>2时,y″>0.所以凸区间为(-∞,2),凹区间为(2,+∞),点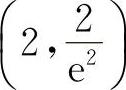 为拐点.
为拐点.
当x<2时,y″<0;当x>2时,y″>0.所以凸区间为(-∞,2),凹区间为(2,+∞),点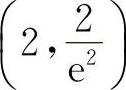 为拐点.
为拐点.
当x<2时,y″<0;当x>2时,y″>0.所以凸区间为(-∞,2),凹区间为(2,+∞),点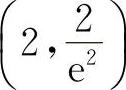 为拐点.
为拐点.
(3)y'=-2xe-x2,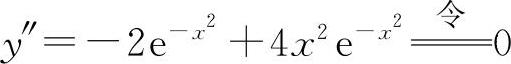 ,解得
,解得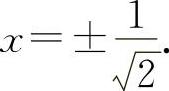
(3)y'=-2xe-x2,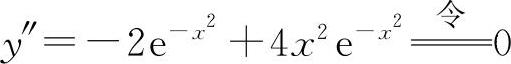 ,解得
,解得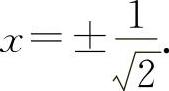
(3)y'=-2xe-x2,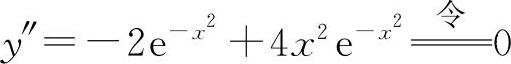 ,解得
,解得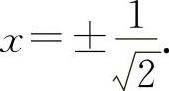
当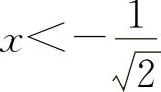 时y″>0;当
时y″>0;当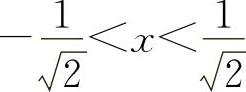 时,y″<0.
时,y″<0.
当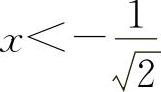 时y″>0;当
时y″>0;当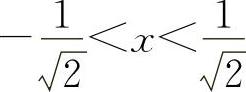 时,y″<0.
时,y″<0.
当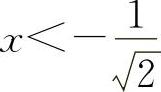 时y″>0;当
时y″>0;当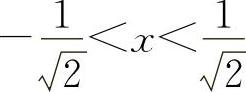 时,y″<0.
时,y″<0.
当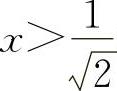 时,y″>0.所以凹区间为
时,y″>0.所以凹区间为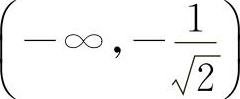 与
与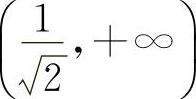 ,凸区间为
,凸区间为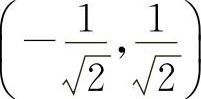 ,
,
当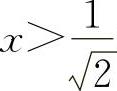 时,y″>0.所以凹区间为
时,y″>0.所以凹区间为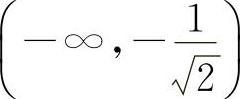 与
与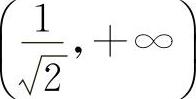 ,凸区间为
,凸区间为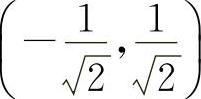 ,
,
当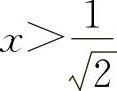 时,y″>0.所以凹区间为
时,y″>0.所以凹区间为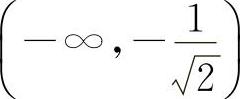 与
与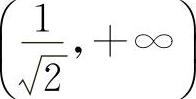 ,凸区间为
,凸区间为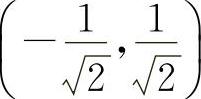 ,
,
点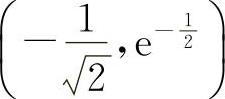 与点
与点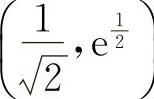 均为拐点.
均为拐点.
4.【分析】 这是导数应用的综合题,建议考生用列表法求解,既直观又简捷且不容易遗漏或混淆.
(1)函数的定义域为x≠0.
点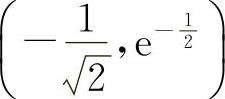 与点
与点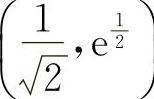 均为拐点.
均为拐点.
4.【分析】 这是导数应用的综合题,建议考生用列表法求解,既直观又简捷且不容易遗漏或混淆.
(1)函数的定义域为x≠0.
点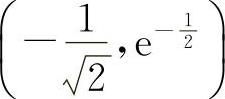 与点
与点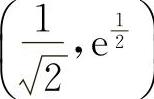 均为拐点.
均为拐点.
4.【分析】 这是导数应用的综合题,建议考生用列表法求解,既直观又简捷且不容易遗漏或混淆.
(1)函数的定义域为x≠0.
令y'=0 得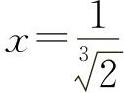 ;令y″=0得x=-1.列表如表2-3所示.
;令y″=0得x=-1.列表如表2-3所示.
表 2-3
表 2-3
令y'=0 得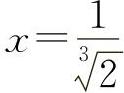 ;令y″=0得x=-1.列表如表2-3所示.
;令y″=0得x=-1.列表如表2-3所示.
表 2-3
所以函数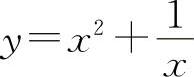 的单调减少区间为(-∞,0)与
的单调减少区间为(-∞,0)与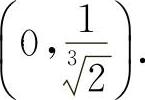
所以函数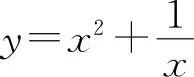 的单调减少区间为(-∞,0)与
的单调减少区间为(-∞,0)与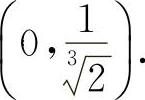
所以函数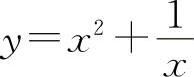 的单调减少区间为(-∞,0)与
的单调减少区间为(-∞,0)与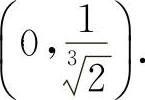
函数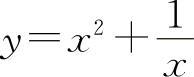 的单调增加区间为
的单调增加区间为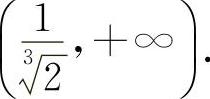
函数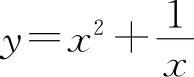 的单调增加区间为
的单调增加区间为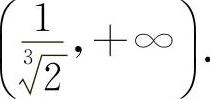
函数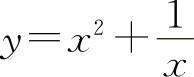 的单调增加区间为
的单调增加区间为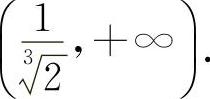
函数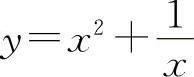 的极小值为
的极小值为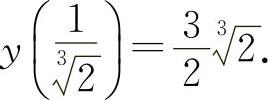
函数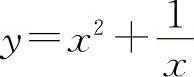 的极小值为
的极小值为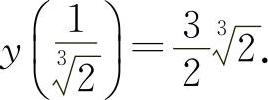
函数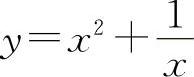 的极小值为
的极小值为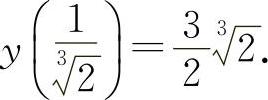
曲线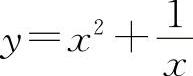 的凹区间为(-∞,-1)与(0,+∞).
的凹区间为(-∞,-1)与(0,+∞).
曲线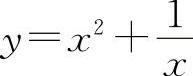 的凹区间为(-∞,-1)与(0,+∞).
的凹区间为(-∞,-1)与(0,+∞).
曲线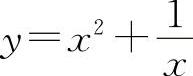 的凹区间为(-∞,-1)与(0,+∞).
的凹区间为(-∞,-1)与(0,+∞).
曲线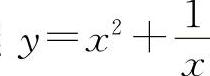 的凸区间为(-1,0);曲线
的凸区间为(-1,0);曲线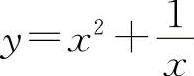 的拐点为(-1,0).
的拐点为(-1,0).
(2)定义域为一切实数.
曲线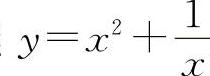 的凸区间为(-1,0);曲线
的凸区间为(-1,0);曲线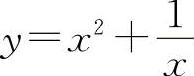 的拐点为(-1,0).
的拐点为(-1,0).
(2)定义域为一切实数.
曲线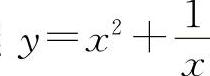 的凸区间为(-1,0);曲线
的凸区间为(-1,0);曲线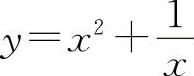 的拐点为(-1,0).
的拐点为(-1,0).
(2)定义域为一切实数.
令y'=0,解得驻点x=±1.
令y'=0,解得驻点x=±1.(https://www.xing528.com)
令y'=0,解得驻点x=±1.
令y″=0,解得x=0,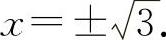 列表如表2-4所示.
列表如表2-4所示.
表 2-4
令y″=0,解得x=0,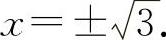 列表如表2-4所示.
列表如表2-4所示.
表 2-4
令y″=0,解得x=0,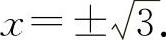 列表如表2-4所示.
列表如表2-4所示.
表 2-4
所以函数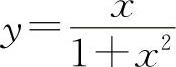 的单调减少区间为(-∞,-1)与(1,+∞).
的单调减少区间为(-∞,-1)与(1,+∞).
所以函数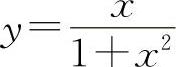 的单调减少区间为(-∞,-1)与(1,+∞).
的单调减少区间为(-∞,-1)与(1,+∞).
所以函数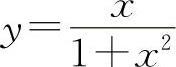 的单调减少区间为(-∞,-1)与(1,+∞).
的单调减少区间为(-∞,-1)与(1,+∞).
函数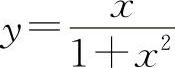 的单调增加区间为(-1,1).
的单调增加区间为(-1,1).
函数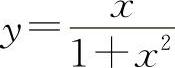 的单调增加区间为(-1,1).
的单调增加区间为(-1,1).
函数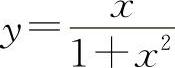 的单调增加区间为(-1,1).
的单调增加区间为(-1,1).
函数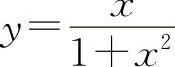 的极小值为
的极小值为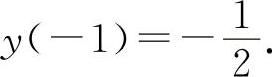
函数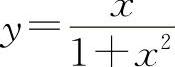 的极小值为
的极小值为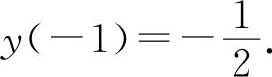
函数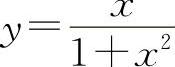 的极小值为
的极小值为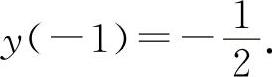
函数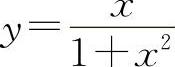 的极大值为
的极大值为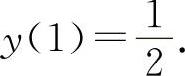
函数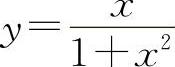 的极大值为
的极大值为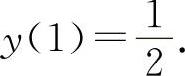
函数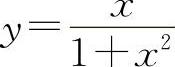 的极大值为
的极大值为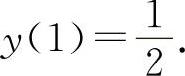
曲线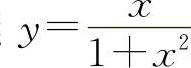 的凸区间为
的凸区间为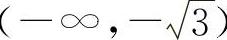 与
与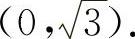
曲线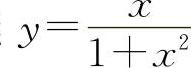 的凸区间为
的凸区间为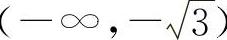 与
与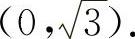
曲线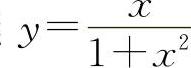 的凸区间为
的凸区间为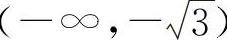 与
与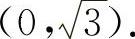
曲线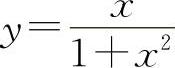 的凹区间为
的凹区间为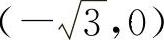 与
与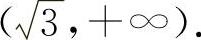
曲线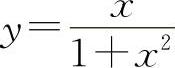 的凹区间为
的凹区间为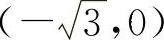 与
与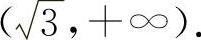
曲线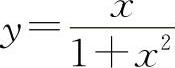 的凹区间为
的凹区间为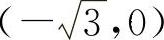 与
与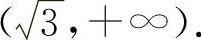
曲线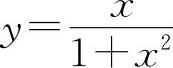 的拐点为
的拐点为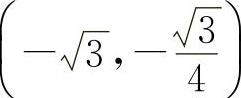 ,(0,0),
,(0,0),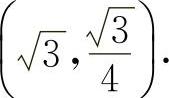
由于题(2)的极值点有2个,拐点有3个,用列表法的优越性就显而易见了.
5.【分析】 这里的两个不等式都可用函数的单调性得到证明.
曲线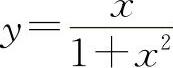 的拐点为
的拐点为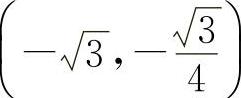 ,(0,0),
,(0,0),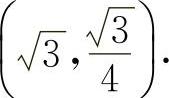
由于题(2)的极值点有2个,拐点有3个,用列表法的优越性就显而易见了.
5.【分析】 这里的两个不等式都可用函数的单调性得到证明.
曲线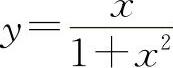 的拐点为
的拐点为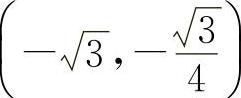 ,(0,0),
,(0,0),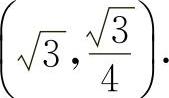
由于题(2)的极值点有2个,拐点有3个,用列表法的优越性就显而易见了.
5.【分析】 这里的两个不等式都可用函数的单调性得到证明.
证明 (1)设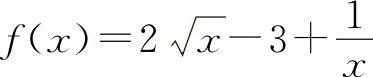 ,则
,则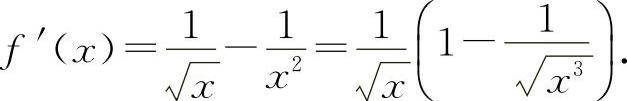
证明 (1)设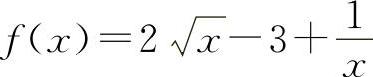 ,则
,则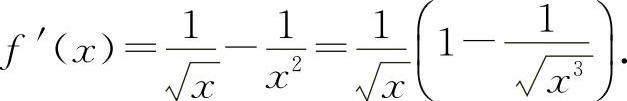
证明 (1)设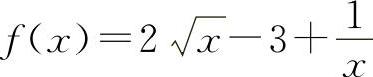 ,则
,则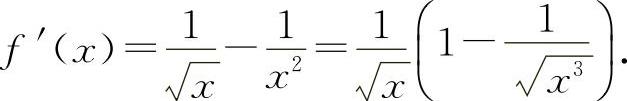
当x>1时,f'(x)>0,所以f(x)单调增加,所以当x>1时,f(x)>f(1)=0,即 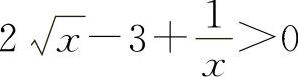 ,得
,得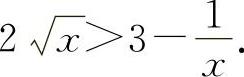
当x>1时,f'(x)>0,所以f(x)单调增加,所以当x>1时,f(x)>f(1)=0,即 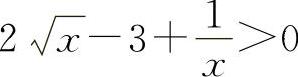 ,得
,得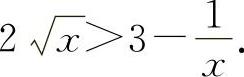
当x>1时,f'(x)>0,所以f(x)单调增加,所以当x>1时,f(x)>f(1)=0,即 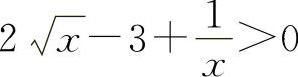 ,得
,得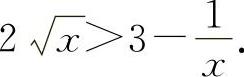
(2)设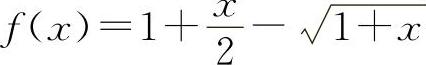 ,则
,则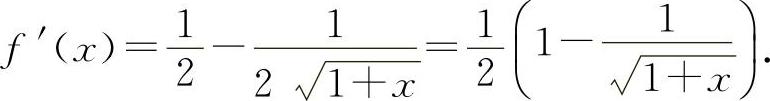
(2)设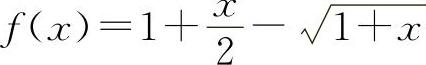 ,则
,则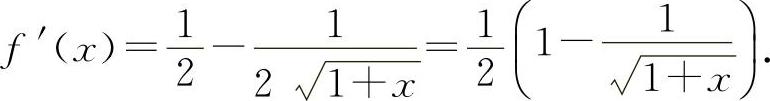
(2)设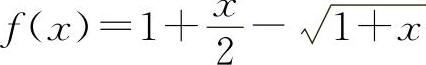 ,则
,则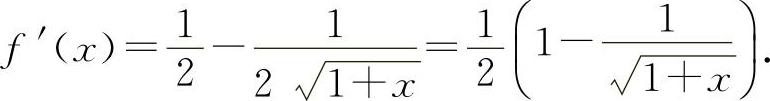
当x>0时,f'(x)>0,所以f(x)单调增加.所以当x>0时,f(x)>f(0)=0,即 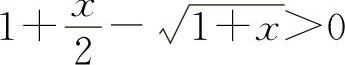 得
得 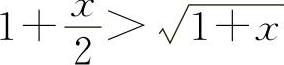
6.【分析】 利用可导函数在x0处有极值的f'(x0)=0可求得a和b.
当x>0时,f'(x)>0,所以f(x)单调增加.所以当x>0时,f(x)>f(0)=0,即 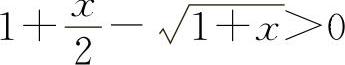 得
得 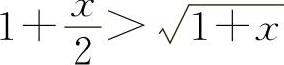
6.【分析】 利用可导函数在x0处有极值的f'(x0)=0可求得a和b.
当x>0时,f'(x)>0,所以f(x)单调增加.所以当x>0时,f(x)>f(0)=0,即 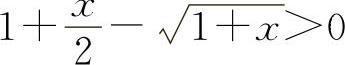 得
得 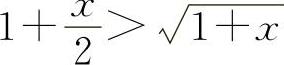
6.【分析】 利用可导函数在x0处有极值的f'(x0)=0可求得a和b.
解 因为 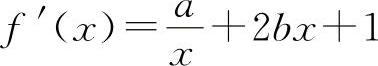 ,则有
,则有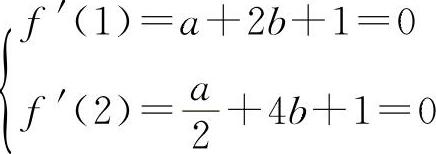
解 因为 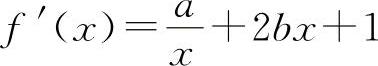 ,则有
,则有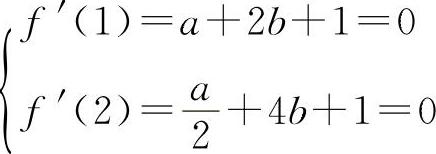
解 因为 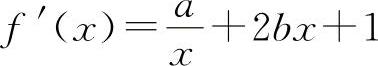 ,则有
,则有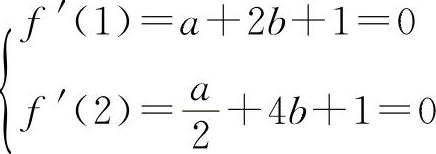
解得 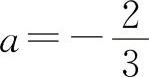 ,
,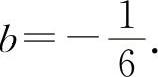
7.【分析】 可导函数在拐点处的f″(x0)=0.并利用f(1)=3可求得a和b.
解 因为 f(1)=3 即 a+b=3.
f″(x)=6ax+2b,f″(1)=6a+2b=0.
解得 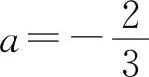 ,
,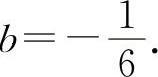
7.【分析】 可导函数在拐点处的f″(x0)=0.并利用f(1)=3可求得a和b.
解 因为 f(1)=3 即 a+b=3.
f″(x)=6ax+2b,f″(1)=6a+2b=0.
解得 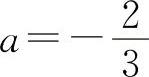 ,
,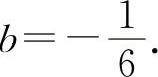
7.【分析】 可导函数在拐点处的f″(x0)=0.并利用f(1)=3可求得a和b.
解 因为 f(1)=3 即 a+b=3.
f″(x)=6ax+2b,f″(1)=6a+2b=0.
解得 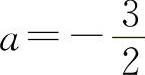 ,
,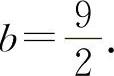
8.【分析】 这是应用题中的最值问题,首先要列出需求的函数关系式,再求其在已知条件下的最值问题.本题的围墙高度可设为一个单位高度.
解得 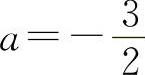 ,
,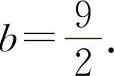
8.【分析】 这是应用题中的最值问题,首先要列出需求的函数关系式,再求其在已知条件下的最值问题.本题的围墙高度可设为一个单位高度.
解得 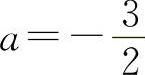 ,
,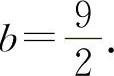
8.【分析】 这是应用题中的最值问题,首先要列出需求的函数关系式,再求其在已知条件下的最值问题.本题的围墙高度可设为一个单位高度.
解 设围墙的长为x,宽为y,且xy=216,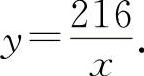 中间隔断的围墙应为宽y,则有围墙的面积为
中间隔断的围墙应为宽y,则有围墙的面积为
解 设围墙的长为x,宽为y,且xy=216,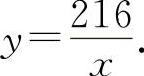 中间隔断的围墙应为宽y,则有围墙的面积为
中间隔断的围墙应为宽y,则有围墙的面积为
解 设围墙的长为x,宽为y,且xy=216,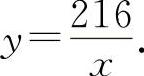 中间隔断的围墙应为宽y,则有围墙的面积为
中间隔断的围墙应为宽y,则有围墙的面积为
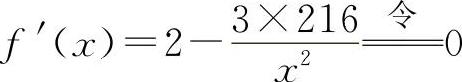 ,解得x=18(x=-18舍去).由于只有一个极值点,它必为所求,所以围墙的长为18m、宽为12m时,其建筑费用为最少.
,解得x=18(x=-18舍去).由于只有一个极值点,它必为所求,所以围墙的长为18m、宽为12m时,其建筑费用为最少.
9.【分析】 本题实际是求窗的面积为最大时的圆半径r和矩形高h的值.
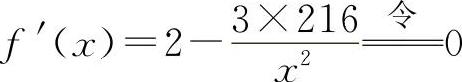 ,解得x=18(x=-18舍去).由于只有一个极值点,它必为所求,所以围墙的长为18m、宽为12m时,其建筑费用为最少.
,解得x=18(x=-18舍去).由于只有一个极值点,它必为所求,所以围墙的长为18m、宽为12m时,其建筑费用为最少.
9.【分析】 本题实际是求窗的面积为最大时的圆半径r和矩形高h的值.
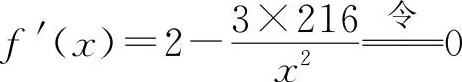 ,解得x=18(x=-18舍去).由于只有一个极值点,它必为所求,所以围墙的长为18m、宽为12m时,其建筑费用为最少.
,解得x=18(x=-18舍去).由于只有一个极值点,它必为所求,所以围墙的长为18m、宽为12m时,其建筑费用为最少.
9.【分析】 本题实际是求窗的面积为最大时的圆半径r和矩形高h的值.
解 设窗的面积为A,则有 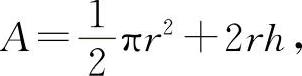
满足条件 l=πr+2r+2h,
解 设窗的面积为A,则有 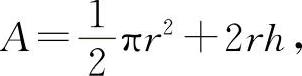
满足条件 l=πr+2r+2h,
解 设窗的面积为A,则有 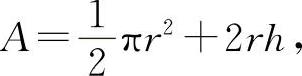
满足条件 l=πr+2r+2h,
解出 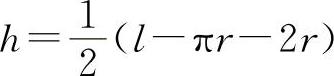
解出 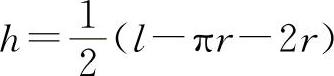
解出 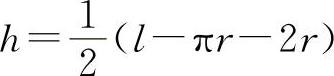
代入A中得 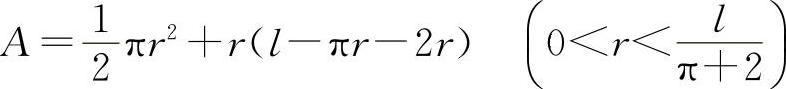
则 A'(r)=πr+l-2(π+2)r=l-(π+4)r
代入A中得 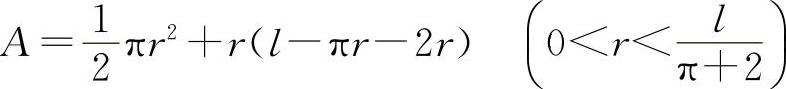
则 A'(r)=πr+l-2(π+2)r=l-(π+4)r
代入A中得 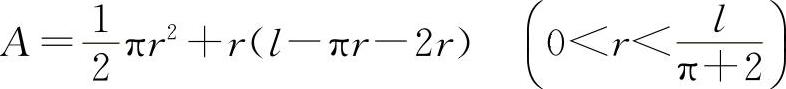
则 A'(r)=πr+l-2(π+2)r=l-(π+4)r
令 A'(r)=0 解得 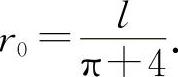
令 A'(r)=0 解得 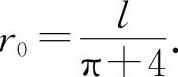
令 A'(r)=0 解得 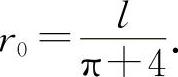
由于此问题只有唯一的驻点,所以它必为所求,因此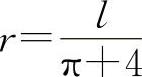 ,且有
,且有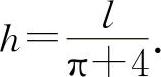 即
即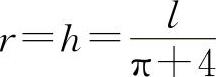 时,所通过的光线最为充足(见图2-6).
时,所通过的光线最为充足(见图2-6).
由于此问题只有唯一的驻点,所以它必为所求,因此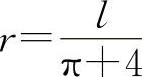 ,且有
,且有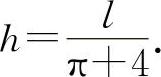 即
即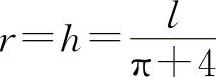 时,所通过的光线最为充足(见图2-6).
时,所通过的光线最为充足(见图2-6).
由于此问题只有唯一的驻点,所以它必为所求,因此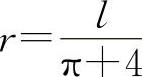 ,且有
,且有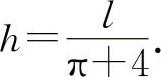 即
即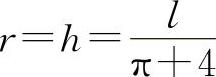 时,所通过的光线最为充足(见图2-6).
时,所通过的光线最为充足(见图2-6).
图 2-6
图 2-6
图 2-6
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




