1.选D选项 【分析】 由于A、B、C选项均为基本初等函数,所以均可导,所以排除A、B、C选项.所以应选D选项.
事实上,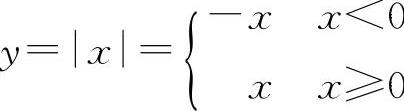 ,其左导数y'-=-1,右导数y'+=1,由于y'-≠y'+,所以在x=0处不可导.
,其左导数y'-=-1,右导数y'+=1,由于y'-≠y'+,所以在x=0处不可导.
事实上,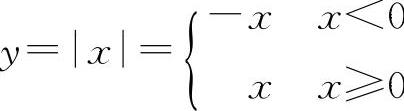 ,其左导数y'-=-1,右导数y'+=1,由于y'-≠y'+,所以在x=0处不可导.
,其左导数y'-=-1,右导数y'+=1,由于y'-≠y'+,所以在x=0处不可导.
事实上,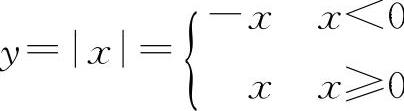 ,其左导数y'-=-1,右导数y'+=1,由于y'-≠y'+,所以在x=0处不可导.
,其左导数y'-=-1,右导数y'+=1,由于y'-≠y'+,所以在x=0处不可导.
2.选B选项 【分析】 对选项A,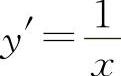 ,在x=0处y'|x=0不存在,所以排除A选项.很多考生往往会选A选项,认为它是基本初等函数,所以可导.其错误原因是忽略了y=lnx的定义域为x>0,而x=0时,lnx不存在.
,在x=0处y'|x=0不存在,所以排除A选项.很多考生往往会选A选项,认为它是基本初等函数,所以可导.其错误原因是忽略了y=lnx的定义域为x>0,而x=0时,lnx不存在.
2.选B选项 【分析】 对选项A,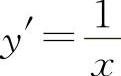 ,在x=0处y'|x=0不存在,所以排除A选项.很多考生往往会选A选项,认为它是基本初等函数,所以可导.其错误原因是忽略了y=lnx的定义域为x>0,而x=0时,lnx不存在.
,在x=0处y'|x=0不存在,所以排除A选项.很多考生往往会选A选项,认为它是基本初等函数,所以可导.其错误原因是忽略了y=lnx的定义域为x>0,而x=0时,lnx不存在.
2.选B选项 【分析】 对选项A,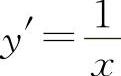 ,在x=0处y'|x=0不存在,所以排除A选项.很多考生往往会选A选项,认为它是基本初等函数,所以可导.其错误原因是忽略了y=lnx的定义域为x>0,而x=0时,lnx不存在.
,在x=0处y'|x=0不存在,所以排除A选项.很多考生往往会选A选项,认为它是基本初等函数,所以可导.其错误原因是忽略了y=lnx的定义域为x>0,而x=0时,lnx不存在.
对选项B,由于在x=0处的导数是其邻域的函数的变化率,而在x=0的某个邻域如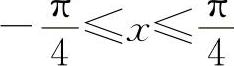 内,y=|cosx|=cosx,此时
内,y=|cosx|=cosx,此时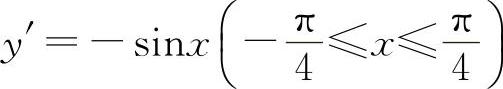 ,所以y'|x=0=0,应选B选项.
,所以y'|x=0=0,应选B选项.
由于选项B正确,且题目为单项选择,所以选项C和D肯定不正确,无须验证(考生也可自行验证其导数在x=0处不存在).
3.选C选项 【分析】 利用可导必连续的条件以及在分段点处的连续可导条件,即可求得a和b.
由连续定义:f(0-0)=f(0+0)=f(0)得e0=a=1.
由可导定义:f'-(0)=f'+(0)得2e2x|x=0=-b,则b=-2.
所以应选C选项.
对选项B,由于在x=0处的导数是其邻域的函数的变化率,而在x=0的某个邻域如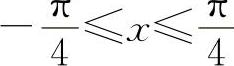 内,y=|cosx|=cosx,此时
内,y=|cosx|=cosx,此时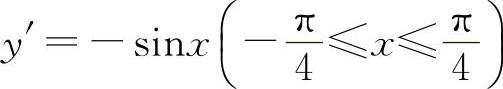 ,所以y'|x=0=0,应选B选项.
,所以y'|x=0=0,应选B选项.
由于选项B正确,且题目为单项选择,所以选项C和D肯定不正确,无须验证(考生也可自行验证其导数在x=0处不存在).
3.选C选项 【分析】 利用可导必连续的条件以及在分段点处的连续可导条件,即可求得a和b.
由连续定义:f(0-0)=f(0+0)=f(0)得e0=a=1.
由可导定义:f'-(0)=f'+(0)得2e2x|x=0=-b,则b=-2.
所以应选C选项.
对选项B,由于在x=0处的导数是其邻域的函数的变化率,而在x=0的某个邻域如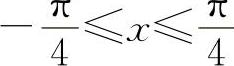 内,y=|cosx|=cosx,此时
内,y=|cosx|=cosx,此时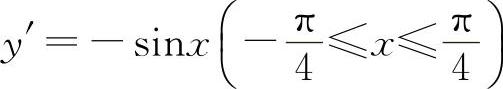 ,所以y'|x=0=0,应选B选项.
,所以y'|x=0=0,应选B选项.
由于选项B正确,且题目为单项选择,所以选项C和D肯定不正确,无须验证(考生也可自行验证其导数在x=0处不存在).
3.选C选项 【分析】 利用可导必连续的条件以及在分段点处的连续可导条件,即可求得a和b.
由连续定义:f(0-0)=f(0+0)=f(0)得e0=a=1.
由可导定义:f'-(0)=f'+(0)得2e2x|x=0=-b,则b=-2.
所以应选C选项.
4.【分析】 利用导数的定义的结构式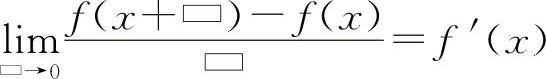 求解.
求解.
4.【分析】 利用导数的定义的结构式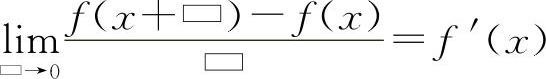 求解.
求解.
4.【分析】 利用导数的定义的结构式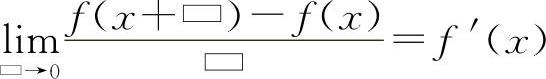 求解.
求解.
解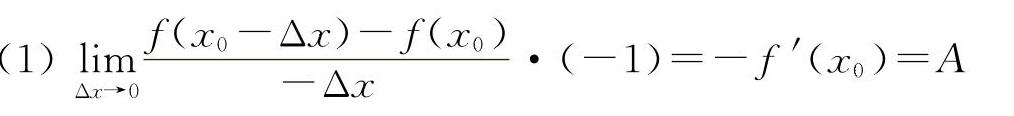
解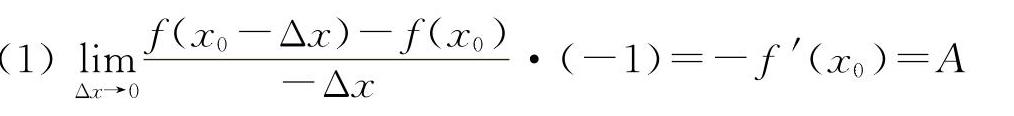
解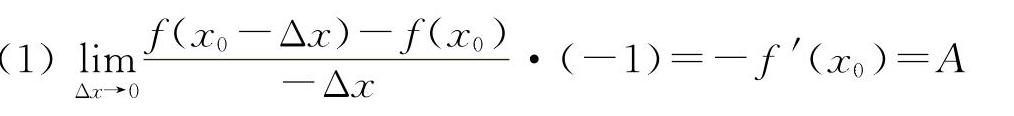
5.选C选项 【分析】 方法同题4(1),则有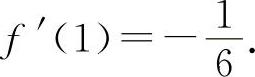 所以应选C选项.
所以应选C选项.
6.选A选项 【分析】 当x=0时,y=1,又过点x=0的切线斜率为y'|x=0=(1+ex)x=0=2,用点斜式得切线方程为y-1=2(x-0)即2x-y+1=0.所以应选A选项.
5.选C选项 【分析】 方法同题4(1),则有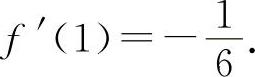 所以应选C选项.
所以应选C选项.
6.选A选项 【分析】 当x=0时,y=1,又过点x=0的切线斜率为y'|x=0=(1+ex)x=0=2,用点斜式得切线方程为y-1=2(x-0)即2x-y+1=0.所以应选A选项.
5.选C选项 【分析】 方法同题4(1),则有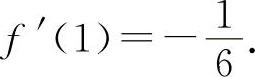 所以应选C选项.
所以应选C选项.
6.选A选项 【分析】 当x=0时,y=1,又过点x=0的切线斜率为y'|x=0=(1+ex)x=0=2,用点斜式得切线方程为y-1=2(x-0)即2x-y+1=0.所以应选A选项.
7.填 【分析】 利用导数的几何意义表示在点x处切线的斜率.即y'=tanα=k1,切线与已知直线平行,则有k1=k2,所以y'=4x-1=4,得
【分析】 利用导数的几何意义表示在点x处切线的斜率.即y'=tanα=k1,切线与已知直线平行,则有k1=k2,所以y'=4x-1=4,得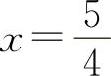 ,代入y=2x2-x-2,得
,代入y=2x2-x-2,得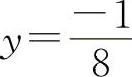 ,所以应填
,所以应填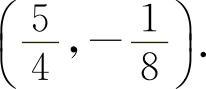
7.填 【分析】 利用导数的几何意义表示在点x处切线的斜率.即y'=tanα=k1,切线与已知直线平行,则有k1=k2,所以y'=4x-1=4,得
【分析】 利用导数的几何意义表示在点x处切线的斜率.即y'=tanα=k1,切线与已知直线平行,则有k1=k2,所以y'=4x-1=4,得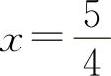 ,代入y=2x2-x-2,得
,代入y=2x2-x-2,得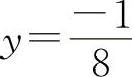 ,所以应填
,所以应填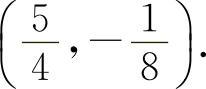
7.填 【分析】 利用导数的几何意义表示在点x处切线的斜率.即y'=tanα=k1,切线与已知直线平行,则有k1=k2,所以y'=4x-1=4,得
【分析】 利用导数的几何意义表示在点x处切线的斜率.即y'=tanα=k1,切线与已知直线平行,则有k1=k2,所以y'=4x-1=4,得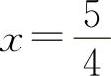 ,代入y=2x2-x-2,得
,代入y=2x2-x-2,得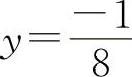 ,所以应填
,所以应填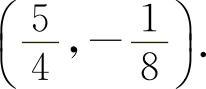
8.解 (1)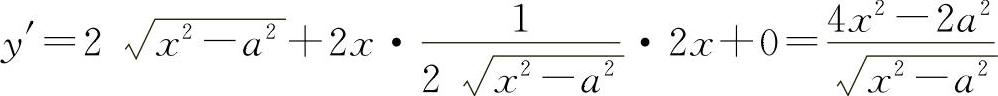
8.解 (1)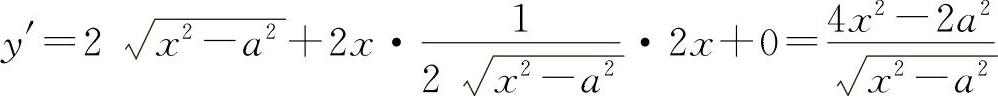
8.解 (1)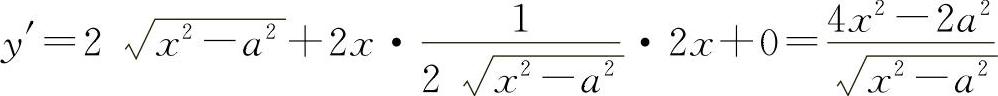
注:如写成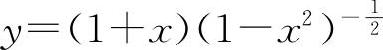 再求y'亦为简单.商的导数经常可以用乘积的导数计算.
再求y'亦为简单.商的导数经常可以用乘积的导数计算.
注:如写成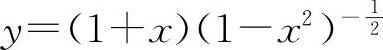 再求y'亦为简单.商的导数经常可以用乘积的导数计算.
再求y'亦为简单.商的导数经常可以用乘积的导数计算.
注:如写成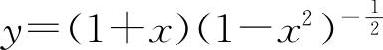 再求y'亦为简单.商的导数经常可以用乘积的导数计算.
再求y'亦为简单.商的导数经常可以用乘积的导数计算.
(4)【分析】该题一定要注意中间变量.
(4)【分析】该题一定要注意中间变量.
(4)【分析】该题一定要注意中间变量.
解 令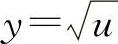 ,
,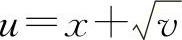 ,
,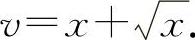
解 令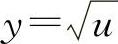 ,
,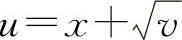 ,
,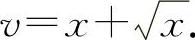
解 令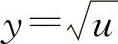 ,
,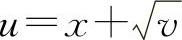 ,
,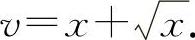
则 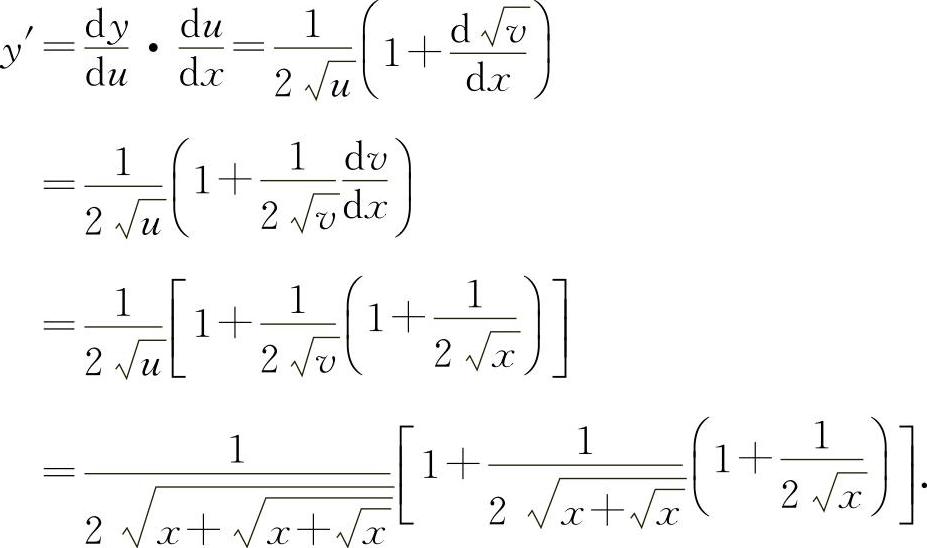
则 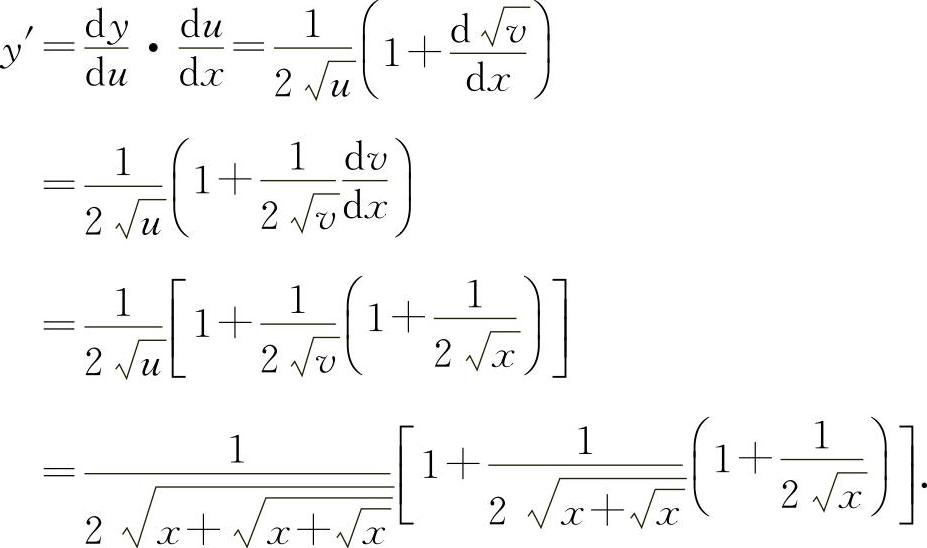
则 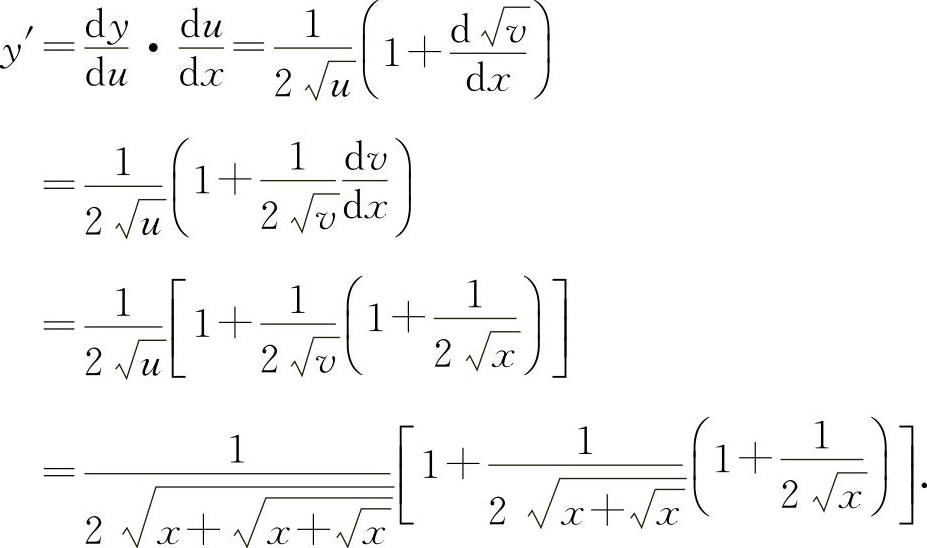
9.(1)两边取对数得 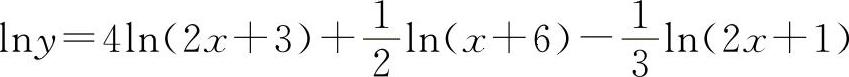
9.(1)两边取对数得 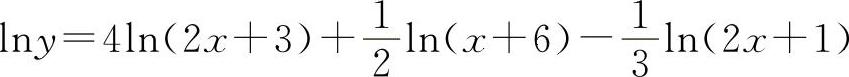
9.(1)两边取对数得 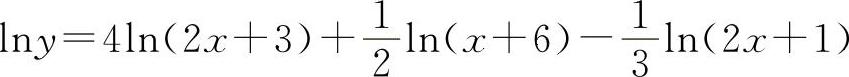
两边对x求导得 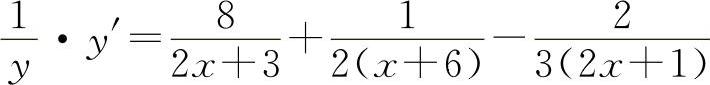
两边对x求导得 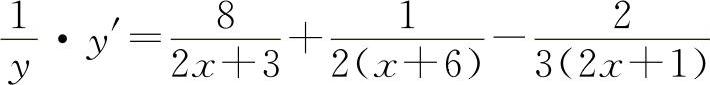
两边对x求导得 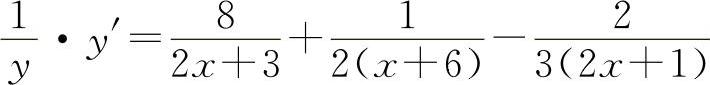
所以 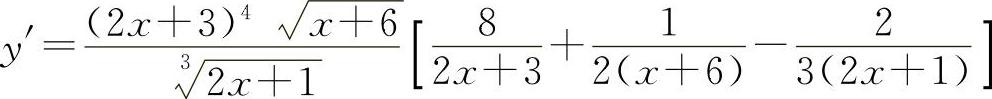
(2)两边取对数得 lny=x[lnx-ln(1+x2)]
所以 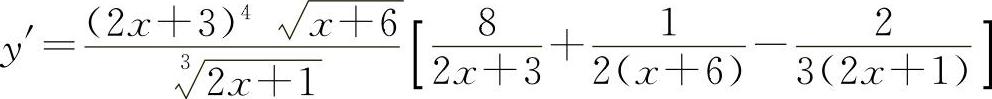
(2)两边取对数得 lny=x[lnx-ln(1+x2)]
所以 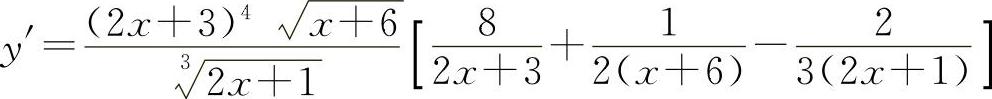
(2)两边取对数得 lny=x[lnx-ln(1+x2)]
两边对x求导得 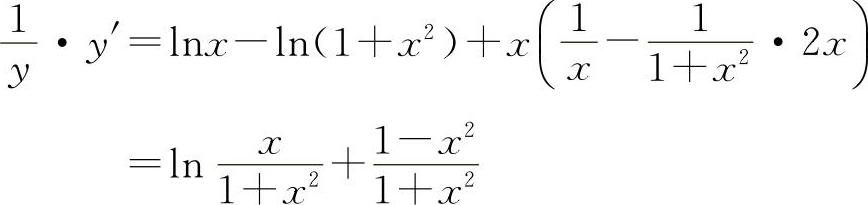
两边对x求导得 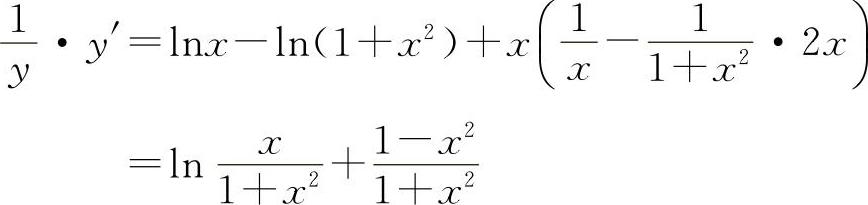
两边对x求导得 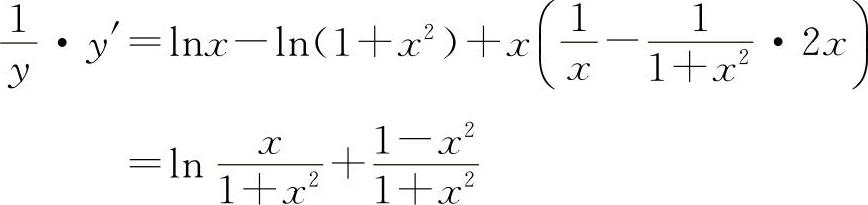
所以 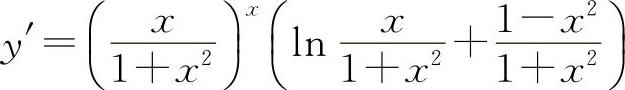
10.【分析】 隐函数求导的关键是将y看成x的复合函数对x求导.
所以 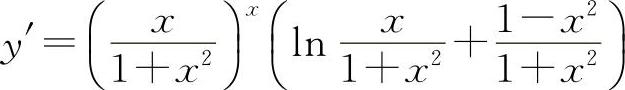
10.【分析】 隐函数求导的关键是将y看成x的复合函数对x求导.
所以 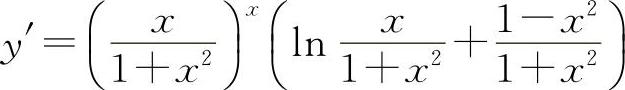 (https://www.xing528.com)
(https://www.xing528.com)
10.【分析】 隐函数求导的关键是将y看成x的复合函数对x求导.
(1)两边对x求导得y'sinx+ycosx+sin(x-y)(1-y')=0解得 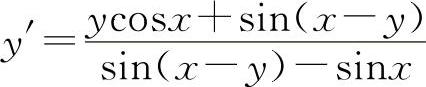
(1)两边对x求导得y'sinx+ycosx+sin(x-y)(1-y')=0解得 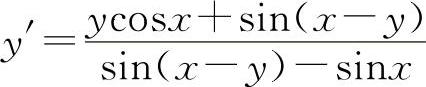
(1)两边对x求导得y'sinx+ycosx+sin(x-y)(1-y')=0解得 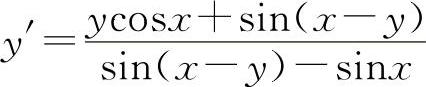
(2)两边对x求导得 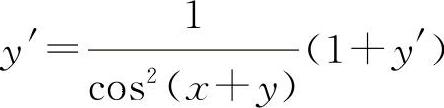
(2)两边对x求导得 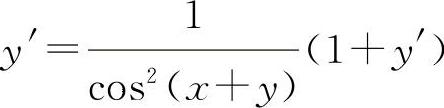
(2)两边对x求导得 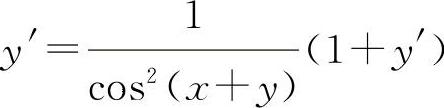
解得 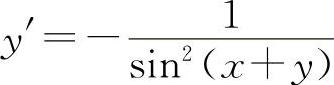
(3)两边对x求导得 2x+2yy'=exy(y+xy')
解得 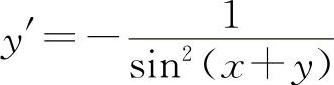
(3)两边对x求导得 2x+2yy'=exy(y+xy')
解得 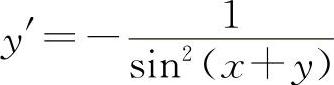
(3)两边对x求导得 2x+2yy'=exy(y+xy')
解得 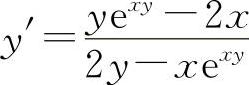
(4)两边对x求导得 ex+y(1+y')-sin(xy)(y+xy')=0
解得 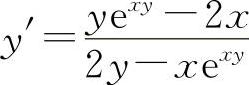
(4)两边对x求导得 ex+y(1+y')-sin(xy)(y+xy')=0
解得 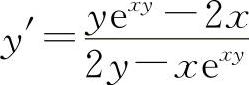
(4)两边对x求导得 ex+y(1+y')-sin(xy)(y+xy')=0
解得 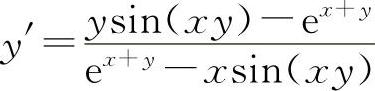
11.【分析】 先求y',尽可能化简后再求y″.
解 (1)y'=3x2lnx+x2=x2(3lnx+1)
所以 y″=2x(3lnx+1)+3x=x(6lnx+5)
解得 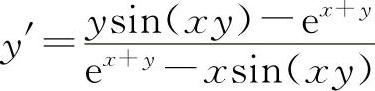
11.【分析】 先求y',尽可能化简后再求y″.
解 (1)y'=3x2lnx+x2=x2(3lnx+1)
所以 y″=2x(3lnx+1)+3x=x(6lnx+5)
解得 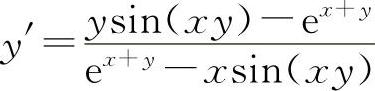
11.【分析】 先求y',尽可能化简后再求y″.
解 (1)y'=3x2lnx+x2=x2(3lnx+1)
所以 y″=2x(3lnx+1)+3x=x(6lnx+5)
所以 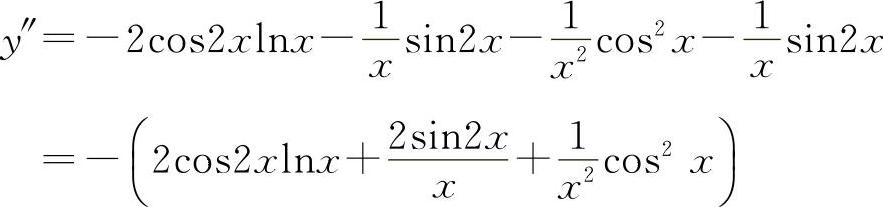
12.【分析】 求函数的微分通常可求y'再求dy,也可直接求微分,计算过程请考生自行完成.
所以 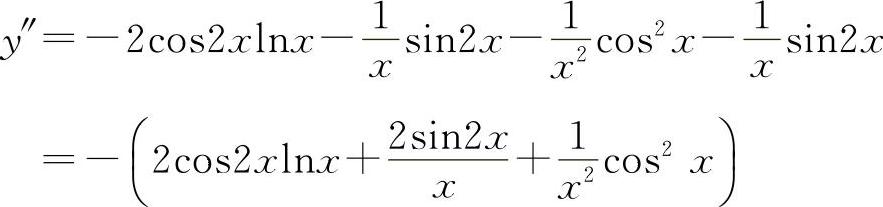
12.【分析】 求函数的微分通常可求y'再求dy,也可直接求微分,计算过程请考生自行完成.
所以 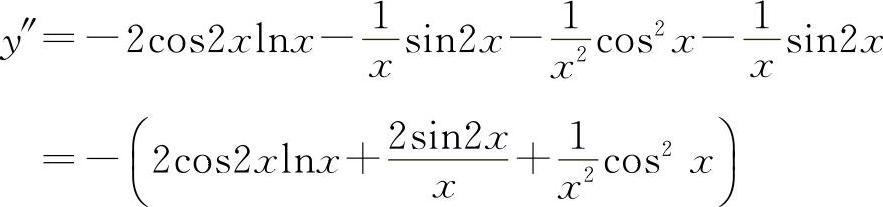
12.【分析】 求函数的微分通常可求y'再求dy,也可直接求微分,计算过程请考生自行完成.
13.【分析】 这是微分的逆运算,这在后面的不定积分计算中应用较多,希望考生熟练掌握.
13.【分析】 这是微分的逆运算,这在后面的不定积分计算中应用较多,希望考生熟练掌握.
13.【分析】 这是微分的逆运算,这在后面的不定积分计算中应用较多,希望考生熟练掌握.
(1)2x (2)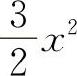 (3)sint
(3)sint
(1)2x (2)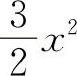 (3)sint
(3)sint
(1)2x (2)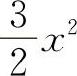 (3)sint
(3)sint
(4)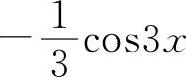 (5)ln(1+u) (6)
(5)ln(1+u) (6)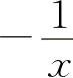
(4)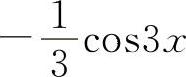 (5)ln(1+u) (6)
(5)ln(1+u) (6)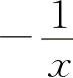
(4)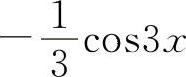 (5)ln(1+u) (6)
(5)ln(1+u) (6)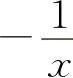
(7)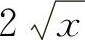 (8)tanx (9)arcsinx
(8)tanx (9)arcsinx
(10)arctanx
(7)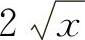 (8)tanx (9)arcsinx
(8)tanx (9)arcsinx
(10)arctanx
(7)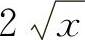 (8)tanx (9)arcsinx
(8)tanx (9)arcsinx
(10)arctanx
14.【分析】 先用复合函数的求导公式计算,然后再求出f'(x)及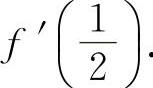
14.【分析】 先用复合函数的求导公式计算,然后再求出f'(x)及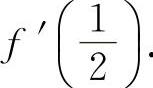
14.【分析】 先用复合函数的求导公式计算,然后再求出f'(x)及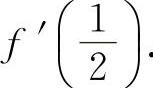
解 因为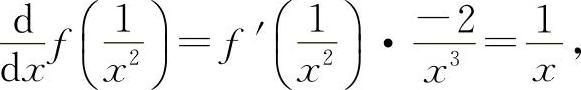
解 因为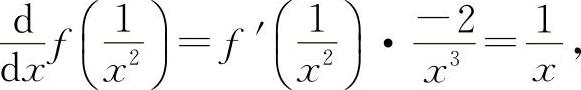
解 因为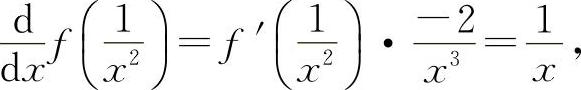
即 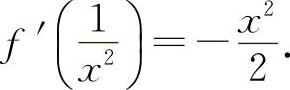 所以
所以 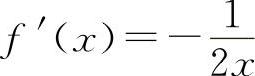 ,
,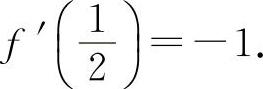
15.【分析】 函数奇偶性的证明应用其定义计算.
(1)因为 F(-x)=f(-x)-f[-(-x)]=-[f(x)-f(-x)]=-F(x)所以F(x)为奇函数.
(2)因为 F'(x)=f'(x)-f'(-x)×(-1)=f'(x)+f'(-x)而F'(-x)=f'(-x)+f'(x)=F'(x)
所以 F'(x)为偶函数.
即 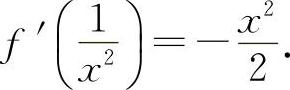 所以
所以 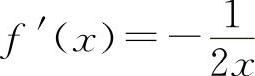 ,
,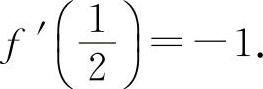
15.【分析】 函数奇偶性的证明应用其定义计算.
(1)因为 F(-x)=f(-x)-f[-(-x)]=-[f(x)-f(-x)]=-F(x)所以F(x)为奇函数.
(2)因为 F'(x)=f'(x)-f'(-x)×(-1)=f'(x)+f'(-x)而F'(-x)=f'(-x)+f'(x)=F'(x)
所以 F'(x)为偶函数.
即 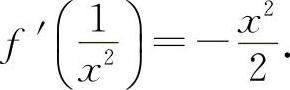 所以
所以 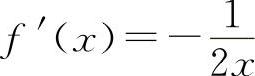 ,
,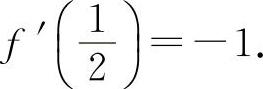
15.【分析】 函数奇偶性的证明应用其定义计算.
(1)因为 F(-x)=f(-x)-f[-(-x)]=-[f(x)-f(-x)]=-F(x)所以F(x)为奇函数.
(2)因为 F'(x)=f'(x)-f'(-x)×(-1)=f'(x)+f'(-x)而F'(-x)=f'(-x)+f'(x)=F'(x)
所以 F'(x)为偶函数.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




