1.下列函数中,在x=0处不可导的是( ).
A.y=sinx B.y=cosx C.y=ln2 D.y=|x|
2.下列函数中,在x=0处可导的是( ).
A.y=lnx B.y=|cosx| C.y=|sinx| D.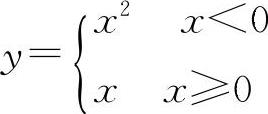
A.y=lnx B.y=|cosx| C.y=|sinx| D.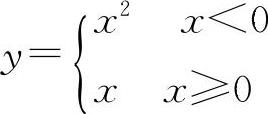
A.y=lnx B.y=|cosx| C.y=|sinx| D.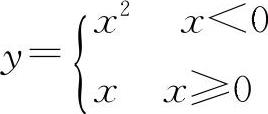
3.若函数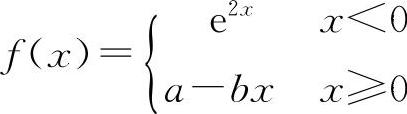 在x=0处可导,则a、b的值必为( ).
在x=0处可导,则a、b的值必为( ).
A.a=b=-1 B.a=-1,b=2 C.a=1,b=-2 D.a=b=2
4.下列各题中均假定f'(x0)存在,按照导数定义,求出下列各题中的A值.
3.若函数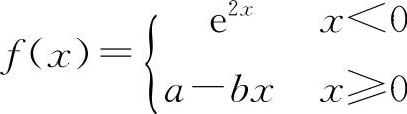 在x=0处可导,则a、b的值必为( ).
在x=0处可导,则a、b的值必为( ).
A.a=b=-1 B.a=-1,b=2 C.a=1,b=-2 D.a=b=2
4.下列各题中均假定f'(x0)存在,按照导数定义,求出下列各题中的A值.
3.若函数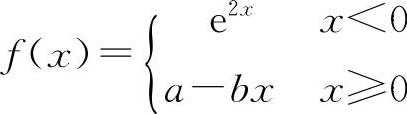 在x=0处可导,则a、b的值必为( ).
在x=0处可导,则a、b的值必为( ).
A.a=b=-1 B.a=-1,b=2 C.a=1,b=-2 D.a=b=2
4.下列各题中均假定f'(x0)存在,按照导数定义,求出下列各题中的A值.
5.设函数f(x)在x=1处可导,且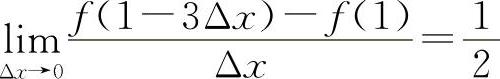 ,则f'(1)=( ).
,则f'(1)=( ).
5.设函数f(x)在x=1处可导,且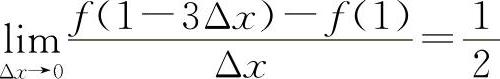 ,则f'(1)=( ).
,则f'(1)=( ).
5.设函数f(x)在x=1处可导,且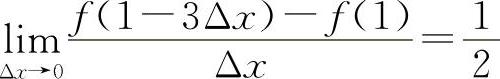 ,则f'(1)=( ).
,则f'(1)=( ).
6.曲线y=x+ex在x=0处的切线方程是( ).
A.2x-y+1=0 B.2x-y+2=0
C.x-y+1=0 D.x-y+2=0
7.过曲线y=2x2-x-2上的一点M作切线,如果切线与直线y=4x-1平行,则切点坐标为____.
8.求下列函数的一阶导数.
6.曲线y=x+ex在x=0处的切线方程是( ).
A.2x-y+1=0 B.2x-y+2=0
C.x-y+1=0 D.x-y+2=0
7.过曲线y=2x2-x-2上的一点M作切线,如果切线与直线y=4x-1平行,则切点坐标为____.
8.求下列函数的一阶导数.
6.曲线y=x+ex在x=0处的切线方程是( ).
A.2x-y+1=0 B.2x-y+2=0
C.x-y+1=0 D.x-y+2=0
7.过曲线y=2x2-x-2上的一点M作切线,如果切线与直线y=4x-1平行,则切点坐标为____.
8.求下列函数的一阶导数.
9.用对数求导法求下列函数的一阶导数.
9.用对数求导法求下列函数的一阶导数.
9.用对数求导法求下列函数的一阶导数.
10.求下列隐函数的一阶导数y'.
(1)ysinx-cos(x-y)=0 (2)y=tan(x+y)
(3)x2+y2=1+exy(4)ex+y+cos(xy)=0
11.求下列函数的二阶导数.
(1)y=x3 lnx (2)y=cos2x·lnx
12.求下列函数的微分.
10.求下列隐函数的一阶导数y'.
(1)ysinx-cos(x-y)=0 (2)y=tan(x+y)
(3)x2+y2=1+exy(4)ex+y+cos(xy)=0
11.求下列函数的二阶导数.
(1)y=x3 lnx (2)y=cos2x·lnx(https://www.xing528.com)
12.求下列函数的微分.
10.求下列隐函数的一阶导数y'.
(1)ysinx-cos(x-y)=0 (2)y=tan(x+y)
(3)x2+y2=1+exy(4)ex+y+cos(xy)=0
11.求下列函数的二阶导数.
(1)y=x3 lnx (2)y=cos2x·lnx
12.求下列函数的微分.
(1)y=tan2(1+2x2) (2)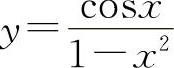
13.将适当的函数填入下列括号内,使等式成立(可以不加任意常数C).
(1)d( )=2dx (2)d( )=3xdx
(3)d( )=costdt (4)d( )=sin3xdx
(1)y=tan2(1+2x2) (2)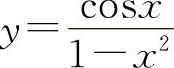
13.将适当的函数填入下列括号内,使等式成立(可以不加任意常数C).
(1)d( )=2dx (2)d( )=3xdx
(3)d( )=costdt (4)d( )=sin3xdx
(1)y=tan2(1+2x2) (2)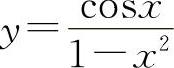
13.将适当的函数填入下列括号内,使等式成立(可以不加任意常数C).
(1)d( )=2dx (2)d( )=3xdx
(3)d( )=costdt (4)d( )=sin3xdx
(5)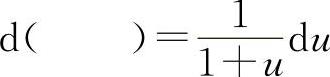
(5)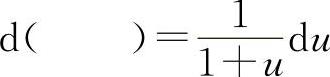
(5)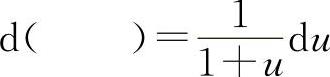
(6)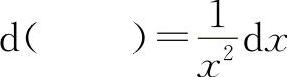
(6)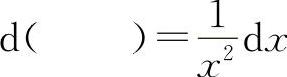
(6)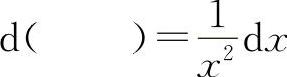
(7)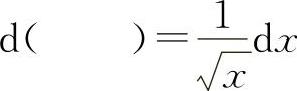
(7)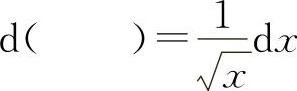
(7)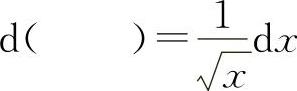
(8)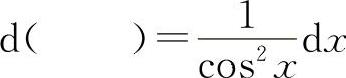
(8)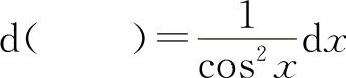
(8)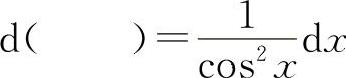
(9)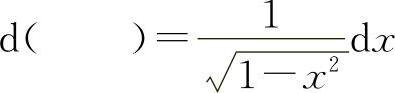
(9)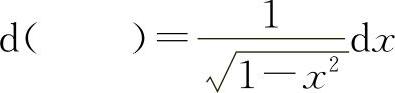
(9)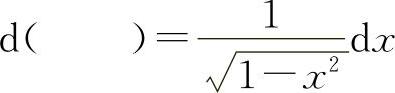
(10)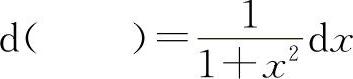
(10)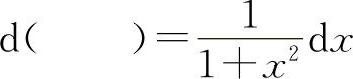
(10)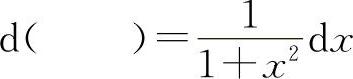
14.若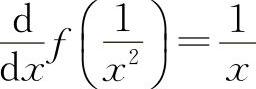 ,求f'(x)及
,求f'(x)及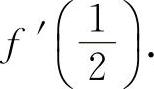
15.设函数F(x)=f(x)-f(-x),且f(x)可导,
证明(1)F(x)为奇函数,(2)F'(x)为偶函数.
14.若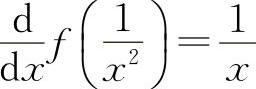 ,求f'(x)及
,求f'(x)及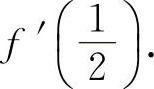
15.设函数F(x)=f(x)-f(-x),且f(x)可导,
证明(1)F(x)为奇函数,(2)F'(x)为偶函数.
14.若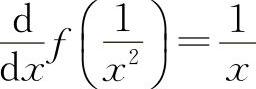 ,求f'(x)及
,求f'(x)及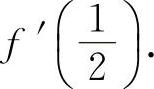
15.设函数F(x)=f(x)-f(-x),且f(x)可导,
证明(1)F(x)为奇函数,(2)F'(x)为偶函数.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




