1.无穷小量概念及无穷小量的比较.共考8次,考到的概率为40%.此书仅选择了近几年的试题,其他的试题可查看本社出版的“专升本考点汇编与试题精解”.
(1)(0202)当x→0时,ln(1+x)与x比较是( ).
A.高阶的无穷小 B.等价的无穷小
C.非等价的同阶无穷小 D.低阶的无穷小
(2)(0408) 当x→0时,函数f(x)与sinx是等价无穷小,则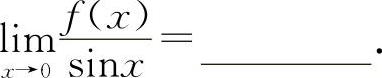
(2)(0408) 当x→0时,函数f(x)与sinx是等价无穷小,则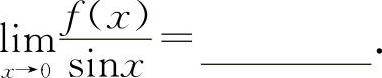
(2)(0408) 当x→0时,函数f(x)与sinx是等价无穷小,则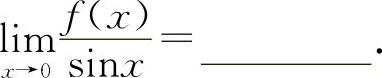
(3)(1012) 当x→0时,f(x)与sin2x是等价无穷小,则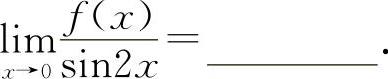
【分析】 无穷小量的判定应根据定义.而无穷小量的比较是求它们比的极限.
(3)(1012) 当x→0时,f(x)与sin2x是等价无穷小,则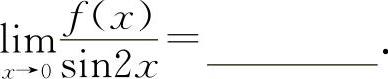
【分析】 无穷小量的判定应根据定义.而无穷小量的比较是求它们比的极限.
(3)(1012) 当x→0时,f(x)与sin2x是等价无穷小,则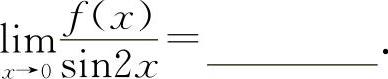
【分析】 无穷小量的判定应根据定义.而无穷小量的比较是求它们比的极限.
(1)选B选项.因为 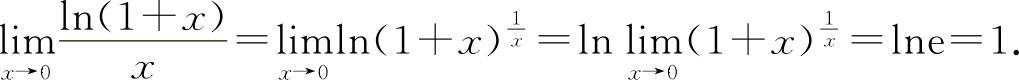
(2)填1. 根据等价无穷小的定义.
(3)填1. 根据等价无穷小的定义.
(1)选B选项.因为 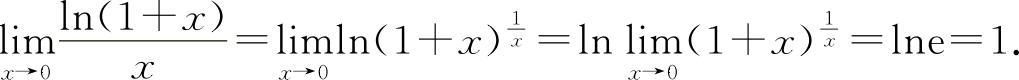
(2)填1. 根据等价无穷小的定义.
(3)填1. 根据等价无穷小的定义.
(1)选B选项.因为 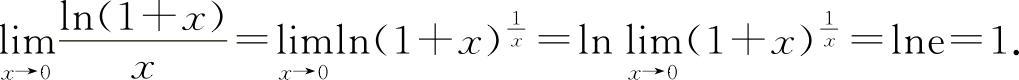
(2)填1. 根据等价无穷小的定义.
(3)填1. 根据等价无穷小的定义.
2.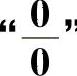 ”型不定式极限.共考20次,此类型题为必考题.
”型不定式极限.共考20次,此类型题为必考题.
2.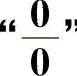 ”型不定式极限.共考20次,此类型题为必考题.
”型不定式极限.共考20次,此类型题为必考题.
2.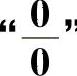 ”型不定式极限.共考20次,此类型题为必考题.
”型不定式极限.共考20次,此类型题为必考题.
(1)(0621) 求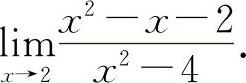
(1)(0621) 求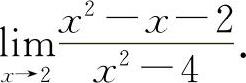
(1)(0621) 求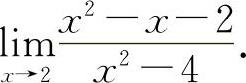
(2)(0721) 求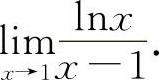
(2)(0721) 求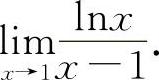
(2)(0721) 求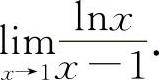
(3)(0821) 求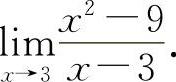
(3)(0821) 求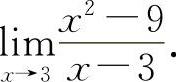
(3)(0821) 求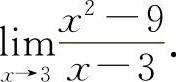
(4)(0921) 求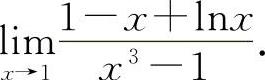
(4)(0921) 求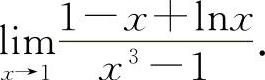
(4)(0921) 求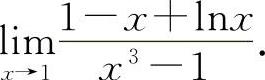
(5)(1021) 求
(5)(1021) 求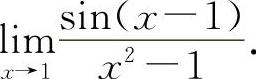
(5)(1021) 求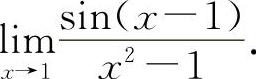
(6)(1101)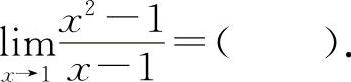
A.0 B.1 C.2 D.3
(6)(1101)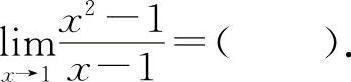
A.0 B.1 C.2 D.3
(6)(1101)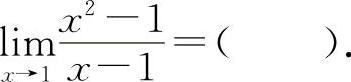
A.0 B.1 C.2 D.3
(7)(1221)计算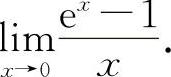
(7)(1221)计算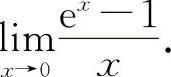
(7)(1221)计算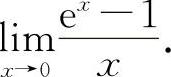
(8)(1321)计算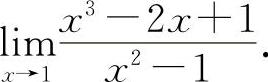
(8)(1321)计算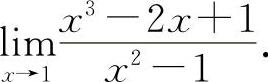
(8)(1321)计算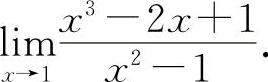
【分析】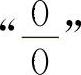 型不定式极限的求法是每年专升本试题中必考的内容之一,考生必须熟练掌握.
型不定式极限的求法是每年专升本试题中必考的内容之一,考生必须熟练掌握.
【分析】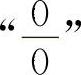 型不定式极限的求法是每年专升本试题中必考的内容之一,考生必须熟练掌握.
型不定式极限的求法是每年专升本试题中必考的内容之一,考生必须熟练掌握.
【分析】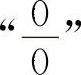 型不定式极限的求法是每年专升本试题中必考的内容之一,考生必须熟练掌握.
型不定式极限的求法是每年专升本试题中必考的内容之一,考生必须熟练掌握.
求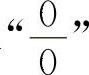 型不定式极限的常用方法是利用等价无穷小量代换以及洛必达法则求解(对于极限式中有根式的,首先有理化,再进行计算较简捷).
型不定式极限的常用方法是利用等价无穷小量代换以及洛必达法则求解(对于极限式中有根式的,首先有理化,再进行计算较简捷).
常用的等价无穷小量代换有:
当x→0时sinx~x;tanx~x;ln(1+x)~x;arcsinx~x;arctanx~x;ex-1~x.
其结构为当▭→0时,sin▭~▭;ln(1+▭)~▭.
其余类同.式中的“▭”既可以是x也可以是x的函数,只要当x→x0时,有“▭”→0即可用上面的结构式.
例如,当x→0时,sin(x2-x)~x2-x,▭=x2-x→0.
当x→1时,ln(x2)=ln(1+x2-1)~x2-1.
而当x→0时,ln(1-2x2)~(-2x2).
求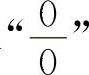 型不定式极限的常用方法是利用等价无穷小量代换以及洛必达法则求解(对于极限式中有根式的,首先有理化,再进行计算较简捷).
型不定式极限的常用方法是利用等价无穷小量代换以及洛必达法则求解(对于极限式中有根式的,首先有理化,再进行计算较简捷).
常用的等价无穷小量代换有:
当x→0时sinx~x;tanx~x;ln(1+x)~x;arcsinx~x;arctanx~x;ex-1~x.
其结构为当▭→0时,sin▭~▭;ln(1+▭)~▭.
其余类同.式中的“▭”既可以是x也可以是x的函数,只要当x→x0时,有“▭”→0即可用上面的结构式.
例如,当x→0时,sin(x2-x)~x2-x,▭=x2-x→0.
当x→1时,ln(x2)=ln(1+x2-1)~x2-1.
而当x→0时,ln(1-2x2)~(-2x2).
求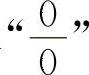 型不定式极限的常用方法是利用等价无穷小量代换以及洛必达法则求解(对于极限式中有根式的,首先有理化,再进行计算较简捷).
型不定式极限的常用方法是利用等价无穷小量代换以及洛必达法则求解(对于极限式中有根式的,首先有理化,再进行计算较简捷).
常用的等价无穷小量代换有:
当x→0时sinx~x;tanx~x;ln(1+x)~x;arcsinx~x;arctanx~x;ex-1~x.
其结构为当▭→0时,sin▭~▭;ln(1+▭)~▭.
其余类同.式中的“▭”既可以是x也可以是x的函数,只要当x→x0时,有“▭”→0即可用上面的结构式.
例如,当x→0时,sin(x2-x)~x2-x,▭=x2-x→0.
当x→1时,ln(x2)=ln(1+x2-1)~x2-1.
而当x→0时,ln(1-2x2)~(-2x2).
3.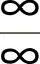 型不定式极限.共考5次,考到的概率为25%.(1)(0701)
型不定式极限.共考5次,考到的概率为25%.(1)(0701) 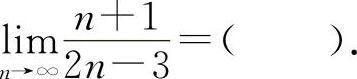
3.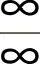 型不定式极限.共考5次,考到的概率为25%.(1)(0701)
型不定式极限.共考5次,考到的概率为25%.(1)(0701) 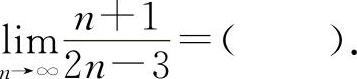
3.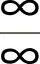 型不定式极限.共考5次,考到的概率为25%.(1)(0701)
型不定式极限.共考5次,考到的概率为25%.(1)(0701) 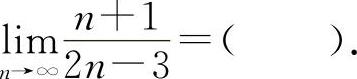
A.0 B.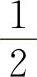
C.1 D.2
A.0 B.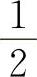
C.1 D.2
A.0 B.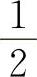
C.1 D.2
(2)(0801) 
(2)(0801) 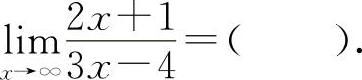
(2)(0801) 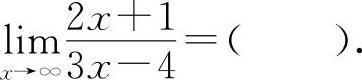
A.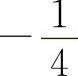 B.0 C.
B.0 C.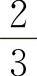 D.1
D.1
A.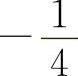 B.0 C.
B.0 C.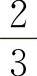 D.1
D.1
A.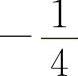 B.0 C.
B.0 C.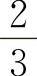 D.1
D.1
(3)(1011) 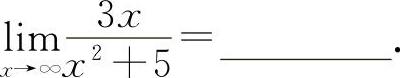
(3)(1011) 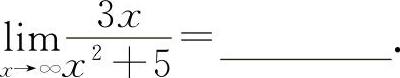
(3)(1011) 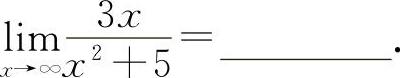
【分析】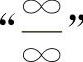 型不定式极限的计算,常用的办法是消去分子与分母中最高阶无穷因子.
型不定式极限的计算,常用的办法是消去分子与分母中最高阶无穷因子.
则有e3a=27,3a=ln27=3ln3,所以a=ln3【分析】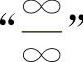 型不定式极限的计算,常用的办法是消去分子与分母中最高阶无穷因子.(https://www.xing528.com)
型不定式极限的计算,常用的办法是消去分子与分母中最高阶无穷因子.(https://www.xing528.com)
(1)选B选项.因为 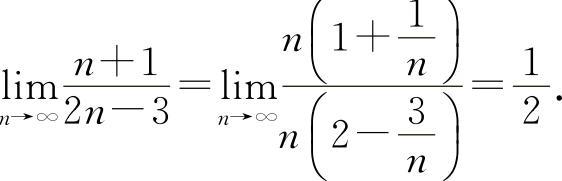
(1)选B选项.因为 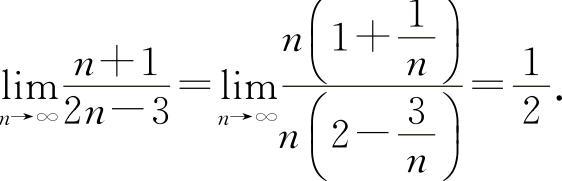
(1)选B选项.因为 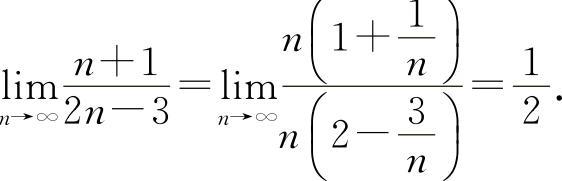
(2)选C选项.因为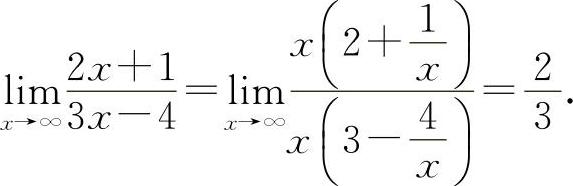
(2)选C选项.因为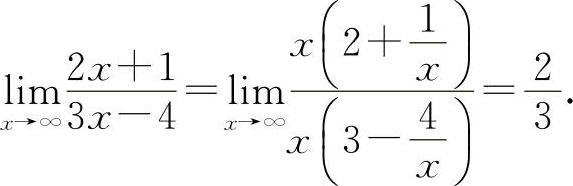
(2)选C选项.因为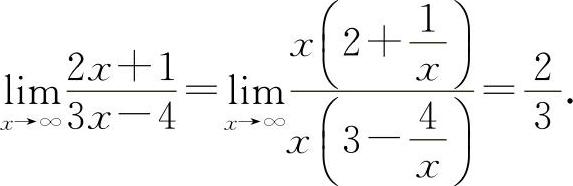
(3)填0.因为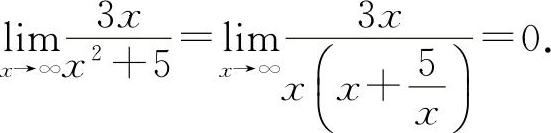
4.重要极限Ⅰ.共考11次,考到的概率为55%.
(3)填0.因为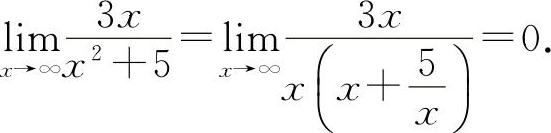
4.重要极限Ⅰ.共考11次,考到的概率为55%.
(3)填0.因为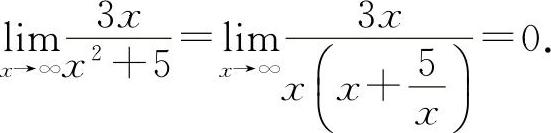
4.重要极限Ⅰ.共考11次,考到的概率为55%.
【分析】 重要极限Ⅰ 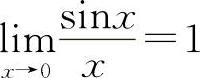 的结构式是
的结构式是 
【分析】 重要极限Ⅰ 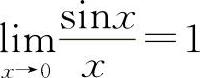 的结构式是
的结构式是 
【分析】 重要极限Ⅰ 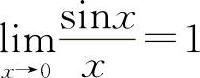 的结构式是
的结构式是 
式中的方块“▭”既可以是x,又可以是x的函数,而▭→0是表示当x→x0(或∞)时必有▭→0,只有符合上述结构式的极限才是1.例如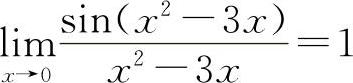 ,而
,而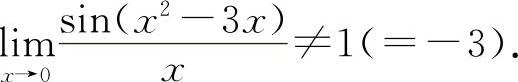
式中的方块“▭”既可以是x,又可以是x的函数,而▭→0是表示当x→x0(或∞)时必有▭→0,只有符合上述结构式的极限才是1.例如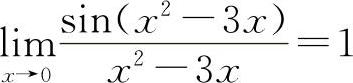 ,而
,而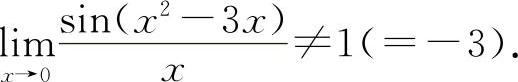
式中的方块“▭”既可以是x,又可以是x的函数,而▭→0是表示当x→x0(或∞)时必有▭→0,只有符合上述结构式的极限才是1.例如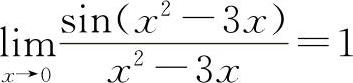 ,而
,而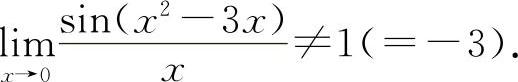
(1)填3.因为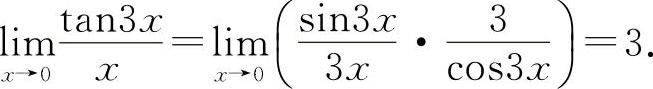
(1)填3.因为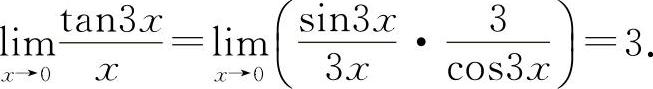
(1)填3.因为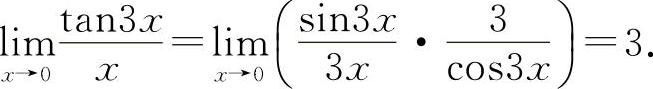
(2)填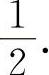 因为
因为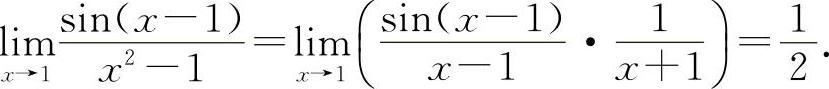
(2)填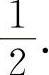 因为
因为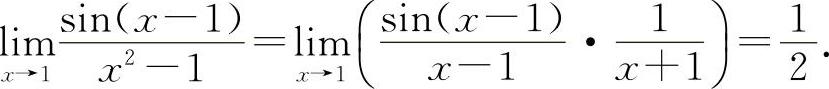
(2)填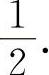 因为
因为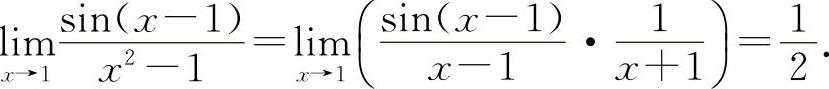
(3)填2.因为
(4)填1.根据重要极限Ⅰ的结构式得解.
(3)填2.因为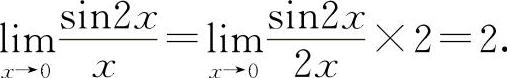
(4)填1.根据重要极限Ⅰ的结构式得解.
(3)填2.因为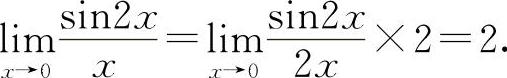
(4)填1.根据重要极限Ⅰ的结构式得解.
(5)填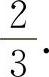 因为
因为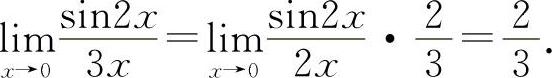
5.重要极限Ⅱ.共考13次,考到的概率为65%.
(5)填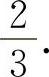 因为
因为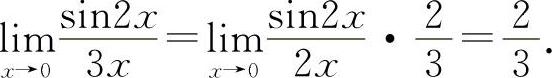
5.重要极限Ⅱ.共考13次,考到的概率为65%.
(5)填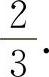 因为
因为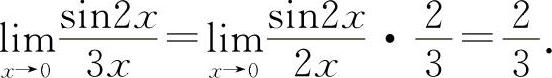
5.重要极限Ⅱ.共考13次,考到的概率为65%.
(1)(0601) 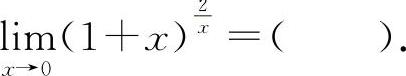
A.1 B.e C.2e D.e2
(1)(0601) 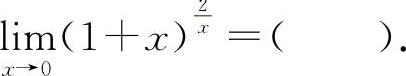
A.1 B.e C.2e D.e2
(1)(0601) 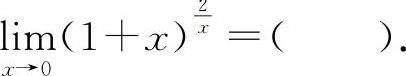
A.1 B.e C.2e D.e2
(2)(0912) 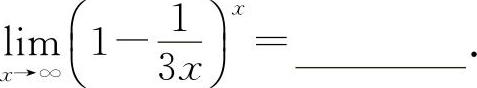
(2)(0912) 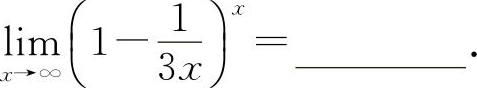
(2)(0912) 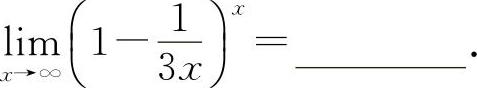
(3)(1121)计算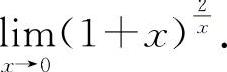
(3)(1121)计算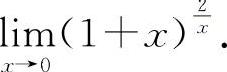
(3)(1121)计算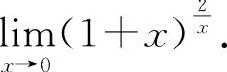
(4)(1315) 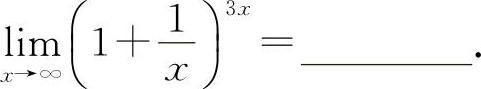
(4)(1315) 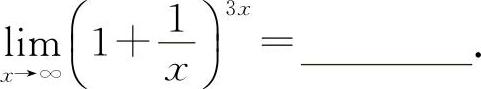
(4)(1315) 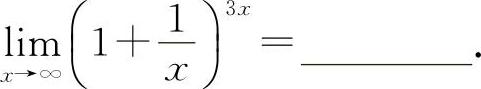
【分析】重要极限Ⅱ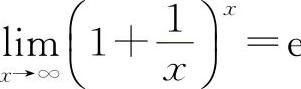 ;
;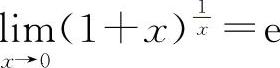 或
或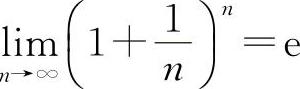 的结构式是
的结构式是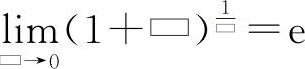 ,式中的方块“▭”与重要极限Ⅰ中的意义相同.
,式中的方块“▭”与重要极限Ⅰ中的意义相同.
【分析】重要极限Ⅱ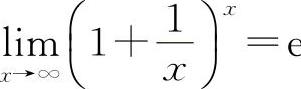 ;
;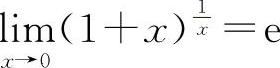 或
或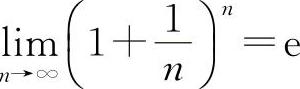 的结构式是
的结构式是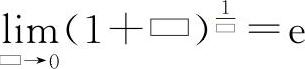 ,式中的方块“▭”与重要极限Ⅰ中的意义相同.
,式中的方块“▭”与重要极限Ⅰ中的意义相同.
【分析】重要极限Ⅱ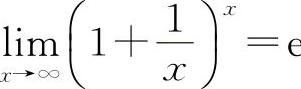 ;
;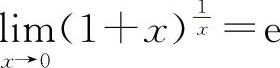 或
或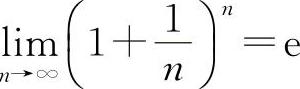 的结构式是
的结构式是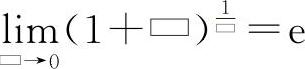 ,式中的方块“▭”与重要极限Ⅰ中的意义相同.
,式中的方块“▭”与重要极限Ⅰ中的意义相同.
(1)选D选项.因为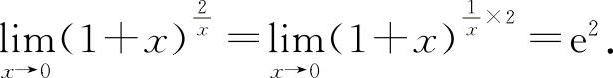
(1)选D选项.因为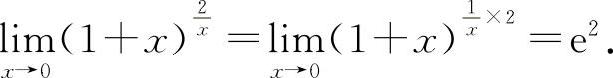
(1)选D选项.因为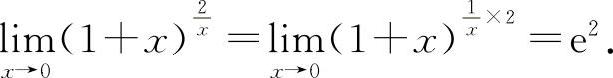
(2)填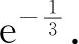 因为
因为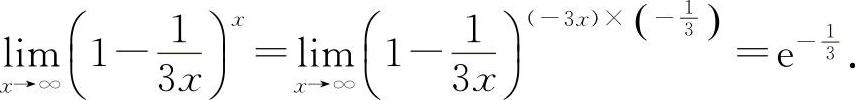
(2)填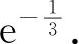 因为
因为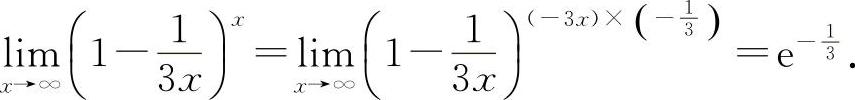
(2)填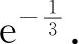 因为
因为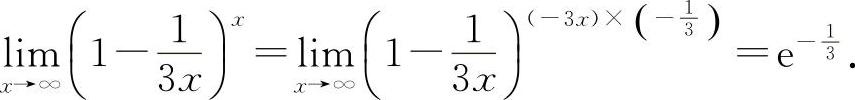
(4)填e3.
6.连续性.共考12次,考到的概率为60%.
(4)填e3.
6.连续性.共考12次,考到的概率为60%.
(4)填e3.
6.连续性.共考12次,考到的概率为60%.
(1)(0209)设函数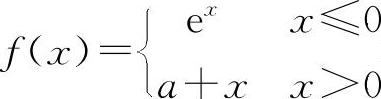 在点x=0处连续,则常数a=____.
在点x=0处连续,则常数a=____.
(1)(0209)设函数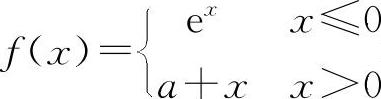 在点x=0处连续,则常数a=____.
在点x=0处连续,则常数a=____.
(1)(0209)设函数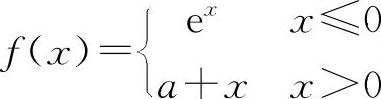 在点x=0处连续,则常数a=____.
在点x=0处连续,则常数a=____.
(2)(0613)设函数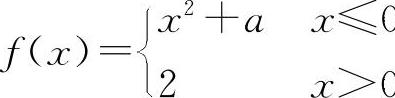 在x=0处连续,则a=____.
在x=0处连续,则a=____.
(2)(0613)设函数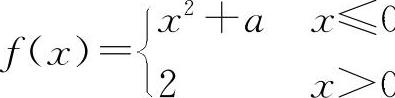 在x=0处连续,则a=____.
在x=0处连续,则a=____.
(2)(0613)设函数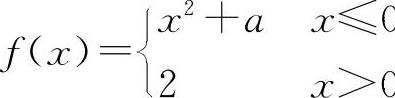 在x=0处连续,则a=____.
在x=0处连续,则a=____.
(3)(1013)设函数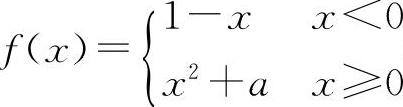 在点x=0处的极限存在,则a=____.
在点x=0处的极限存在,则a=____.
(3)(1013)设函数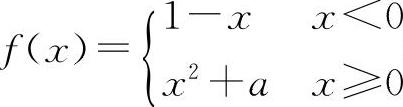 在点x=0处的极限存在,则a=____.
在点x=0处的极限存在,则a=____.
(3)(1013)设函数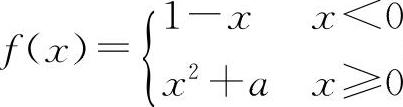 在点x=0处的极限存在,则a=____.
在点x=0处的极限存在,则a=____.
(4)(1213)设函数 在x=0处连续,则a=____.
在x=0处连续,则a=____.
(4)(1213)设函数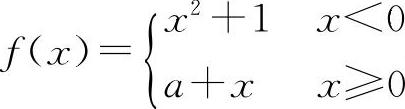 在x=0处连续,则a=____.
在x=0处连续,则a=____.
(4)(1213)设函数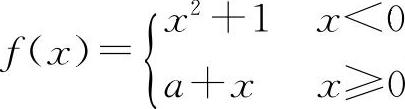 在x=0处连续,则a=____.
在x=0处连续,则a=____.
(5)(1312)设函数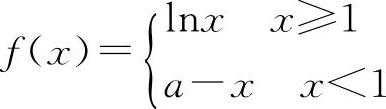 在x=1处连续,则a=____.
在x=1处连续,则a=____.
【分析】分段函数在分段点处的连续性只需计算左、右极限并使其等于函数值即可.即使f(x0-0)=f(x0+0)=f(x0),就可确定在x0处的连续条件.若上述等式不成立,则该点为间断点.
(1)填1. 因为f(0-0)=1,而f(0+0)=a,所以a=1.
(2)填2. 因为f(0-0)=f(0)=a,f(0+0)=2,所以a=2.
(3)填1. 因为f(0-0)=1,f(0+0)=a,所以a=1.
(4)填1. 同(3).
(5)填1. 同(3).
(5)(1312)设函数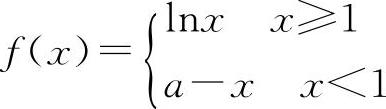 在x=1处连续,则a=____.
在x=1处连续,则a=____.
【分析】分段函数在分段点处的连续性只需计算左、右极限并使其等于函数值即可.即使f(x0-0)=f(x0+0)=f(x0),就可确定在x0处的连续条件.若上述等式不成立,则该点为间断点.
(1)填1. 因为f(0-0)=1,而f(0+0)=a,所以a=1.
(2)填2. 因为f(0-0)=f(0)=a,f(0+0)=2,所以a=2.
(3)填1. 因为f(0-0)=1,f(0+0)=a,所以a=1.
(4)填1. 同(3).
(5)填1. 同(3).
(5)(1312)设函数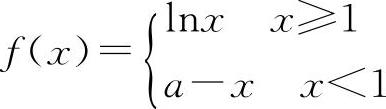 在x=1处连续,则a=____.
在x=1处连续,则a=____.
【分析】分段函数在分段点处的连续性只需计算左、右极限并使其等于函数值即可.即使f(x0-0)=f(x0+0)=f(x0),就可确定在x0处的连续条件.若上述等式不成立,则该点为间断点.
(1)填1. 因为f(0-0)=1,而f(0+0)=a,所以a=1.
(2)填2. 因为f(0-0)=f(0)=a,f(0+0)=2,所以a=2.
(3)填1. 因为f(0-0)=1,f(0+0)=a,所以a=1.
(4)填1. 同(3).
(5)填1. 同(3).
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




