1.求极限
求函数极限的常用方法主要有:
(1)利用极限的四则运算法则.
(2)利用函数的连续性:若f(x)在x0处连续,则
(2)利用函数的连续性:若f(x)在x0处连续,则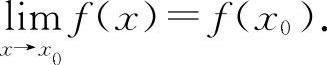
(2)利用函数的连续性:若f(x)在x0处连续,则
(3)对于 型不定式,可考虑用因式分解消去零因子法;用等价无穷小量代换法以及重要极限
型不定式,可考虑用因式分解消去零因子法;用等价无穷小量代换法以及重要极限 等方法.
等方法.
(3)对于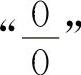 型不定式,可考虑用因式分解消去零因子法;用等价无穷小量代换法以及重要极限
型不定式,可考虑用因式分解消去零因子法;用等价无穷小量代换法以及重要极限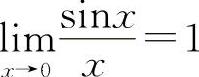 等方法.
等方法.
(3)对于 型不定式,可考虑用因式分解消去零因子法;用等价无穷小量代换法以及重要极限
型不定式,可考虑用因式分解消去零因子法;用等价无穷小量代换法以及重要极限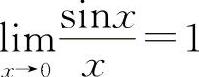 等方法.
等方法.
(4)对于 型不定式,可考虑消去无穷因子法.对于
型不定式,可考虑消去无穷因子法.对于 型与
型与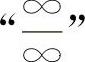 型的不定式,在第二章中还将介绍洛必达法则.
型的不定式,在第二章中还将介绍洛必达法则.
(4)对于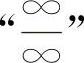 型不定式,可考虑消去无穷因子法.对于
型不定式,可考虑消去无穷因子法.对于 型与
型与 型的不定式,在第二章中还将介绍洛必达法则.
型的不定式,在第二章中还将介绍洛必达法则.
(4)对于 型不定式,可考虑消去无穷因子法.对于
型不定式,可考虑消去无穷因子法.对于 型与
型与 型的不定式,在第二章中还将介绍洛必达法则.
型的不定式,在第二章中还将介绍洛必达法则.
(5)对于“∞-∞”型与“0·∞”型的不定式,应先化为 型或
型或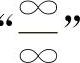 型,再用上述方法求解.
型,再用上述方法求解.
(6)利用两个重要极限
(5)对于“∞-∞”型与“0·∞”型的不定式,应先化为 型或
型或 型,再用上述方法求解.
型,再用上述方法求解.
(6)利用两个重要极限
(5)对于“∞-∞”型与“0·∞”型的不定式,应先化为 型或
型或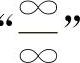 型,再用上述方法求解.
型,再用上述方法求解.
(6)利用两个重要极限
注意两个重要极限的结构式分别为
注意两个重要极限的结构式分别为
注意两个重要极限的结构式分别为
其中方块“▭”内可以为x,也可以为x的函数,只要满足上述结构形式,公式都正确.
(7)利用无穷小量的性质.主要是“无穷小量与有界变量之积为无穷小量”以及“无穷大量的倒数为无穷小量”.(https://www.xing528.com)
(8)利用等价无穷小量代换.利用等价无穷小量代换常能简化运算,但是等价无穷小量代换能在乘除法中使用,限于知识面的原因不要在加减法中使用.常用的等价无穷小量代换有:
其中方块“▭”内可以为x,也可以为x的函数,只要满足上述结构形式,公式都正确.
(7)利用无穷小量的性质.主要是“无穷小量与有界变量之积为无穷小量”以及“无穷大量的倒数为无穷小量”.
(8)利用等价无穷小量代换.利用等价无穷小量代换常能简化运算,但是等价无穷小量代换能在乘除法中使用,限于知识面的原因不要在加减法中使用.常用的等价无穷小量代换有:
其中方块“▭”内可以为x,也可以为x的函数,只要满足上述结构形式,公式都正确.
(7)利用无穷小量的性质.主要是“无穷小量与有界变量之积为无穷小量”以及“无穷大量的倒数为无穷小量”.
(8)利用等价无穷小量代换.利用等价无穷小量代换常能简化运算,但是等价无穷小量代换能在乘除法中使用,限于知识面的原因不要在加减法中使用.常用的等价无穷小量代换有:
当x→0时,sinx~x;tanx~x;arcsinx~x;arctanx~x;ln(1+x)~x; 上述各式也应该理解为:当x→x0(∞)时,▭→0,则有
上述各式也应该理解为:当x→x0(∞)时,▭→0,则有
sin▭~▭;tan▭~▭等.
其中▭内可以为x,也可以为x的函数.
(9)求分段函数在分段点处的极限时,一定要分别求左极限与右极限,然后再判定极限是否存在.
2.判定函数的连续性,利用闭区间上连续函数的“零点定理”推证方程的根的存在性.
当x→0时,sinx~x;tanx~x;arcsinx~x;arctanx~x;ln(1+x)~x; 上述各式也应该理解为:当x→x0(∞)时,▭→0,则有
上述各式也应该理解为:当x→x0(∞)时,▭→0,则有
sin▭~▭;tan▭~▭等.
其中▭内可以为x,也可以为x的函数.
(9)求分段函数在分段点处的极限时,一定要分别求左极限与右极限,然后再判定极限是否存在.
2.判定函数的连续性,利用闭区间上连续函数的“零点定理”推证方程的根的存在性.
当x→0时,sinx~x;tanx~x;arcsinx~x;arctanx~x;ln(1+x)~x; 上述各式也应该理解为:当x→x0(∞)时,▭→0,则有
上述各式也应该理解为:当x→x0(∞)时,▭→0,则有
sin▭~▭;tan▭~▭等.
其中▭内可以为x,也可以为x的函数.
(9)求分段函数在分段点处的极限时,一定要分别求左极限与右极限,然后再判定极限是否存在.
2.判定函数的连续性,利用闭区间上连续函数的“零点定理”推证方程的根的存在性.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




