1.选A选项【分析】由连续的定义: ,但
,但 极限值A不一定等于该点的函数值f(x0),所以应选A选项.
极限值A不一定等于该点的函数值f(x0),所以应选A选项.
2.选A选项【分析】由于函数在一点连续是要求极限值等于函数值,所以极限中的一些结论可用到连续上来.
对于A选项可以反证法.若f(x)+g(x)在点x0处连续,则必有g(x)=[f(x)+g(x)]-f(x)在点x0处必连续,与已知矛盾,所以应选A选项.对于B、C、D选项,只需举出反例即可.
1.选A选项【分析】由连续的定义: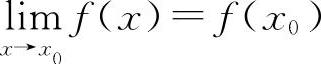 ,但
,但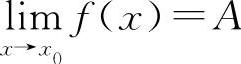 极限值A不一定等于该点的函数值f(x0),所以应选A选项.
极限值A不一定等于该点的函数值f(x0),所以应选A选项.
2.选A选项【分析】由于函数在一点连续是要求极限值等于函数值,所以极限中的一些结论可用到连续上来.
对于A选项可以反证法.若f(x)+g(x)在点x0处连续,则必有g(x)=[f(x)+g(x)]-f(x)在点x0处必连续,与已知矛盾,所以应选A选项.对于B、C、D选项,只需举出反例即可.
1.选A选项【分析】由连续的定义: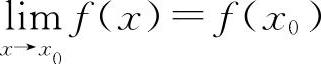 ,但
,但 极限值A不一定等于该点的函数值f(x0),所以应选A选项.
极限值A不一定等于该点的函数值f(x0),所以应选A选项.
2.选A选项【分析】由于函数在一点连续是要求极限值等于函数值,所以极限中的一些结论可用到连续上来.
对于A选项可以反证法.若f(x)+g(x)在点x0处连续,则必有g(x)=[f(x)+g(x)]-f(x)在点x0处必连续,与已知矛盾,所以应选A选项.对于B、C、D选项,只需举出反例即可.
对于选项B选项,设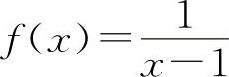 ,
, ,在x=1处,f(x)与g(x)均不连续,但f(x)+g(x)=2x在x=1处是连续的,排除B选项.
,在x=1处,f(x)与g(x)均不连续,但f(x)+g(x)=2x在x=1处是连续的,排除B选项.
对于选项B选项,设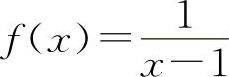 ,
,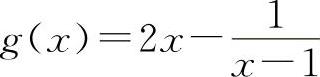 ,在x=1处,f(x)与g(x)均不连续,但f(x)+g(x)=2x在x=1处是连续的,排除B选项.
,在x=1处,f(x)与g(x)均不连续,但f(x)+g(x)=2x在x=1处是连续的,排除B选项.
对于选项B选项,设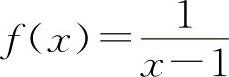 ,
,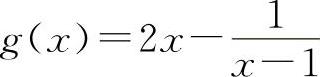 ,在x=1处,f(x)与g(x)均不连续,但f(x)+g(x)=2x在x=1处是连续的,排除B选项.
,在x=1处,f(x)与g(x)均不连续,但f(x)+g(x)=2x在x=1处是连续的,排除B选项.
对于C选项,设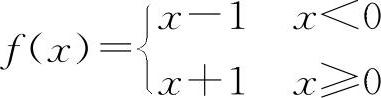 ,在x=0处f(x)不连续.但
,在x=0处f(x)不连续.但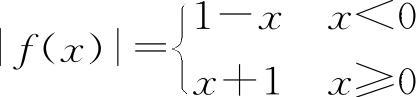 ,在x=0处|f(x)|连续,应排除C选项.
,在x=0处|f(x)|连续,应排除C选项.
对于C选项,设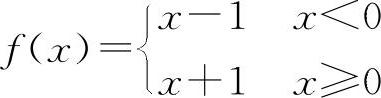 ,在x=0处f(x)不连续.但
,在x=0处f(x)不连续.但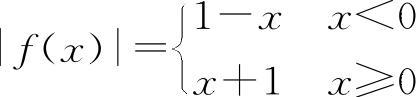 ,在x=0处|f(x)|连续,应排除C选项.
,在x=0处|f(x)|连续,应排除C选项.
对于C选项,设 ,在x=0处f(x)不连续.但
,在x=0处f(x)不连续.但 ,在x=0处|f(x)|连续,应排除C选项.
,在x=0处|f(x)|连续,应排除C选项.
对于D选项,设 ,则
,则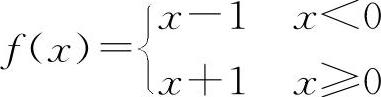 ,|f(x)|在x=0处连续,而f(x)在x=0处不连续,应排除D选项.
,|f(x)|在x=0处连续,而f(x)在x=0处不连续,应排除D选项.
3.选B选项【分析】由连续的三要素可知B选项正确,所以应选B选项.
4.选D选项【分析】只需计算f(0-0),f(0+0),且使f(0-0)=f(0+0)=f(0)即可确定p和q的值.
对于D选项,设 ,则
,则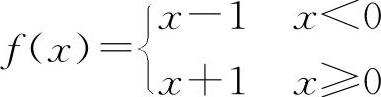 ,|f(x)|在x=0处连续,而f(x)在x=0处不连续,应排除D选项.
,|f(x)|在x=0处连续,而f(x)在x=0处不连续,应排除D选项.
3.选B选项【分析】由连续的三要素可知B选项正确,所以应选B选项.(https://www.xing528.com)
4.选D选项【分析】只需计算f(0-0),f(0+0),且使f(0-0)=f(0+0)=f(0)即可确定p和q的值.
对于D选项,设 ,则
,则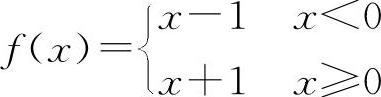 ,|f(x)|在x=0处连续,而f(x)在x=0处不连续,应排除D选项.
,|f(x)|在x=0处连续,而f(x)在x=0处不连续,应排除D选项.
3.选B选项【分析】由连续的三要素可知B选项正确,所以应选B选项.
4.选D选项【分析】只需计算f(0-0),f(0+0),且使f(0-0)=f(0+0)=f(0)即可确定p和q的值.
因为 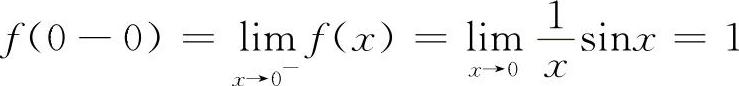

由 f(0-0)=f(0) 得p=1;f(0+0)=f(0) 得q=1
所以选D选项.
5.【分析】利用“零点定理”可得证明.
因为 
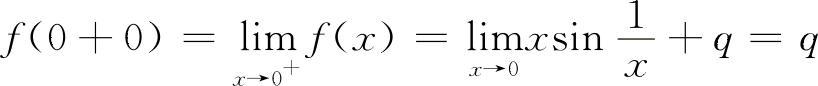
由 f(0-0)=f(0) 得p=1;f(0+0)=f(0) 得q=1
所以选D选项.
5.【分析】利用“零点定理”可得证明.
因为 
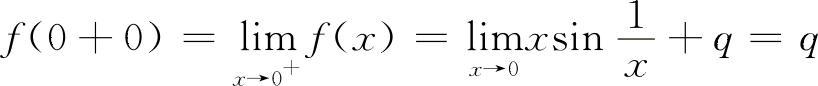
由 f(0-0)=f(0) 得p=1;f(0+0)=f(0) 得q=1
所以选D选项.
5.【分析】利用“零点定理”可得证明.
因为f(x)=4x-2x在 上连续,又f(0)=-1,
上连续,又f(0)=-1,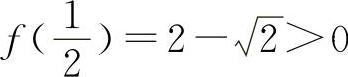 ,所以f(0)·
,所以f(0)·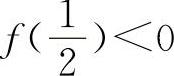 ,则必存在
,则必存在 ,使f(ξ)=0,即存在x=ξ使4ξ-2ξ=0,也即方程4x=2x至少有一个根在0与
,使f(ξ)=0,即存在x=ξ使4ξ-2ξ=0,也即方程4x=2x至少有一个根在0与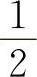 之间.
之间.
因为f(x)=4x-2x在 上连续,又f(0)=-1,
上连续,又f(0)=-1, ,所以f(0)·
,所以f(0)·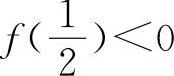 ,则必存在
,则必存在 ,使f(ξ)=0,即存在x=ξ使4ξ-2ξ=0,也即方程4x=2x至少有一个根在0与
,使f(ξ)=0,即存在x=ξ使4ξ-2ξ=0,也即方程4x=2x至少有一个根在0与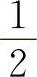 之间.
之间.
因为f(x)=4x-2x在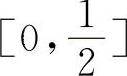 上连续,又f(0)=-1,
上连续,又f(0)=-1, ,所以f(0)·
,所以f(0)·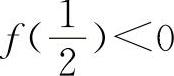 ,则必存在
,则必存在 ,使f(ξ)=0,即存在x=ξ使4ξ-2ξ=0,也即方程4x=2x至少有一个根在0与
,使f(ξ)=0,即存在x=ξ使4ξ-2ξ=0,也即方程4x=2x至少有一个根在0与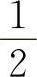 之间.
之间.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




