1.选C选项 【分析】因为函数f(x)当x→x0时的极限值与函数在该点是否有定义无关,所以应选C选项.
2.选B选项 【分析】由于数零是无穷小量,所以A选项不一定正确,根据无穷大量与无穷小量的关系可知B选项是正确的.对于C选项:当x→∞时x2sinx就是无界变量,但由于x→∞时sinx在±1之间振荡无极限,所以x2sinx当x→∞时不是无穷大量,故排除C选项,对于D选项:函数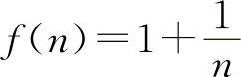 当n→∞时,它越变越小,但又不是无穷小量,排除D选项.所以选B选项.
当n→∞时,它越变越小,但又不是无穷小量,排除D选项.所以选B选项.
2.选B选项 【分析】由于数零是无穷小量,所以A选项不一定正确,根据无穷大量与无穷小量的关系可知B选项是正确的.对于C选项:当x→∞时x2sinx就是无界变量,但由于x→∞时sinx在±1之间振荡无极限,所以x2sinx当x→∞时不是无穷大量,故排除C选项,对于D选项:函数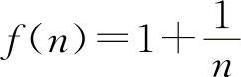 当n→∞时,它越变越小,但又不是无穷小量,排除D选项.所以选B选项.
当n→∞时,它越变越小,但又不是无穷小量,排除D选项.所以选B选项.
2.选B选项 【分析】由于数零是无穷小量,所以A选项不一定正确,根据无穷大量与无穷小量的关系可知B选项是正确的.对于C选项:当x→∞时x2sinx就是无界变量,但由于x→∞时sinx在±1之间振荡无极限,所以x2sinx当x→∞时不是无穷大量,故排除C选项,对于D选项:函数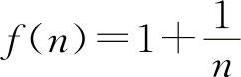 当n→∞时,它越变越小,但又不是无穷小量,排除D选项.所以选B选项.
当n→∞时,它越变越小,但又不是无穷小量,排除D选项.所以选B选项.
3.选D选项【分析】已知条件告知: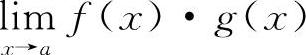 是属于∞·0的不定式极限,其极限值是不确定的,所以选D选项.
是属于∞·0的不定式极限,其极限值是不确定的,所以选D选项.
4.选A选项【分析】选项A是正确的,可用反证法来推论.如果当x→x0时f(x)+g(x)的极限存在,则[f(x)+g(x)]-f(x)=g(x)的极限存在,即g(x)的极限存在,与已知条件矛盾,所以应选A选项.因此,对于B、C、D选项,只需举例说明即可排除.
3.选D选项【分析】已知条件告知: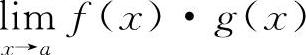 是属于∞·0的不定式极限,其极限值是不确定的,所以选D选项.
是属于∞·0的不定式极限,其极限值是不确定的,所以选D选项.
4.选A选项【分析】选项A是正确的,可用反证法来推论.如果当x→x0时f(x)+g(x)的极限存在,则[f(x)+g(x)]-f(x)=g(x)的极限存在,即g(x)的极限存在,与已知条件矛盾,所以应选A选项.因此,对于B、C、D选项,只需举例说明即可排除.
3.选D选项【分析】已知条件告知: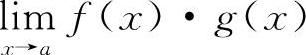 是属于∞·0的不定式极限,其极限值是不确定的,所以选D选项.
是属于∞·0的不定式极限,其极限值是不确定的,所以选D选项.
4.选A选项【分析】选项A是正确的,可用反证法来推论.如果当x→x0时f(x)+g(x)的极限存在,则[f(x)+g(x)]-f(x)=g(x)的极限存在,即g(x)的极限存在,与已知条件矛盾,所以应选A选项.因此,对于B、C、D选项,只需举例说明即可排除.
对于B选项,设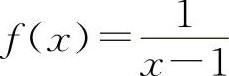 ,
,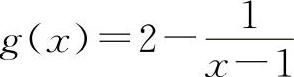 ,当x→1时f(x)与g(x)都不存在,但是其和f(x)+g(x)=2当x→1时是存在的.
,当x→1时f(x)与g(x)都不存在,但是其和f(x)+g(x)=2当x→1时是存在的.
对于B选项,设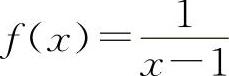 ,
,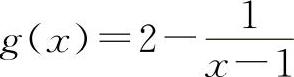 ,当x→1时f(x)与g(x)都不存在,但是其和f(x)+g(x)=2当x→1时是存在的.
,当x→1时f(x)与g(x)都不存在,但是其和f(x)+g(x)=2当x→1时是存在的.
对于B选项,设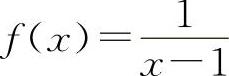 ,
,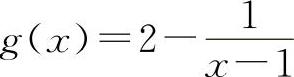 ,当x→1时f(x)与g(x)都不存在,但是其和f(x)+g(x)=2当x→1时是存在的.
,当x→1时f(x)与g(x)都不存在,但是其和f(x)+g(x)=2当x→1时是存在的.
对于C选项,设f(x)=x,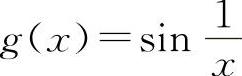 ,当x→0时,
,当x→0时,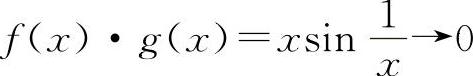 是存在的.
是存在的.
对于C选项,设f(x)=x,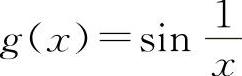 ,当x→0时,
,当x→0时,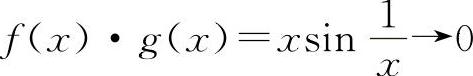 是存在的.
是存在的.
对于C选项,设f(x)=x,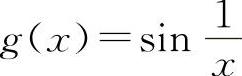 ,当x→0时,
,当x→0时,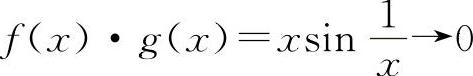 是存在的.
是存在的.
对于D选项,设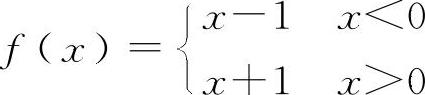 ,当x→0时f(x)不存在,但
,当x→0时f(x)不存在,但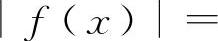
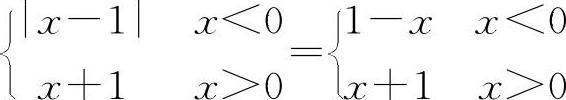 ,当x→0时|f(x)|→1是存在的.
,当x→0时|f(x)|→1是存在的.
对于D选项,设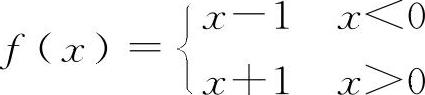 ,当x→0时f(x)不存在,但
,当x→0时f(x)不存在,但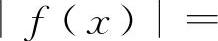
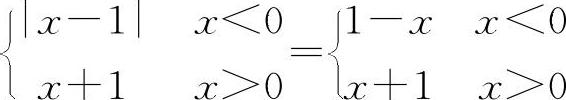 ,当x→0时|f(x)|→1是存在的.
,当x→0时|f(x)|→1是存在的.
对于D选项,设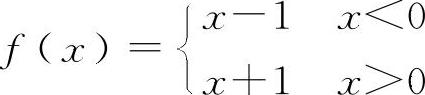 ,当x→0时f(x)不存在,但
,当x→0时f(x)不存在,但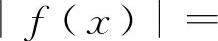
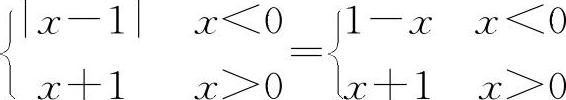 ,当x→0时|f(x)|→1是存在的.
,当x→0时|f(x)|→1是存在的.
5.选C选项【分析】由等价无穷小量的定义,只需计算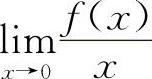 的极限值,即可知选C选项.
的极限值,即可知选C选项.
5.选C选项【分析】由等价无穷小量的定义,只需计算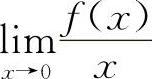 的极限值,即可知选C选项.
的极限值,即可知选C选项.
5.选C选项【分析】由等价无穷小量的定义,只需计算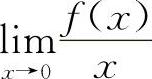 的极限值,即可知选C选项.
的极限值,即可知选C选项.
6.选C选项【分析】因为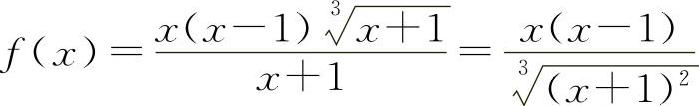 ,只有当x→-1时f(x)→∞,所以选C选项.
,只有当x→-1时f(x)→∞,所以选C选项.
6.选C选项【分析】因为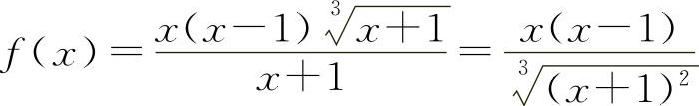 ,只有当x→-1时f(x)→∞,所以选C选项.
,只有当x→-1时f(x)→∞,所以选C选项.
6.选C选项【分析】因为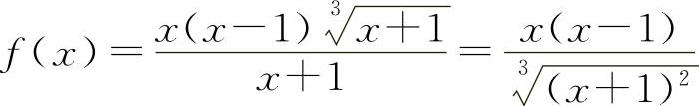 ,只有当x→-1时f(x)→∞,所以选C选项.
,只有当x→-1时f(x)→∞,所以选C选项.
7.【分析】由题设知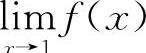 存在,也即极限值存在且为一个确定的常数,因此可设
存在,也即极限值存在且为一个确定的常数,因此可设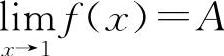 ,则有f(x)=x2-5x-3A
,则有f(x)=x2-5x-3A
7.【分析】由题设知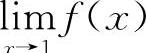 存在,也即极限值存在且为一个确定的常数,因此可设
存在,也即极限值存在且为一个确定的常数,因此可设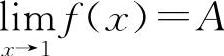 ,则有f(x)=x2-5x-3A
,则有f(x)=x2-5x-3A
7.【分析】由题设知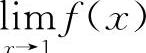 存在,也即极限值存在且为一个确定的常数,因此可设
存在,也即极限值存在且为一个确定的常数,因此可设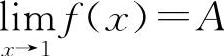 ,则有f(x)=x2-5x-3A
,则有f(x)=x2-5x-3A
将上式两端当x→1时取极限得 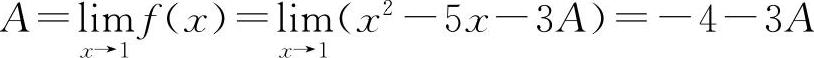
解之得 A=-1,所以 f(x)=x2-5x+3
将上式两端当x→1时取极限得 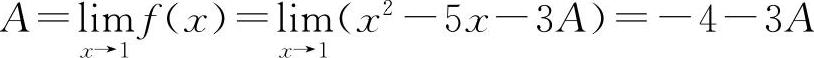
解之得 A=-1,所以 f(x)=x2-5x+3
将上式两端当x→1时取极限得 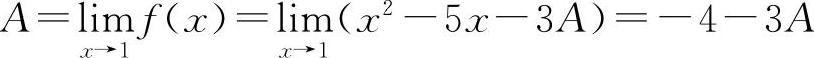
解之得 A=-1,所以 f(x)=x2-5x+3
8.【分析】这两个题目分别为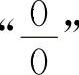 型与
型与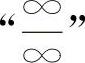 型不定式极限.分别用因式分解消零因子方法和消无穷大因子的方法即可得到解答.(https://www.xing528.com)
型不定式极限.分别用因式分解消零因子方法和消无穷大因子的方法即可得到解答.(https://www.xing528.com)
8.【分析】这两个题目分别为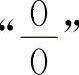 型与
型与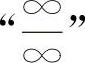 型不定式极限.分别用因式分解消零因子方法和消无穷大因子的方法即可得到解答.
型不定式极限.分别用因式分解消零因子方法和消无穷大因子的方法即可得到解答.
8.【分析】这两个题目分别为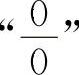 型与
型与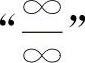 型不定式极限.分别用因式分解消零因子方法和消无穷大因子的方法即可得到解答.
型不定式极限.分别用因式分解消零因子方法和消无穷大因子的方法即可得到解答.
9.【分析】 这4个题目均属于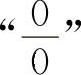 型的不定式极限.对于式中含有根式的应先进行有理化,其他函数尽可能地利用等价无穷小代换以便简化计算.
型的不定式极限.对于式中含有根式的应先进行有理化,其他函数尽可能地利用等价无穷小代换以便简化计算.
9.【分析】 这4个题目均属于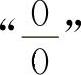 型的不定式极限.对于式中含有根式的应先进行有理化,其他函数尽可能地利用等价无穷小代换以便简化计算.
型的不定式极限.对于式中含有根式的应先进行有理化,其他函数尽可能地利用等价无穷小代换以便简化计算.
9.【分析】 这4个题目均属于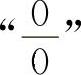 型的不定式极限.对于式中含有根式的应先进行有理化,其他函数尽可能地利用等价无穷小代换以便简化计算.
型的不定式极限.对于式中含有根式的应先进行有理化,其他函数尽可能地利用等价无穷小代换以便简化计算.
10.【分析】 这是“1∞”型不定式极限,应化为重要极限Ⅱ的结构式求解.
10.【分析】 这是“1∞”型不定式极限,应化为重要极限Ⅱ的结构式求解.
10.【分析】 这是“1∞”型不定式极限,应化为重要极限Ⅱ的结构式求解.
11.【分析】此题属于重要极限Ⅱ的反问题,应先求出左边含有常数a的极限值,再求出常数a.
11.【分析】此题属于重要极限Ⅱ的反问题,应先求出左边含有常数a的极限值,再求出常数a.
11.【分析】此题属于重要极限Ⅱ的反问题,应先求出左边含有常数a的极限值,再求出常数a.
则有e3a=27,3a=ln27=3ln3,所以a=ln3.
12.【分析】分子为无穷小量之差,所以不能用等价无穷小量代换.
则有e3a=27,3a=ln27=3ln3,所以a=ln3.
12.【分析】分子为无穷小量之差,所以不能用等价无穷小量代换.
则有e3a=27,3a=ln27=3ln3,所以a=ln3.
12.【分析】分子为无穷小量之差,所以不能用等价无穷小量代换.
解 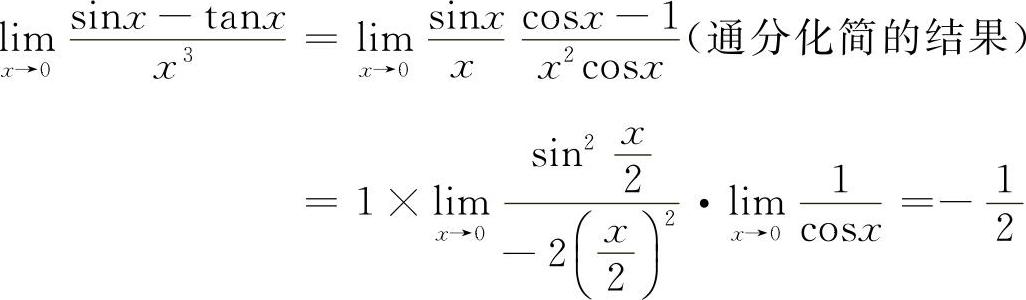
解 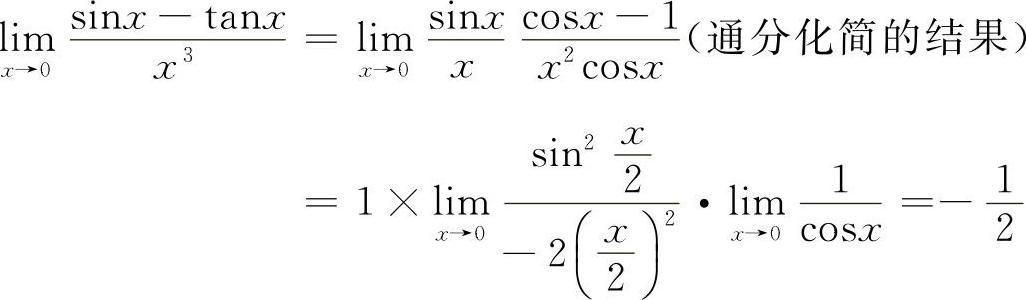
解 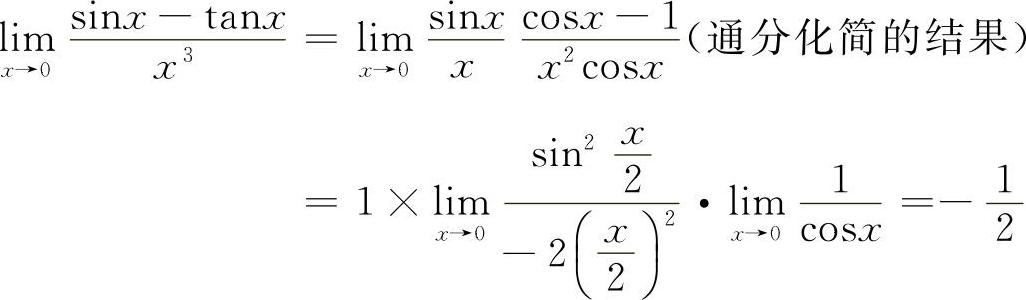
13.【分析】这两个题均为“∞-∞”型不定式,应化为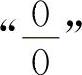 型或
型或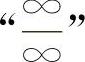 型不定式求解.
型不定式求解.
13.【分析】这两个题均为“∞-∞”型不定式,应化为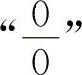 型或
型或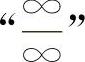 型不定式求解.
型不定式求解.
13.【分析】这两个题均为“∞-∞”型不定式,应化为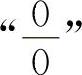 型或
型或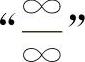 型不定式求解.
型不定式求解.
解 (1)乘上共轭根式,化为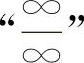 型
型
解 (1)乘上共轭根式,化为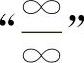 型
型
解 (1)乘上共轭根式,化为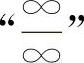 型
型
(2)通分化简,化为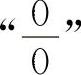 型
型
(2)通分化简,化为 型
型
(2)通分化简,化为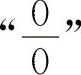 型
型
14.【分析】利用等价无穷小量的定义求解.
14.【分析】利用等价无穷小量的定义求解.
14.【分析】利用等价无穷小量的定义求解.
解 因为 ,所以
,所以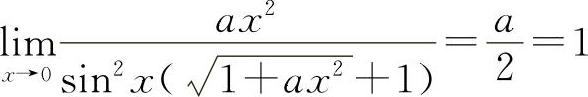 ,即a=2
,即a=2
解 因为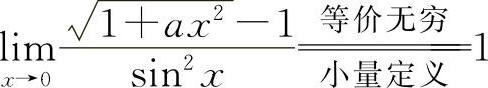 ,所以
,所以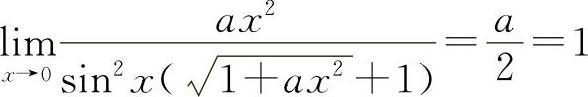 ,即a=2
,即a=2
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




