例1 判定函数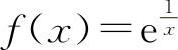 当x→0时的极限是否存在.
当x→0时的极限是否存在.
【分析】因为x→0是指x→0-和x→0+,故应分别计算当x→0时f(x)的左、右极限.
例1 判定函数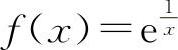 当x→0时的极限是否存在.
当x→0时的极限是否存在.
【分析】因为x→0是指x→0-和x→0+,故应分别计算当x→0时f(x)的左、右极限.
例1 判定函数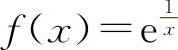 当x→0时的极限是否存在.
当x→0时的极限是否存在.
【分析】因为x→0是指x→0-和x→0+,故应分别计算当x→0时f(x)的左、右极限.
解 当x→0-时,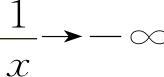 ∞,则
∞,则
解 当x→0-时,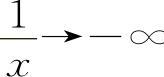 ∞,则
∞,则
解 当x→0-时,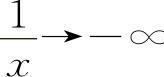 ∞,则
∞,则
当x→0+时,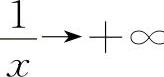 ∞,则
∞,则 ,
,
当x→0+时,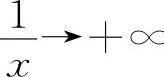 ∞,则
∞,则 ,
,
当x→0+时,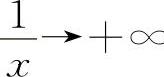 ∞,则
∞,则 ,
,
由定理1.6可知当x→0,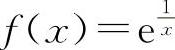 极限不存在.
极限不存在.
例2 在下列函数中,当x→0时,函数f(x)的极限存在的是( ).
由定理1.6可知当x→0,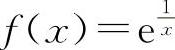 极限不存在.
极限不存在.
例2 在下列函数中,当x→0时,函数f(x)的极限存在的是( ).
由定理1.6可知当x→0,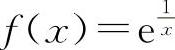 极限不存在.
极限不存在.
例2 在下列函数中,当x→0时,函数f(x)的极限存在的是( ).
【分析】对于分段函数在分段点x=0处的极限,应分别计算f(0-0)和f(0+0),如果f(0-0)=f(0+0)=A,则当x→0时,函数f(x)的极限存在,否则极限不存在.
【分析】对于分段函数在分段点x=0处的极限,应分别计算f(0-0)和f(0+0),如果f(0-0)=f(0+0)=A,则当x→0时,函数f(x)的极限存在,否则极限不存在.
【分析】对于分段函数在分段点x=0处的极限,应分别计算f(0-0)和f(0+0),如果f(0-0)=f(0+0)=A,则当x→0时,函数f(x)的极限存在,否则极限不存在.
在选项A中: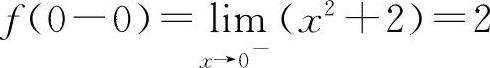 ,
,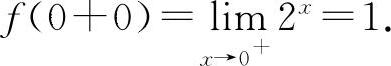 因为f(0-0)≠f(0+0),所以
因为f(0-0)≠f(0+0),所以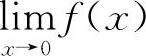 不存在.
不存在.
在选项A中: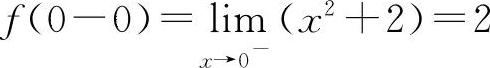 ,
,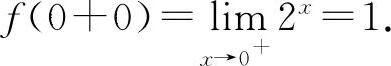 因为f(0-0)≠f(0+0),所以
因为f(0-0)≠f(0+0),所以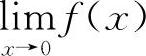 不存在.
不存在.
在选项A中: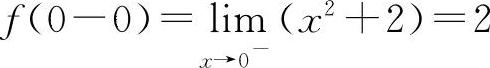 ,
,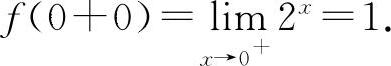 因为f(0-0)≠f(0+0),所以
因为f(0-0)≠f(0+0),所以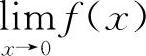 不存在.
不存在.
在选项B中: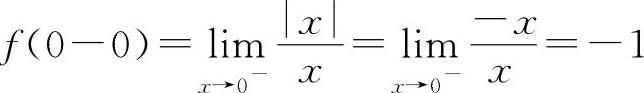 ,
,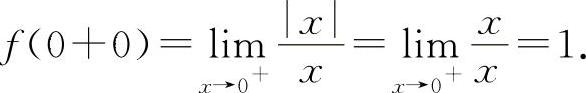 所以
所以 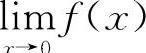 不存在.
不存在.
在选项B中: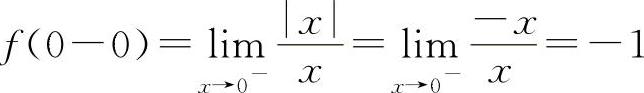 ,
,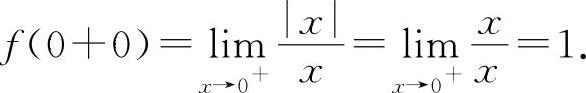 所以
所以 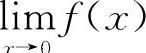 不存在.
不存在.
在选项B中: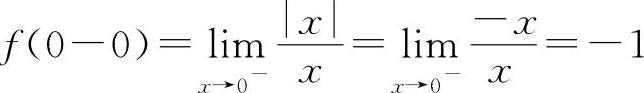 ,
,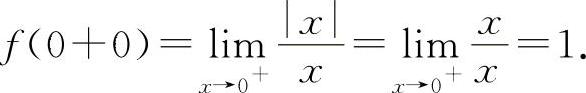 所以
所以 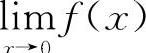 不存在.
不存在.
在选项C中: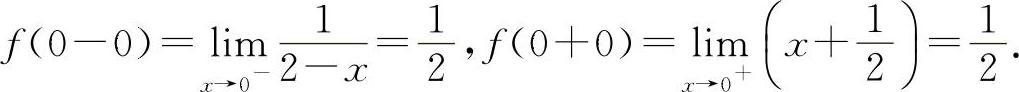 所以
所以 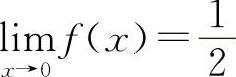 ,故应选C选项.
,故应选C选项.
对于选项D,显然其极限必不存在.
例3 下列极限存在的是( ).
在选项C中: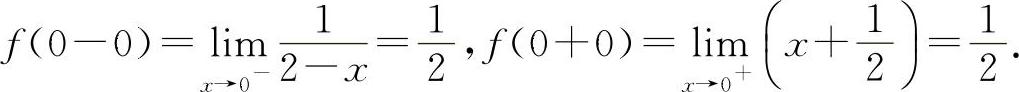 所以
所以 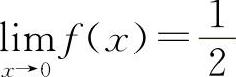 ,故应选C选项.
,故应选C选项.
对于选项D,显然其极限必不存在.
例3 下列极限存在的是( ).
在选项C中: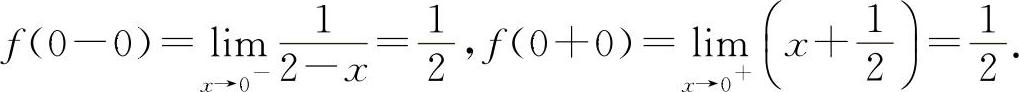 所以
所以 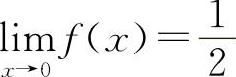 ,故应选C选项.
,故应选C选项.
对于选项D,显然其极限必不存在.
例3 下列极限存在的是( ).
【分析】 当x→+∞时,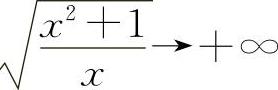 ,极限不存在,排除A选项.
,极限不存在,排除A选项.
【分析】 当x→+∞时,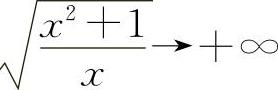 ,极限不存在,排除A选项.
,极限不存在,排除A选项.
【分析】 当x→+∞时,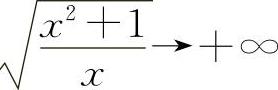 ,极限不存在,排除A选项.
,极限不存在,排除A选项.
对于选项B,当x→+∞时,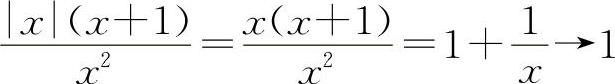 ;而当x→-∞时,
;而当x→-∞时,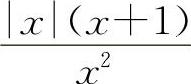
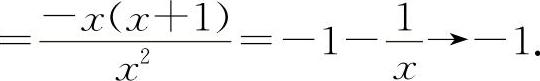 所以当x→∞时,
所以当x→∞时,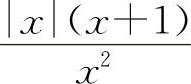 的极限不存在,排除B选项.
的极限不存在,排除B选项.
对于选项B,当x→+∞时,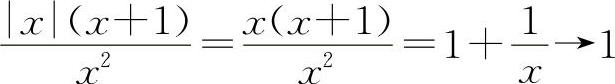 ;而当x→-∞时,
;而当x→-∞时,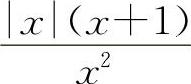
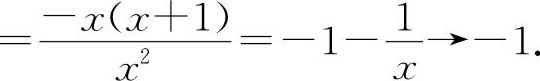 所以当x→∞时,
所以当x→∞时,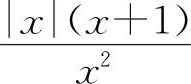 的极限不存在,排除B选项.
的极限不存在,排除B选项.
对于选项B,当x→+∞时,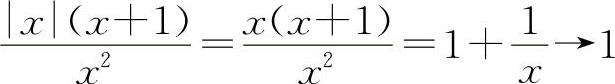 ;而当x→-∞时,
;而当x→-∞时,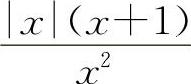
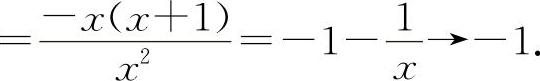 所以当x→∞时,
所以当x→∞时,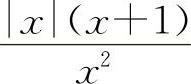 的极限不存在,排除B选项.
的极限不存在,排除B选项.
对选项C,当x→+∞时,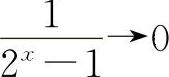 ,所以应选C.
,所以应选C.
显然,对选项D,其极限必不存在.
例4 当x→+∞时,函数y=sinx的极限是否存在,为什么?
对选项C,当x→+∞时,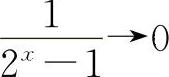 ,所以应选C.
,所以应选C.
显然,对选项D,其极限必不存在.
例4 当x→+∞时,函数y=sinx的极限是否存在,为什么?
对选项C,当x→+∞时,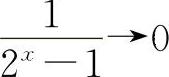 ,所以应选C.
,所以应选C.
显然,对选项D,其极限必不存在.
例4 当x→+∞时,函数y=sinx的极限是否存在,为什么?
【分析】当x→+∞时,x可以取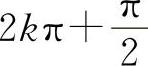 到
到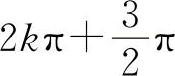 之间的所有值(其中k为正整数且趋于+∞),因此sinx取1到-1之间的所有值,即当x→+∞时,函数y=sinx的极限不存在.我们把它称为:当x→+∞时,sinx振荡无极限.
之间的所有值(其中k为正整数且趋于+∞),因此sinx取1到-1之间的所有值,即当x→+∞时,函数y=sinx的极限不存在.我们把它称为:当x→+∞时,sinx振荡无极限.
例5 下列命题正确的是( ).
A.无穷小量的倒数是无穷大量 B.无穷小量是绝对值很小很小的数
C.无穷小量是以零为极限的变量 D.无界变量一定是无穷大量
【分析】由于数零是无穷小量中唯一的数,所以A不正确,但如果限制无穷小量不取零,则它的倒数为无穷大量.由于绝对值很小很小的“数”其极限值不为零,排除B选项.按无穷小量的定义可知C选项正确.因此D选项必不正确.
【分析】当x→+∞时,x可以取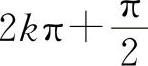 到
到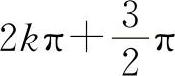 之间的所有值(其中k为正整数且趋于+∞),因此sinx取1到-1之间的所有值,即当x→+∞时,函数y=sinx的极限不存在.我们把它称为:当x→+∞时,sinx振荡无极限.
之间的所有值(其中k为正整数且趋于+∞),因此sinx取1到-1之间的所有值,即当x→+∞时,函数y=sinx的极限不存在.我们把它称为:当x→+∞时,sinx振荡无极限.
例5 下列命题正确的是( ).
A.无穷小量的倒数是无穷大量 B.无穷小量是绝对值很小很小的数
C.无穷小量是以零为极限的变量 D.无界变量一定是无穷大量
【分析】由于数零是无穷小量中唯一的数,所以A不正确,但如果限制无穷小量不取零,则它的倒数为无穷大量.由于绝对值很小很小的“数”其极限值不为零,排除B选项.按无穷小量的定义可知C选项正确.因此D选项必不正确.
【分析】当x→+∞时,x可以取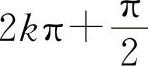 到
到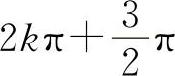 之间的所有值(其中k为正整数且趋于+∞),因此sinx取1到-1之间的所有值,即当x→+∞时,函数y=sinx的极限不存在.我们把它称为:当x→+∞时,sinx振荡无极限.
之间的所有值(其中k为正整数且趋于+∞),因此sinx取1到-1之间的所有值,即当x→+∞时,函数y=sinx的极限不存在.我们把它称为:当x→+∞时,sinx振荡无极限.
例5 下列命题正确的是( ).
A.无穷小量的倒数是无穷大量 B.无穷小量是绝对值很小很小的数
C.无穷小量是以零为极限的变量 D.无界变量一定是无穷大量
【分析】由于数零是无穷小量中唯一的数,所以A不正确,但如果限制无穷小量不取零,则它的倒数为无穷大量.由于绝对值很小很小的“数”其极限值不为零,排除B选项.按无穷小量的定义可知C选项正确.因此D选项必不正确.
例6 若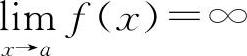 ,
,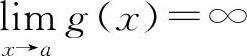 ,则下式中必定成立的是( ).
,则下式中必定成立的是( ).
例6 若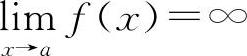 ,
,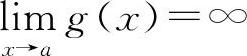 ,则下式中必定成立的是( ).
,则下式中必定成立的是( ).
例6 若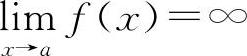 ,
,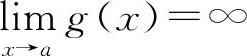 ,则下式中必定成立的是( ).
,则下式中必定成立的是( ).
【分析】因为两个无穷大量之和不一定是无穷大量,例如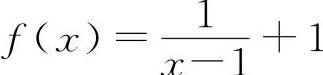 ,
,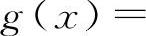
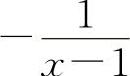 ,当x→1时,都是无穷大量,但f(x)+g(x)=1,所以A与C选项都不一定成立.同理,两个无穷大量之差也不一定是无穷小量.例如,
,当x→1时,都是无穷大量,但f(x)+g(x)=1,所以A与C选项都不一定成立.同理,两个无穷大量之差也不一定是无穷小量.例如,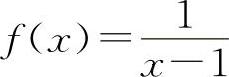 ,
,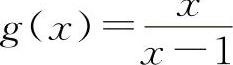 ,当x→1时都是无穷大量,但f(x)-g(x)=-1,所以B选项也不一定成立.选项D显然是正确的.
,当x→1时都是无穷大量,但f(x)-g(x)=-1,所以B选项也不一定成立.选项D显然是正确的.
例7 当x→0时,sin(2x+x2)与x比较是( ).
A.较高阶的无穷小量 B.较低阶的无穷小量
C.等价无穷小量 D.同阶的无穷小量
【分析】两个无穷小量的比较是求它们比的极限.
【分析】因为两个无穷大量之和不一定是无穷大量,例如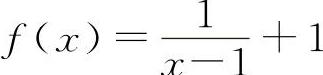 ,
,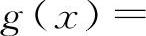
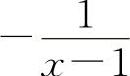 ,当x→1时,都是无穷大量,但f(x)+g(x)=1,所以A与C选项都不一定成立.同理,两个无穷大量之差也不一定是无穷小量.例如,
,当x→1时,都是无穷大量,但f(x)+g(x)=1,所以A与C选项都不一定成立.同理,两个无穷大量之差也不一定是无穷小量.例如,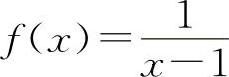 ,
,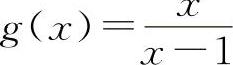 ,当x→1时都是无穷大量,但f(x)-g(x)=-1,所以B选项也不一定成立.选项D显然是正确的.
,当x→1时都是无穷大量,但f(x)-g(x)=-1,所以B选项也不一定成立.选项D显然是正确的.
例7 当x→0时,sin(2x+x2)与x比较是( ).
A.较高阶的无穷小量 B.较低阶的无穷小量
C.等价无穷小量 D.同阶的无穷小量
【分析】两个无穷小量的比较是求它们比的极限.
【分析】因为两个无穷大量之和不一定是无穷大量,例如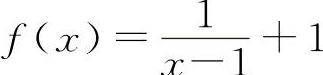 ,
,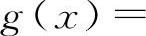
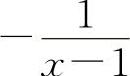 ,当x→1时,都是无穷大量,但f(x)+g(x)=1,所以A与C选项都不一定成立.同理,两个无穷大量之差也不一定是无穷小量.例如,
,当x→1时,都是无穷大量,但f(x)+g(x)=1,所以A与C选项都不一定成立.同理,两个无穷大量之差也不一定是无穷小量.例如,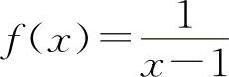 ,
,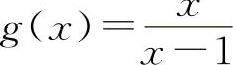 ,当x→1时都是无穷大量,但f(x)-g(x)=-1,所以B选项也不一定成立.选项D显然是正确的.
,当x→1时都是无穷大量,但f(x)-g(x)=-1,所以B选项也不一定成立.选项D显然是正确的.
例7 当x→0时,sin(2x+x2)与x比较是( ).
A.较高阶的无穷小量 B.较低阶的无穷小量
C.等价无穷小量 D.同阶的无穷小量
【分析】两个无穷小量的比较是求它们比的极限.
因为  所以应选D选项.
所以应选D选项.
例8 当x→0时,x2与sinx比较是( ).
A.较高阶的无穷小量 B.较低阶的无穷小量
C.等价无穷小量 D.同阶的无穷小量
【分析】用等价无穷小量代换sinx~x,所以应选A选项.
因为  所以应选D选项.
所以应选D选项.
例8 当x→0时,x2与sinx比较是( ).
A.较高阶的无穷小量 B.较低阶的无穷小量
C.等价无穷小量 D.同阶的无穷小量
【分析】用等价无穷小量代换sinx~x,所以应选A选项.
因为  所以应选D选项.
所以应选D选项.
例8 当x→0时,x2与sinx比较是( ).
A.较高阶的无穷小量 B.较低阶的无穷小量
C.等价无穷小量 D.同阶的无穷小量
【分析】用等价无穷小量代换sinx~x,所以应选A选项.
例9 当x→∞时,f(x)与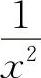 是等价无穷小量,则
是等价无穷小量,则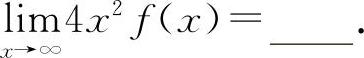
例9 当x→∞时,f(x)与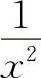 是等价无穷小量,则
是等价无穷小量,则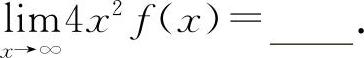
例9 当x→∞时,f(x)与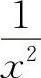 是等价无穷小量,则
是等价无穷小量,则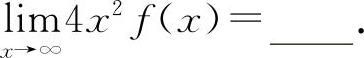
【分析】由等价无穷小的定义有,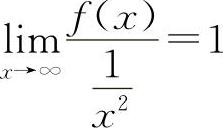 ,因此有
,因此有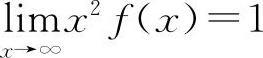 ,则有
,则有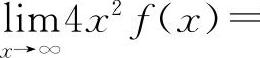
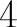 ,所以应填4.
,所以应填4.
【分析】由等价无穷小的定义有,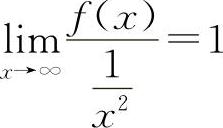 ,因此有
,因此有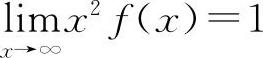 ,则有
,则有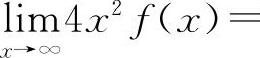
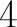 ,所以应填4.
,所以应填4.
【分析】由等价无穷小的定义有,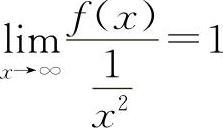 ,因此有
,因此有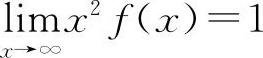 ,则有
,则有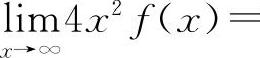
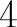 ,所以应填4.
,所以应填4.
例10 当x→0时,若ax2与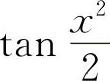 为等价无穷小量,则必有a=.
为等价无穷小量,则必有a=.
例10 当x→0时,若ax2与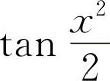 为等价无穷小量,则必有a=.
为等价无穷小量,则必有a=.
例10 当x→0时,若ax2与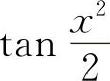 为等价无穷小量,则必有a=.
为等价无穷小量,则必有a=.
【分析】 因为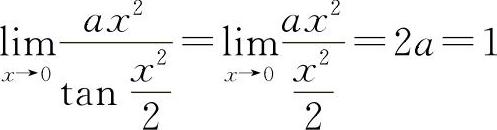 ,所以
,所以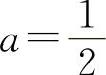 ,应填
,应填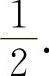
例11 下列极限中,正确的是( ).
【分析】 因为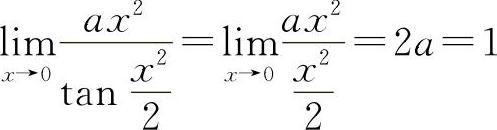 ,所以
,所以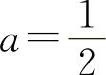 ,应填
,应填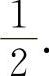
例11 下列极限中,正确的是( ).
【分析】 因为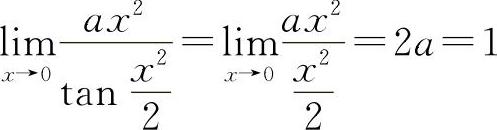 ,所以
,所以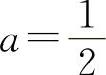 ,应填
,应填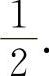
例11 下列极限中,正确的是( ).
【分析】重要极限的结构式也可以理解为 
【分析】重要极限的结构式也可以理解为 
【分析】重要极限的结构式也可以理解为 
其中无穷小量是当 时,方块中的变量是无穷小量.因此A、D选项不正确,选项B因系数为
时,方块中的变量是无穷小量.因此A、D选项不正确,选项B因系数为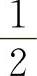 ,所以其极限值为
,所以其极限值为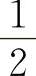 ,因此应选C选项.
,因此应选C选项.
例12 下列等式成立的是( ).
其中无穷小量是当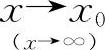 时,方块中的变量是无穷小量.因此A、D选项不正确,选项B因系数为
时,方块中的变量是无穷小量.因此A、D选项不正确,选项B因系数为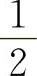 ,所以其极限值为
,所以其极限值为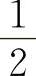 ,因此应选C选项.
,因此应选C选项.
例12 下列等式成立的是( ).
其中无穷小量是当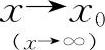 时,方块中的变量是无穷小量.因此A、D选项不正确,选项B因系数为
时,方块中的变量是无穷小量.因此A、D选项不正确,选项B因系数为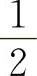 ,所以其极限值为
,所以其极限值为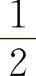 ,因此应选C选项.
,因此应选C选项.
例12 下列等式成立的是( ).
【分析】由于结构式中的方块里的变量必须相同且为无穷小量,所以对选项A有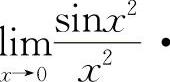
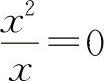 ,对于选项B则有
,对于选项B则有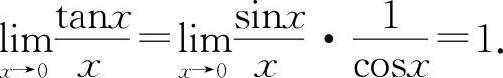 因此选B选项.选项C和D必不正确.
因此选B选项.选项C和D必不正确.
【分析】由于结构式中的方块里的变量必须相同且为无穷小量,所以对选项A有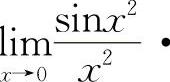
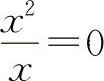 ,对于选项B则有
,对于选项B则有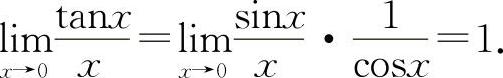 因此选B选项.选项C和D必不正确.
因此选B选项.选项C和D必不正确.
【分析】由于结构式中的方块里的变量必须相同且为无穷小量,所以对选项A有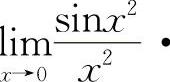
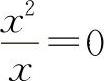 ,对于选项B则有
,对于选项B则有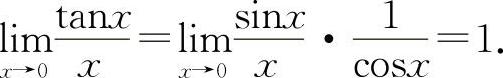 因此选B选项.选项C和D必不正确.
因此选B选项.选项C和D必不正确.
例13 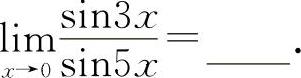
例13 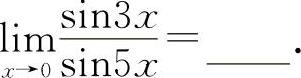
例13 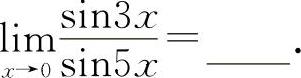
【分析】利用重要极限Ⅰ,则有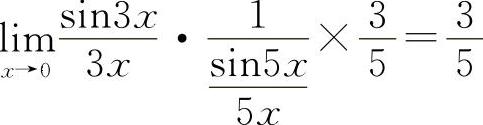 ,所以应填
,所以应填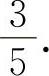
【分析】利用重要极限Ⅰ,则有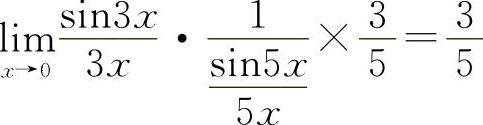 ,所以应填
,所以应填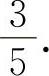
【分析】利用重要极限Ⅰ,则有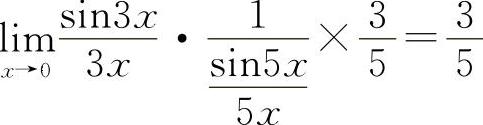 ,所以应填
,所以应填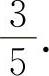
例14 求极限 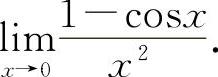 (https://www.xing528.com)
(https://www.xing528.com)
【分析】含三角函数的极限式应优先考虑利用重要极限Ⅰ.
例14 求极限 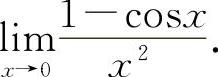
【分析】含三角函数的极限式应优先考虑利用重要极限Ⅰ.
例14 求极限 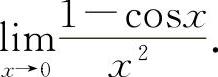
【分析】含三角函数的极限式应优先考虑利用重要极限Ⅰ.
解法一 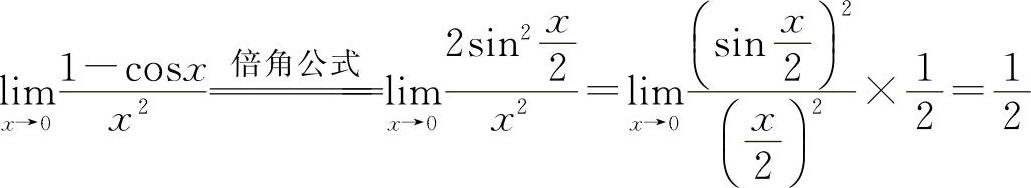
解法一 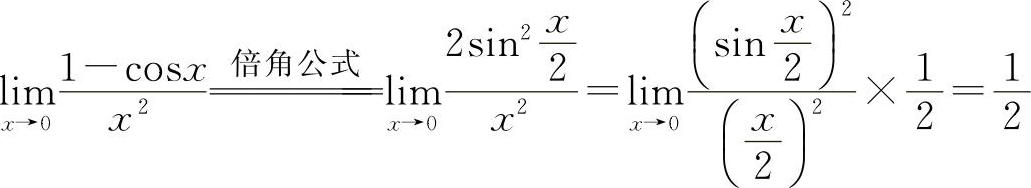
解法一 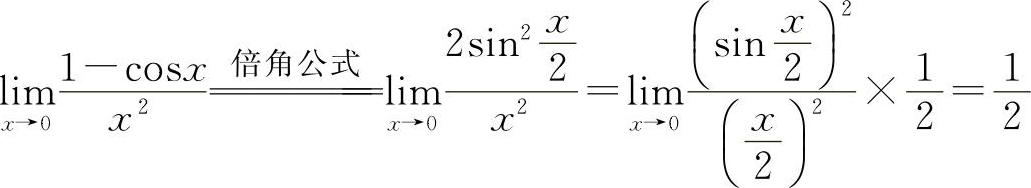
解法二 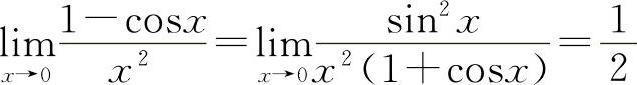
解法二 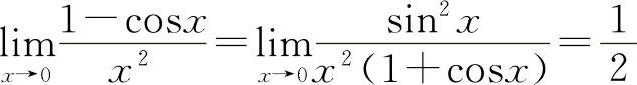
解法二 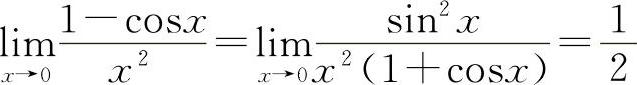
例15 求极限 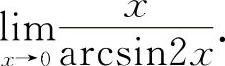
【分析】 含反三角函数式的极限可用变量代换化为三角函数式的重要极限.
例15 求极限 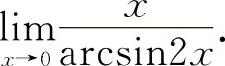
【分析】 含反三角函数式的极限可用变量代换化为三角函数式的重要极限.
例15 求极限 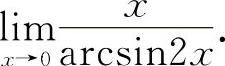
【分析】 含反三角函数式的极限可用变量代换化为三角函数式的重要极限.
解法一 令arcsin2x=t,则2x=sint,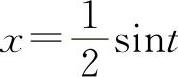 所以
所以 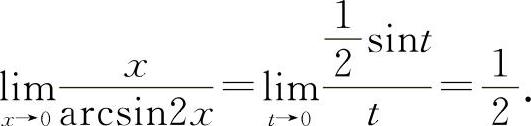
解法二 等价无穷小量代换:arcsin2x~2x(x→0)
解法一 令arcsin2x=t,则2x=sint,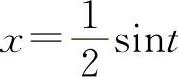 所以
所以 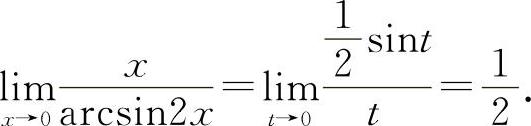
解法二 等价无穷小量代换:arcsin2x~2x(x→0)
解法一 令arcsin2x=t,则2x=sint,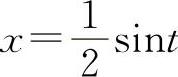 所以
所以 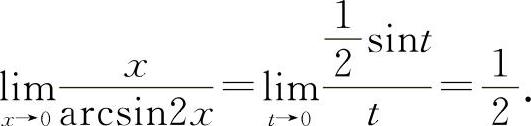
解法二 等价无穷小量代换:arcsin2x~2x(x→0)
所以 
等价无穷小量代换显然比变量代换更为简捷,希望考生能熟练掌握.
例16 下列各极限中,正确的是( ).
所以 
等价无穷小量代换显然比变量代换更为简捷,希望考生能熟练掌握.
例16 下列各极限中,正确的是( ).
所以 
等价无穷小量代换显然比变量代换更为简捷,希望考生能熟练掌握.
例16 下列各极限中,正确的是( ).
【分析】 重要极限Ⅱ的结构式还可以理解为 因此对选项A,
因此对选项A,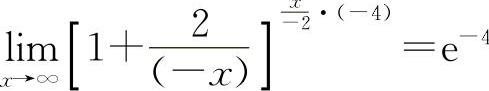 ,选项B显然不正确,而选项C有
,选项B显然不正确,而选项C有 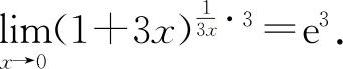 所以应选D选项.
所以应选D选项.
【分析】 重要极限Ⅱ的结构式还可以理解为 因此对选项A,
因此对选项A,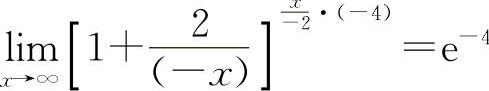 ,选项B显然不正确,而选项C有
,选项B显然不正确,而选项C有 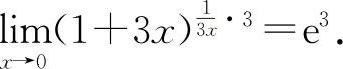 所以应选D选项.
所以应选D选项.
【分析】 重要极限Ⅱ的结构式还可以理解为 因此对选项A,
因此对选项A,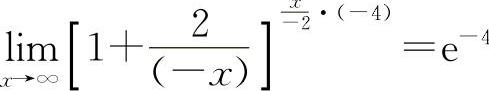 ,选项B显然不正确,而选项C有
,选项B显然不正确,而选项C有 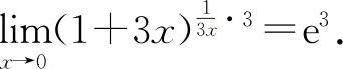 所以应选D选项.
所以应选D选项.
例17 求 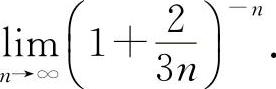
【分析】 利用重要极限Ⅱ.
例17 求 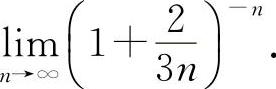
【分析】 利用重要极限Ⅱ.
例17 求 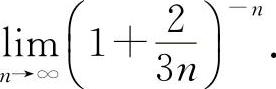
【分析】 利用重要极限Ⅱ.
解 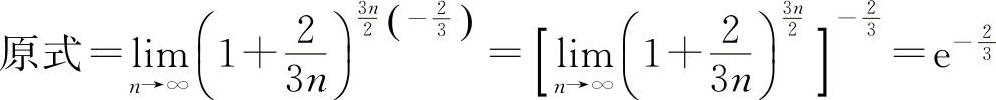
解 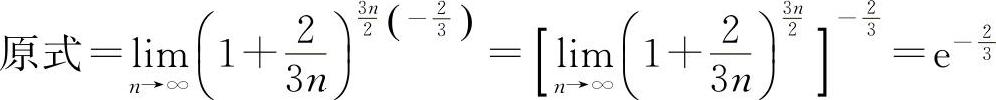
解 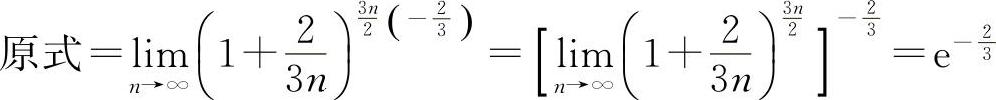
例18 证明: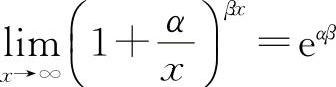 ,其中α,β为不为零的实数.
,其中α,β为不为零的实数.
【分析】 利用重要极限Ⅱ.
例18 证明: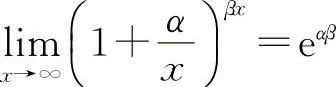 ,其中α,β为不为零的实数.
,其中α,β为不为零的实数.
【分析】 利用重要极限Ⅱ.
例18 证明: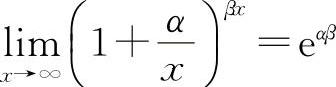 ,其中α,β为不为零的实数.
,其中α,β为不为零的实数.
【分析】 利用重要极限Ⅱ.
证明 因为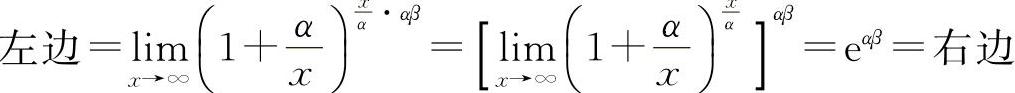
证明 因为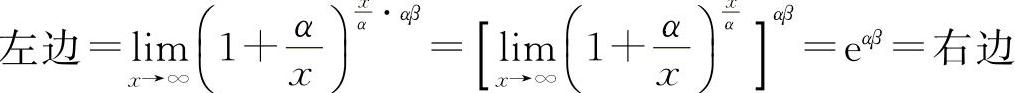
证明 因为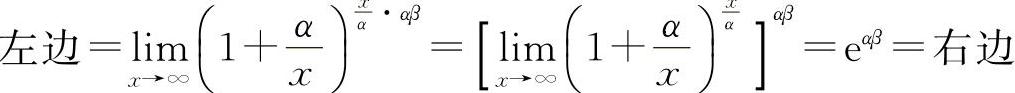
当x→∞时,则有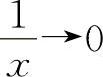 ,因此例18的另一种形式为
,因此例18的另一种形式为 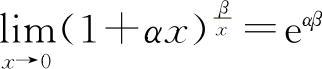
注意:这两个结果可以当公式直接使用,请考生记住.
例19 求下列各题的极限.
当x→∞时,则有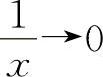 ,因此例18的另一种形式为
,因此例18的另一种形式为 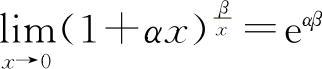
注意:这两个结果可以当公式直接使用,请考生记住.
例19 求下列各题的极限.
当x→∞时,则有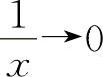 ,因此例18的另一种形式为
,因此例18的另一种形式为 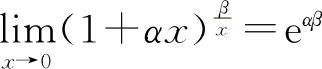
注意:这两个结果可以当公式直接使用,请考生记住.
例19 求下列各题的极限.
【分析】本题的三个极限均属于1∞型不定式,故应利用重要极限Ⅱ求解.
解 (1)将原式写成
【分析】本题的三个极限均属于1∞型不定式,故应利用重要极限Ⅱ求解.
解 (1)将原式写成
【分析】本题的三个极限均属于1∞型不定式,故应利用重要极限Ⅱ求解.
解 (1)将原式写成
(2)注意到重要极限Ⅱ的结构式则有
(2)注意到重要极限Ⅱ的结构式则有
(2)注意到重要极限Ⅱ的结构式则有
(3)注意到题(3)中的底数与题(2)中的底数的关系则有
(3)注意到题(3)中的底数与题(2)中的底数的关系则有
(3)注意到题(3)中的底数与题(2)中的底数的关系则有
本题也可以用下面的方法求解
本题也可以用下面的方法求解
本题也可以用下面的方法求解
例20 设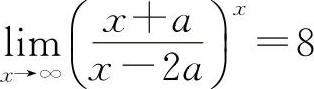 ,求常数a.
,求常数a.
【分析】 此例属于重要极限Ⅱ的反问题.
例20 设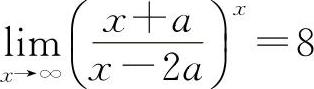 ,求常数a.
,求常数a.
【分析】 此例属于重要极限Ⅱ的反问题.
例20 设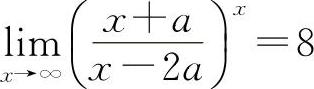 ,求常数a.
,求常数a.
【分析】 此例属于重要极限Ⅱ的反问题.
解 由于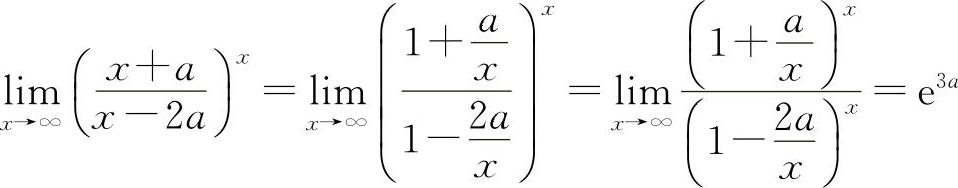 ,由题意可知e3a=8,3a=ln8=3ln2,所以a=ln2.
,由题意可知e3a=8,3a=ln8=3ln2,所以a=ln2.
解 由于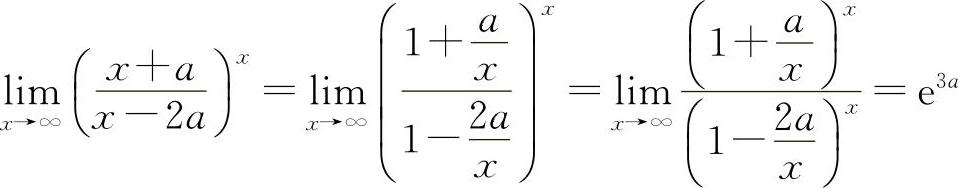 ,由题意可知e3a=8,3a=ln8=3ln2,所以a=ln2.
,由题意可知e3a=8,3a=ln8=3ln2,所以a=ln2.
解 由于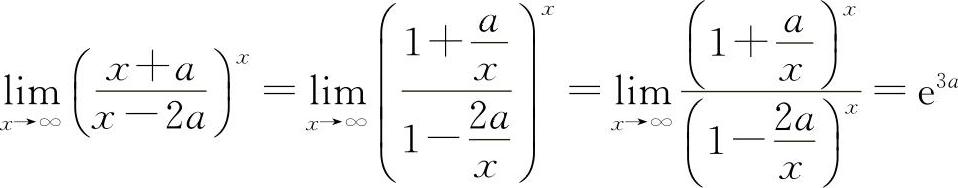 ,由题意可知e3a=8,3a=ln8=3ln2,所以a=ln2.
,由题意可知e3a=8,3a=ln8=3ln2,所以a=ln2.
例21 求下列函数的极限(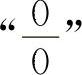 型不定式).
型不定式).
例21 求下列函数的极限(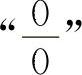 型不定式).
型不定式).
例21 求下列函数的极限(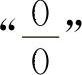 型不定式).
型不定式).
【分析】 上述两题的分子与分母都以零为极限,这类题目称为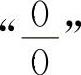 型不定式,是极限计算中基本的也是十分重要的类型.商的极限运算法则不适用,但是,注意到x→x0即(x-x0)→0,但x-x0≠0这一实质,可以消去分子与分母中的零因子而求得极限.这种方法通常称为消去零因子法.
型不定式,是极限计算中基本的也是十分重要的类型.商的极限运算法则不适用,但是,注意到x→x0即(x-x0)→0,但x-x0≠0这一实质,可以消去分子与分母中的零因子而求得极限.这种方法通常称为消去零因子法.
【分析】 上述两题的分子与分母都以零为极限,这类题目称为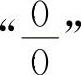 型不定式,是极限计算中基本的也是十分重要的类型.商的极限运算法则不适用,但是,注意到x→x0即(x-x0)→0,但x-x0≠0这一实质,可以消去分子与分母中的零因子而求得极限.这种方法通常称为消去零因子法.
型不定式,是极限计算中基本的也是十分重要的类型.商的极限运算法则不适用,但是,注意到x→x0即(x-x0)→0,但x-x0≠0这一实质,可以消去分子与分母中的零因子而求得极限.这种方法通常称为消去零因子法.
【分析】 上述两题的分子与分母都以零为极限,这类题目称为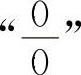 型不定式,是极限计算中基本的也是十分重要的类型.商的极限运算法则不适用,但是,注意到x→x0即(x-x0)→0,但x-x0≠0这一实质,可以消去分子与分母中的零因子而求得极限.这种方法通常称为消去零因子法.
型不定式,是极限计算中基本的也是十分重要的类型.商的极限运算法则不适用,但是,注意到x→x0即(x-x0)→0,但x-x0≠0这一实质,可以消去分子与分母中的零因子而求得极限.这种方法通常称为消去零因子法.
解 (1)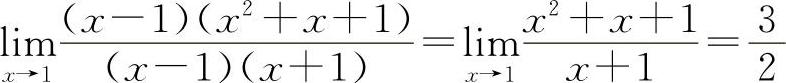
(2)分式中含有根式的零因子时,通常乘以其共轭根式.
解 (1)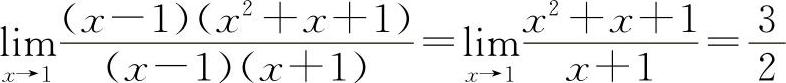
(2)分式中含有根式的零因子时,通常乘以其共轭根式.
解 (1)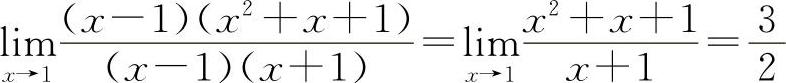
(2)分式中含有根式的零因子时,通常乘以其共轭根式.
例22 求下列函数的极限
例22 求下列函数的极限
例22 求下列函数的极限
【分析】 这三题的分子与分母都趋于∞,称为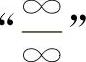 型不定式,也是极限计算中基本的和十分重要的类型之一.基本解法之一是消去“∞”因子,通常是分别提取分子与分母中最高阶无穷因子.
型不定式,也是极限计算中基本的和十分重要的类型之一.基本解法之一是消去“∞”因子,通常是分别提取分子与分母中最高阶无穷因子.
【分析】 这三题的分子与分母都趋于∞,称为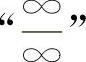 型不定式,也是极限计算中基本的和十分重要的类型之一.基本解法之一是消去“∞”因子,通常是分别提取分子与分母中最高阶无穷因子.
型不定式,也是极限计算中基本的和十分重要的类型之一.基本解法之一是消去“∞”因子,通常是分别提取分子与分母中最高阶无穷因子.
【分析】 这三题的分子与分母都趋于∞,称为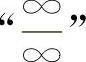 型不定式,也是极限计算中基本的和十分重要的类型之一.基本解法之一是消去“∞”因子,通常是分别提取分子与分母中最高阶无穷因子.
型不定式,也是极限计算中基本的和十分重要的类型之一.基本解法之一是消去“∞”因子,通常是分别提取分子与分母中最高阶无穷因子.
解 (1)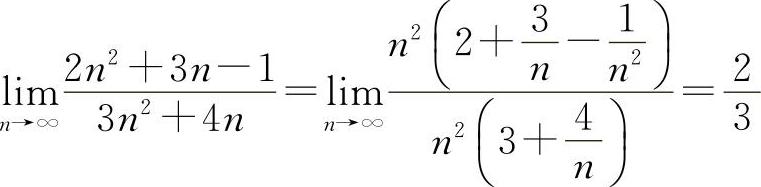
解 (1)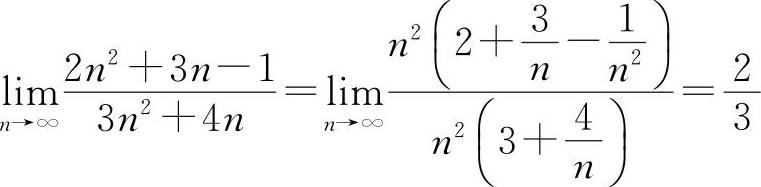
解 (1)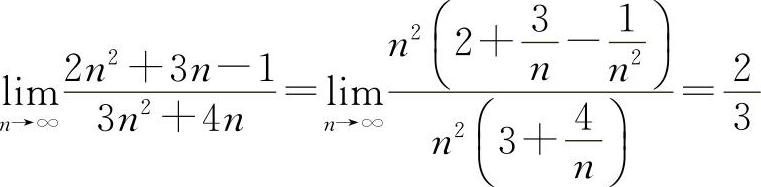
(3)利用等差数列的求和公式,再消去“∞”因子.
(3)利用等差数列的求和公式,再消去“∞”因子.
(3)利用等差数列的求和公式,再消去“∞”因子.
例23 求下列函数的极限(“∞-∞”型不定式).
例23 求下列函数的极限(“∞-∞”型不定式).
例23 求下列函数的极限(“∞-∞”型不定式).
【分析】这是“∞-∞”型的不定式,必须化为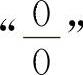 型或
型或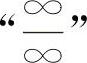 型不定式求解.常用的方法有通分化简和根式有理化等.
型不定式求解.常用的方法有通分化简和根式有理化等.
【分析】这是“∞-∞”型的不定式,必须化为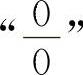 型或
型或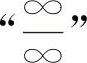 型不定式求解.常用的方法有通分化简和根式有理化等.
型不定式求解.常用的方法有通分化简和根式有理化等.
【分析】这是“∞-∞”型的不定式,必须化为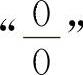 型或
型或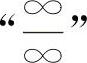 型不定式求解.常用的方法有通分化简和根式有理化等.
型不定式求解.常用的方法有通分化简和根式有理化等.
解 (1)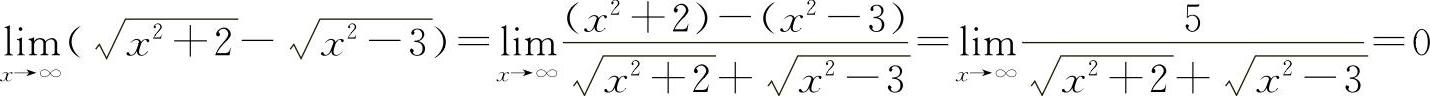
解 (1)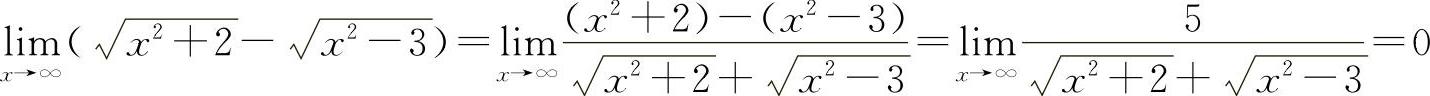
解 (1)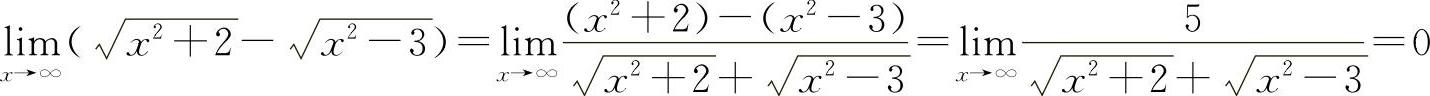
例24 计算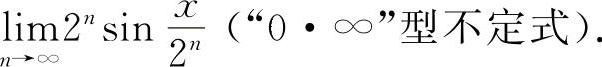
例24 计算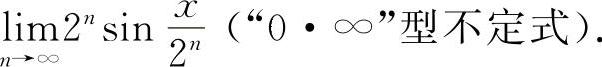
例24 计算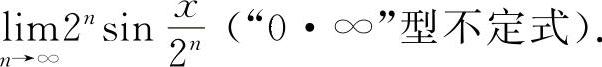
【分析】这类“0·∞”型的不定式应化为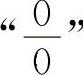 型或
型或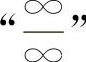 型,也可以用等价无穷小量代换求解.
型,也可以用等价无穷小量代换求解.
【分析】这类“0·∞”型的不定式应化为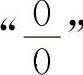 型或
型或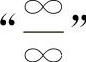 型,也可以用等价无穷小量代换求解.
型,也可以用等价无穷小量代换求解.
【分析】这类“0·∞”型的不定式应化为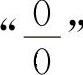 型或
型或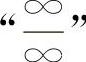 型,也可以用等价无穷小量代换求解.
型,也可以用等价无穷小量代换求解.
解法一 化为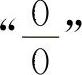 型,用重要极限Ⅰ计算.
型,用重要极限Ⅰ计算.
解法一 化为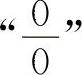 型,用重要极限Ⅰ计算.
型,用重要极限Ⅰ计算.
解法一 化为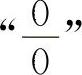 型,用重要极限Ⅰ计算.
型,用重要极限Ⅰ计算.
解法二 用等价无穷小量代换.
解法二 用等价无穷小量代换.
解法二 用等价无穷小量代换.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




