【摘要】:1.复合函数定义 设y是u的函数 y=f(u)而u又是x的函数 u=φ(x)又设X表示函数u=φ(x)的定义域的一个子集,如果对于X上的每一个取值x所对应的u值,函数y=f(u)有定义,则y通过u=φ(x)而成为x的函数,记为y=f(φ(x))这个函数叫做由函数y=f(u)及u=φ(x)复合而成的复合函数,它的定义域为X,u叫做中间变量.所以,复合函数实际就是将中间变量代入后所构成的函数.注意:不
1.复合函数
定义 设y是u的函数 y=f(u)而u又是x的函数 u=φ(x)
又设X表示函数u=φ(x)的定义域的一个子集,如果对于X上的每一个取值x所对应的u值,函数y=f(u)有定义,则y通过u=φ(x)而成为x的函数,记为
y=f(φ(x))
这个函数叫做由函数y=f(u)及u=φ(x)复合而成的复合函数,它的定义域为X,u叫做中间变量.
所以,复合函数实际就是将中间变量代入后所构成的函数.
注意:不是任何两个函数都可以复合成一个复合函数的,例如,函数y=arcsinu及u=x2+3就不能复合成一个复合函数.因为对于u=x2+3的定义域(-∞,+∞)内的任何值x所对应的u值(都大于或等于3),y=arcsinu都没有定义.(https://www.xing528.com)
复合函数不仅可以有一个中间变量,还可以有更多的中间变量,如u,v,w,t等.
在求函数的导数时,我们往往要反过来考虑问题,即一个函数是由哪几个基本初等函数(或简单函数)复合而成的.
2.初等函数
所谓初等函数是指由基本初等函数经过有限次的四则运算(加、减、乘、除)和复合所构成且能用一个分析式表示的函数.例如,函数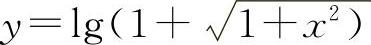 ,y
,y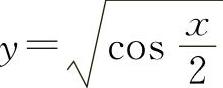 ,
,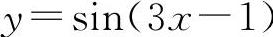 ,y=cos2(lnx)等都是初等函数.
,y=cos2(lnx)等都是初等函数.
所谓初等函数是指由基本初等函数经过有限次的四则运算(加、减、乘、除)和复合所构成且能用一个分析式表示的函数.例如,函数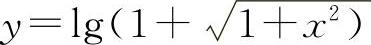 ,y
,y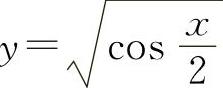 ,
,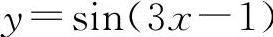 ,y=cos2(lnx)等都是初等函数.
,y=cos2(lnx)等都是初等函数.
所谓初等函数是指由基本初等函数经过有限次的四则运算(加、减、乘、除)和复合所构成且能用一个分析式表示的函数.例如,函数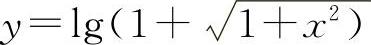 ,y
,y ,
,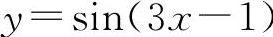 ,y=cos2(lnx)等都是初等函数.
,y=cos2(lnx)等都是初等函数.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




