1.常数
y=C
它的定义域是(-∞,+∞),图形是一条平行于x轴的直线.
2.幂函数
y=xμ(μ为实数)
它的定义域随μ值的不同而不同,但不管μ的值是多少,它在(0,+∞)内总是有定义的.
当μ>0时,它的图形如图1-1所示,不论μ为何值,它的图形都经过原点(0,0)和点(1,1),在(0,+∞)内严格单调增加且无界.
当μ<0时,它的图形如图1-2所示,在(0,+∞)内严格单调减少且无界,曲线以x轴和y轴为渐近线,都经过点(1,1).
图 1-1
图 1-2
3.指数函数
y=ax(a>0,a≠1)
它的定义域是(-∞,+∞),由于不论x为何值,总有ax>0,且a0=1,所以它的图形总是在x轴的上方,且经过点(0,1).
当a>1时,函数严格单调增加且无界,曲线以x轴的负半轴为渐近线.
当0<a<1时,函数严格单调减少且无界,曲线以x轴的正半轴为渐近线,如图1-3所示.
以无理数e=2.7182818…为底的指数函数y=ex是微积分中常用的指数函数.
4.对数函数
y=logax(a>0,a≠1)
它的定义域为(0,+∞),不论a为何值,对数函数的图形都经过点(1,0).
图 1-3
当a>1时,函数严格单调增加且无界,曲线以y轴的负半轴为渐近线.
当0<a<1时,函数严格单调减少且无界,曲线以y轴的正半轴为渐近线,如图1-4所示.
以无理数e为底的对数函数y=logex叫自然对数,简记为y=lnx.
自然对数在微积分中是比较常用的.
5.三角函数
常用的三角函数有以下四个:
y=sinxy=cosxy=tanxy=cotx
在微积分中,三角函数的自变量x一律以“rad(弧度)”为单位.例如x=1,就表示x等于1rad(57°17'44.8″).
函数y=sinx的定义域为(-∞,+∞),是奇函数,且是周期等于2π的周期函数,其图形如图1-5所示.
函数y=cosx的定义域为(-∞,+∞),是偶函数,且是周期等于2π的周期函数,其图形如图1-6所示.
图 1-4
图 1-5(https://www.xing528.com)
图 1-6
因为|sinx|≤1,|cosx|≤1,所以它们都是有界函数.
函数y=tanx的定义域是除去点 的其他实数.它是奇函数,且是周期为π的周期函数,其图形如图1-7所示.
的其他实数.它是奇函数,且是周期为π的周期函数,其图形如图1-7所示.
函数y=cotx的定义域是除去点x=kπ(k=0,±1,±2,…)的其他实数.它是奇函数,且是周期为π的周期函数,其图形如图1-8所示.
它们是作为相应三角函数的反函数定义的.由于y=sinx,y=cosx在定义域内不单调,它们的反函数不唯一,所以对于y=sinx,只考虑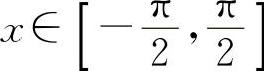 ,对于y=cosx,只考虑x∈[0,π],以使它们单调,并使其反函数存在.此时我们称反正弦函数和反余弦函数取主值,即
,对于y=cosx,只考虑x∈[0,π],以使它们单调,并使其反函数存在.此时我们称反正弦函数和反余弦函数取主值,即
 ,0≤arccosx≤π,它们的图形分别为图1-9和图1-10中的实线部分.
,0≤arccosx≤π,它们的图形分别为图1-9和图1-10中的实线部分.
y=arcsinx和y=arccosx的定义域都是[-1,1].
它们是作为相应三角函数的反函数定义的.由于y=sinx,y=cosx在定义域内不单调,它们的反函数不唯一,所以对于y=sinx,只考虑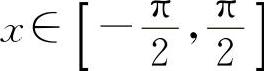 ,对于y=cosx,只考虑x∈[0,π],以使它们单调,并使其反函数存在.此时我们称反正弦函数和反余弦函数取主值,即
,对于y=cosx,只考虑x∈[0,π],以使它们单调,并使其反函数存在.此时我们称反正弦函数和反余弦函数取主值,即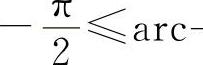
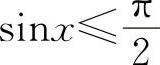 ,0≤arccosx≤π,它们的图形分别为图1-9和图1-10中的实线部分.
,0≤arccosx≤π,它们的图形分别为图1-9和图1-10中的实线部分.
y=arcsinx和y=arccosx的定义域都是[-1,1].
图 1-7
图 1-8
6.反三角函数
常见的反三角函数有以下四个:
y=arcsinxy=arccosxy=arctanxy=arccotx
它们是作为相应三角函数的反函数定义的.由于y=sinx,y=cosx在定义域内不单调,它们的反函数不唯一,所以对于y=sinx,只考虑 ,对于y=cosx,只考虑x∈[0,π],以使它们单调,并使其反函数存在.此时我们称反正弦函数和反余弦函数取主值,即
,对于y=cosx,只考虑x∈[0,π],以使它们单调,并使其反函数存在.此时我们称反正弦函数和反余弦函数取主值,即
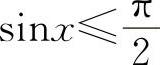 ,0≤arccosx≤π,它们的图形分别为图1-9和图1-10中的实线部分.
,0≤arccosx≤π,它们的图形分别为图1-9和图1-10中的实线部分.
y=arcsinx和y=arccosx的定义域都是[-1,1].
同理,对于反正切函数y=arctanx,也取主值 ,即
,即 ,对于反余切函数y=arccotx取主值(0,π),即0<arccotx<π,它们的定义域均为(-∞,+∞),它们的图形分别为图1-11和图1-12中的实线部分.
,对于反余切函数y=arccotx取主值(0,π),即0<arccotx<π,它们的定义域均为(-∞,+∞),它们的图形分别为图1-11和图1-12中的实线部分.
同理,对于反正切函数y=arctanx,也取主值 ,即
,即 ,对于反余切函数y=arccotx取主值(0,π),即0<arccotx<π,它们的定义域均为(-∞,+∞),它们的图形分别为图1-11和图1-12中的实线部分.
,对于反余切函数y=arccotx取主值(0,π),即0<arccotx<π,它们的定义域均为(-∞,+∞),它们的图形分别为图1-11和图1-12中的实线部分.
同理,对于反正切函数y=arctanx,也取主值 ,即
,即 ,对于反余切函数y=arccotx取主值(0,π),即0<arccotx<π,它们的定义域均为(-∞,+∞),它们的图形分别为图1-11和图1-12中的实线部分.
,对于反余切函数y=arccotx取主值(0,π),即0<arccotx<π,它们的定义域均为(-∞,+∞),它们的图形分别为图1-11和图1-12中的实线部分.
图 1-9
图 1-9
图 1-9
图 1-10
图 1-10
图 1-10
图 1-11
图 1-11
图 1-11
图 1-12
图 1-12
图 1-12
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




