高数- 显函数、分段函数、隐函数

（1）显函数函数关系用解析式y=f（x）表示的称为显函数，如y=x²sinx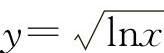，等.

（2）分段函数有时还要考察这样的函数，对于其定义域内自变量x的不同值，函数不能用一个统一的公式表示，而要用两个或两个以上的公式来表示.这类函数称为“分段函数”.

例如，函数y=|x|就是一个分段函数，它可以写成

（1）显函数函数关系用解析式y=f（x）表示的称为显函数，如y=x²sinx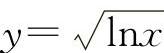，等.

（2）分段函数有时还要考察这样的函数，对于其定义域内自变量x的不同值，函数不能用一个统一的公式表示，而要用两个或两个以上的公式来表示.这类函数称为“分段函数”.

例如，函数y=|x|就是一个分段函数，它可以写成

当x＜0时，用公式y=-x来表示；当x≥0时，用公式y=x来表示.这个函数的定义域是（-∞，+∞）.

关于分段函数，要注意以下几点：

1）分段函数是用几个公式合起来表示一个函数，而不是表示几个函数.

2）因为函数式子是分段表示的，所以各段的定义域必须明确标出.

3）对分段函数求函数值时，不同点的函数值应代入相应范围的公式中去求.

4）分段函数的定义域是各项定义域的并集.

（3）隐函数前面所讲的形如y=f（x）的函数，一般称为显函数.显函数的特点是因变量y单独地在等号的一边（左边），而另一边（右边）则仅仅是自变量x的表达式f（x）.此外，还有一类函数，称为隐函数.

定义 凡能够由方程F（x，y）=0确定的函数关系，就称之为隐函数.

例如，x²+y²-1=0就是一个隐函数，因为在这个方程中，函数y没有用仅含自变量x的公式f（x）表示出来.不过若由它解出(www.xing528.com)

当x＜0时，用公式y=-x来表示；当x≥0时，用公式y=x来表示.这个函数的定义域是（-∞，+∞）.

关于分段函数，要注意以下几点：

1）分段函数是用几个公式合起来表示一个函数，而不是表示几个函数.

2）因为函数式子是分段表示的，所以各段的定义域必须明确标出.

3）对分段函数求函数值时，不同点的函数值应代入相应范围的公式中去求.

4）分段函数的定义域是各项定义域的并集.

（3）隐函数前面所讲的形如y=f（x）的函数，一般称为显函数.显函数的特点是因变量y单独地在等号的一边（左边），而另一边（右边）则仅仅是自变量x的表达式f（x）.此外，还有一类函数，称为隐函数.

定义 凡能够由方程F（x，y）=0确定的函数关系，就称之为隐函数.

例如，x²+y²-1=0就是一个隐函数，因为在这个方程中，函数y没有用仅含自变量x的公式f（x）表示出来.不过若由它解出

或 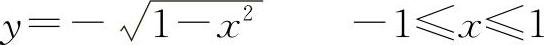它就变成了两个显函数（称每一个显函数为一个单值分支，前一支表示上半圆，后一支表示下半圆），并称该隐函数为二值函数（多值函数的一种）.

要注意的是：并非所有隐函数都可以解成显函数.例如，方程e^xy-x²-xy-1=0就不能解成显函数.

或 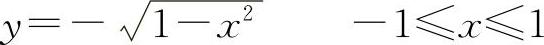它就变成了两个显函数（称每一个显函数为一个单值分支，前一支表示上半圆，后一支表示下半圆），并称该隐函数为二值函数（多值函数的一种）.

要注意的是：并非所有隐函数都可以解成显函数.例如，方程e^xy-x²-xy-1=0就不能解成显函数.