1.Boosting类算法概述
Boosting是一种提高任意给定学习算法准确度的通用机器学习算法,Boosting的思想起源于1984年Valiant提出的“可能近似正确”—PAC(Probably Approximately Correct)学习模型。在PAC模型中,Valiant和Kearns提出了弱学习算法和强学习算法。其概念是:如果一个学习算法通过学习一组样本,识别错误率小于1/2,即准确率仅比随机猜测略高的学习算法,则该算法属于弱学习算法;反之,如果识别率很高,则该算法属于强学习算法。1989年,Valiant和Kearns首次提出了PAC学习模型中弱学习算法和强学习算法的等价性问题,即任意给定仅比随机猜测略好的弱学习算法(准确率大于0.5),是否可以将其提升为强学习算法?如果二者等价,那么只需找到一个比随机猜测略好的弱学习算法就可以将其提升为强学习算法,而不必寻找很难获得的强学习算法。1990年,Schapire最先构造出一种多项式级的算法来将任意一个弱学习算法提升到一个任意正确率的强学习算法,这就是最初的Boosting算法。一年后,Freund提出了一种效率更高的Boosting算法。但是,这两种算法存在共同的实践上的缺陷,那就是都要求事先知道弱学习算法学习正确的下限。1995年,Freund和Schapire改进了Boosting算法,提出了AdaBoost算法,该算法效率和Freund于1991年提出的Boosting算法几乎相同,但不需要任何关于弱学习器的先验知识,因而更容易应用到实际问题当中。之后,Freund和Schapire进一步提出了改变Boosting投票权重的AdaBoost.M1、Ada-Boost.M2等算法,在机器学习领域受到了极大的关注。
Boosting方法是一种用来提高弱分类算法准确度的方法,这种方法通过构造一个预测函数系列,然后以一定的方式将它们组合成一个预测函数。它是一种框架算法,主要是通过对样本集的操作获得样本子集,然后用弱分类算法在样本子集上训练生成一系列的基分类器。它可以用来提高其他弱分类算法的识别率,也就是将其他的弱分类算法作为基分类算法放于Boosting框架中,通过Boosting框架对训练样本集的操作,得到不同的训练样本子集,用该样本子集去训练生成基分类器。每得到一个样本集就用该基分类算法在该样本集上产生一个基分类器,这样在给定训练轮数n后,就可产生n个基分类器,然后Boosting框架算法将这n个基分类器进行加权融合,产生一个最后的结果分类器,在这n个基分类器中,每个单个的分类器的识别率不一定很高,但它们联合后的结果有很高的识别率,这样便提高了该弱分类算法的识别率。在产生单个的基分类器时可用相同的分类算法,也可用不同的分类算法,这些算法一般是不稳定的弱分类算法,如神经网络(BP)、决策树(C4.5)等。
与Bagging算法可以并行训练多个弱分类器不同,Boosting算法中的弱分类器是以串行的方式训练得到的,其基本思想为:算法会为每个训练样本赋予一个权值。每次用训练完的新分类器标注各个样本,若某个样本点已被分类正确,则将其权值降低,并以该权重进行下一次数据的抽样(抽中的概率减小);若样本点未被正确分类,则提高其权值,并以该权重进行下一次数据的抽样(抽中的概率增大)。权值越高的样本在下一次训练中所占的比重越大,也就是说越难区分的样本在训练过程中会变得越来越重要。整个迭代过程直到错误率足够小或达到一定次数才停止。Bagging使用多数投票或平均的策略来组合多个基分类器,相当于每一个基分类器具有相同的权重;而Boosting则根据基分类器的预测性能,给予不同的基分类器不同的权重,即:如果一个基分类器的误差越高,则该基分类器的权重越低[31]。Boosting算法原理见图5-24所示。
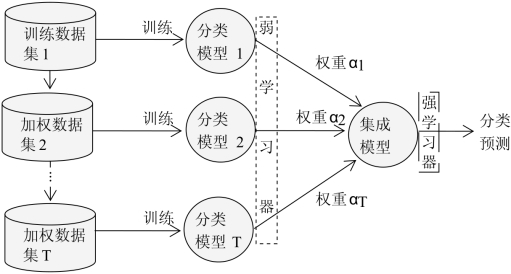
图5-24 Boosting算法原理图
Boosting算法在实际应用时有一个明显的缺陷,即要预先知道弱分类器的误差上界,这在实际问题中是很难确定的。1995年,Freund和Schapire提出了著名的AdaBoost算法,该算法不需要预先知道弱分类器的误差上界,在实际问题中应用广泛。AdaBoost算法是Boosting类算法中的经典代表。
2.AdaBoost算法流程
AdaBoost通过改变样本的分布突出被错误分类的样本上,并进而训练弱分类器得到弱分类器的权重,根据权重整合在一起得到最终的强分类器。AdaBoost方法大致有:Discrete AdaBoost、Real AdaBoost、LogitBoost和Gentle AdaBoost,所有的方法训练的框架的都是相似的。通常使用最多的应该是Discrete AdaBoost(离散的AdaBoost)即Ada-Boost.M1算法,主要因为它的简单却不俗的表现。
AdaBoost.M1算法的形式化描述如下:

3.Boosting算法特点(https://www.xing528.com)
对于Boosting算法,需要解决两个问题:
(1)如何调整训练集,使得在训练集上训练的弱分类器得以进行;
(2)如何将训练得到的各个弱分类器联合起来形成强分类器。
Boosting算法的主要特点有:
(1)Boosting是一种框架算法,拥有系列算法,如AdaBoost、GradientBoosting、LogitBoost等算法;
(2)可以提高任意给定学习算法的准确度;
(3)训练过程为阶梯状,弱分类器按次序一一进行训练(实现上可以做到并行),弱分类器的训练集按照某种策略每次都进行一定的转化,最后以一定的方式将弱分类器组合成一个强分类器;
(4)Boosting中所有的弱分类器可以是不同类的分类器。
4.Bagging和Boosting算法的区别
(1)Bagging的训练集是随机的,各训练集是独立的;而Boosting训练集的选择不是独立的,每一次选择的训练集都依赖于上一次学习的结果;
(2)Bagging的每个预测函数都没有权重;而Boosting根据每一次训练的训练误差得到该次预测函数的权重;
(3)Bagging的各个预测函数可以并行生成;而Boosting只能顺序生成。对于神经网络这样极为耗时的学习方法,Bagging可通过并行训练节省大量时间开销。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




