传统的机器学习分类方法是一个由各种可能的函数构成的空间中寻找一个最接近实际分类函数的分类器,而集成学习的思路是在对新的实例进行分类的时候,把若干个单个分类器集成起来,通过对多个分类器的分类结果进行某种组合来决定最终的分类,以取得比单个分类器更好的性能。如果把单个分类器比作一个决策者的话,集成学习的方法就相当于多个决策者共同进行一项决策。严格意义上来说,集成学习不算是一种机器学习算法,而更像是一种优化手段或者策略,它通常是结合多个简单的弱机器学习算法,去做更可靠的决策。集成模型是一种能在各种的机器学习任务上提高准确率的强有力技术,集成算法往往是很多数据竞赛关键的一步,能够很好地提升算法的性能。拿分类问题举个例,直观的理解,就是单个分类器的分类是可能出错、不可靠的,但是如果多个分类器投票,那可靠度就会高很多。现实生活中,我们经常会通过投票、开会等方式,以做出更加可靠的决策。集成学习就与此类似。集成学习就是有策略地生成一些基础模型,然后有策略地把它们都结合起来以做出最终的决策。集成学习又叫多分类器系统。集成学习是机器学习中一个非常重要且热门的分支,是用多个弱分类器构成一个强分类器,其哲学思想是“三个臭皮匠赛过诸葛亮”。一般的弱分类器可以由决策树、神经网络、贝叶斯分类器、K-近邻等构成。
集成学习是一种新的机器学习范式,它使用多个学习器来解决同一个问题,从而提高整体分类器的泛化能力,因此从20世纪90年代开始,对集成学习的理论和算法的研究成为机器学习领域的一个热点。1988年Kearns和Valiant指出,在PAC学习模型中,若存在一个多项式级的学习算法来识别一组概念,并且识别正确率很高,那么该学习算法是强可学习的;而如果学习算法识别一组概念的正确率仅比随机猜测略好,那么该学习算法是弱可学习的。随后提出了弱学习算法与强学习算法的等价性问题,即是否可以将弱学习算法提升成强学习算法。如果两者等价,那么在学习概念时,只需找到一个比随机猜测略好的弱学习算法,就可以将其提升为强学习算法,而不必直接去寻找通常情况下很难获得的强学习算法。1990年,Schapire通过一个构造性方法对该问题作出了肯定的证明:如果一个概念是弱可学习的,充要条件是它是强可学习的,即多个弱学习器可以集成为一个强学习器。集成机器学习的理论基础由此奠定。
由于集成学习技术可以显著地提高学习系统的泛化能力,因此早在1997年,国际机器学习界的权威就将集成学习列为机器学习四大研究方向之首。而在今天,随着集成学习技术在行星探测、地震波分析、Web信息过滤、生物特征识别、计算机辅助医疗诊断等众多领域的广泛应用,集成学习仍然是机器学习中最热门的研究领域之一。
在机器学习领域,最早的集成学习方法是Bayesian。在此之后,集成学习的研究才逐渐引起了人们的关注。狭义地说,集成学习是指利用多个同质的学习器来对同一个问题进行学习,这里的“同质”是指所使用的学习器属于同一种类型,例如所有的学习器都是决策树、都是神经网络,等等。广义地来说,只要是使用多个学习器来解决问题,就是集成学习[26][27]。在集成学习的早期研究中,狭义定义采用得比较多,而随着该领域的发展,越来越多的学者倾向于接受广义定义。采用广义定义有一个很大的好处,就是以往存在的很多名称上不同、但本质上很接近的分支,例如多分类器系统一、多专家混合、基于委员会的学习等,都统一地归属到集成学习之下。所以在广义的情况下,集成学习已经成为一个包含内容相当多的、比较大的研究领域[28]。
1.集成学习的构成
大致上来说,集成学习的构成方法可以分为四种:
(1)输入变量集重构法。这种构成方法,用于集成的每个算法的输入变量是原变量集的一个子集。这种方法比较适用于输入变量集高度冗余的时候,否则的话,选取一个属性子集,会影响单个算法的性能,最终影响集成的结果。
(2)输出变量集重构法。这种构成方法,主要是通过改变输出变量集,将多分类问题转换为二分类问题来解决。
(3)样本集重新抽样法。在这种构成方法中,用于集成的每个算法所对应的训练数据都是原来训练数据的一个子集。目前的大部分研究主要集中在使用这种构成方法来集成学习,例如Bagging、Boosting等。样本集重新抽样法对于不稳定的算法来说,能够取得很好的效果。不稳定的算法指的是当训练数据发生很小变化的时候,结果就能产生很大变化的算法。如神经网络、决策树。但是对于稳定的算法来说,效果不是很好。
(4)参数选择法。对于许多算法如神经网络、遗传算法来说,在算法应用的开始首先要解决的就是算法参数的选择问题。而且,由于这些算法操作过程的解释性很差,对于算法参数的选择没有确定的规则可依。在实际应用中,就需要操作者根据自己的经验进行选择。在这样的情况下,不同的参数选择,最终的结果可能会有很大的区别,具有很大的不稳定性。
2.集成学习的作用(https://www.xing528.com)
集成学习的基本思想是用多个模型解决方案来解决同一个问题,集成学习模型的一般框架见图5-22所示。
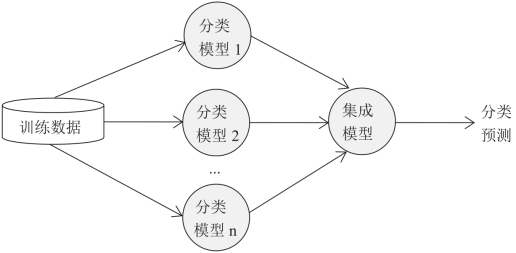
图5-22 集成学习模型一般框架
集成学习模型的作用主要体现在以下四个方面:
(1)提高预测结果的准确性。机器学习的一个重要目标就是对新的测试样本尽可能给出最精确的估计。构造单个高精度的学习器是一件相当困难的事情,然而产生若干个只比随机猜想略好的学习器却很容易。研究者们在应用研究中发现,将多个学习器进行集成后得到的预测精度明显高于单个学习器的精度,甚至比单个最好的学习器的精度更高。集成模型H的分类错误率定义为:

其中,T表示单个模型的数量,p表示单个模型的分类错误率。当T=5,p=0.1时,ErrorH<0.1,显然,当单个模型相互独立时,集成学习模型能够大幅度提升模型的预测精度。
(2)提高预测结果的稳定性。有些学习算法单一的预测结果时好时坏,不具有稳定性,不能一直保持高精度的预测。就拿全球地震预测系统来说,一个模型对于某一个地区的地震可能预测得很好。但是,对于其他地区,可能别的模型会预测得比较好。通过模型的集成,可以在全球范围内以较高的概率普遍取得很好的结果。
(3)解决过适应问题。在对已知的数据集合进行学习的时候,我们常常选择适应度值最好的一个模型作为最后的结果。也许我们选择的模型能够很好地解释训练数据集合,但是却不能很好地解释测试数据或者其他数据,也就是说这个模型过于精细地刻画了训练数据,对于测试数据或者其他新的数据泛化能力不强,这种现象就称为过适应。为了解决过适应问题,按照集成学习的思想,可以选择多个模型作为结果,对于每个模型赋予相应的权重,从而集合生成合适的结果,提高预测精度。
(4)改进参数选择。对于一些算法而言,如神经网络、遗传算法,在解决实际问题的时候,需要选择操作参数。但是这些操作参数的选取没有确定性的规则可以依据,只能凭借经验来选取,对于非专业的一般操作人员会有一定的难度。而且参数选择不同,结果会有很大的差异。通过建立多个不同操作参数的模型,可以解决选取参数的难题,同时将不同模型的结果按照一定的方式集成就可以生成我们想要的结果。
将多个单个模型组合成集成模型的简单策略主要包括:多数投票方法、平均值方法和加权平均方法等;而复杂的策略可以是:将单个基模型的输出当作输入,将数据真实标签当作输出从而训练一个新的模型。简单策略的集成学习模型算法主要有:Bagging、Boosting,而复杂策略的集成学习模型主要有Stacking,下面分别进行概述。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




