支持向量机在大数据挖掘中的应用

分类作为数据挖掘领域中一项非常重要的任务，目前在商业上应用最多。而分类的目的则是学会一个分类函数或分类模型（或者叫作分类器），该模型能把数据库中的数据项映射到给定类别中的某一个，从而可以用于预测未知类别。

本文将要介绍的支持向量机（Support Vector Machine，简称SVM）算法便是一种分类方法。所谓支持向量机，分为两个部分：支持向量（简单来说，就是支持或支撑平面上把两类类别划分开来的超平面上的向量点）和机（Machine，机器，具体指一个算法）。在机器学习领域，常把一些算法看作是一个机器，如分类机（当然，也叫作分类器），而支持向量机本身便是一种监督式学习的方法，它广泛地应用于统计分类以及回归分析中。支持向量机是Corinna Cortes和Vapnik等学者于1995年首先提出的，它在解决小样本、非线性及高维模式识别中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中。在机器学习中，支持向量机（SVM，还支持矢量网络）是与相关的学习算法有关的监督学习模型，可以分析数据、识别模式，用于分类和回归分析。

1.支持向量机基本思想

支持向量机可以理解为“使用了支持向量的算法”^[17]。支持向量机是一种基于分类边界的机器学习方法，最初是针对线性可分情况下的二分类问题而提出来的，所谓线性可分是指原始数据可以用一条直线（如果数据是二维的）或者一个超平面（也叫决策面）来进行分类。支持向量机是定义在特征空间上的间隔最大分类器，它的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，或等价于正则化的损失函数的最小化问题^[18]。支持向量机分类算法的目标是通过训练，找到这些分类之间的边界（如果是直线或超平面，称为线性可分；如果是曲线或曲面，则称为非线性可分）；对于多维数据，可以将它们视为n维空间中的点，而分类边界就是n维空间中的面，称之为超平面。线性分类器使用一条直线或一个超平面进行分类，而非线性分类器则使用超曲面进行分类，通常我们需要找到一个线性可分的分类器。支持向量机通过核函数的方法将低维数据映射到高维空间，并使得在高维空间中的数据是线性可分的，从而能够处理低维空间中线性不可分的情况。

支持向量机通过使用最大间隔来确定最优的划分超平面，使期望泛化误差最小化，以获得良好的泛化能力。所谓最小化泛化误差是指当新的样本（类别未知的数据）进行分类时，基于学习所得的分类器（超平面）使得我们对新数据所属分类的预测错误的概率被最小化。接下来我们以例子来说明最大间隔。

（1）线性可分的二分类问题和间隔最大化。线性可分的二分类问题见图5-12（a），（b），（c）所示。

图5-12

图5-12中的（a）是已有的原始数据，红色（左侧）和蓝色（右侧）分别代表两个不同的类别。数据显然是线性可分的，即可以找到一条直线将这两类数据分开，但是将两类数据点分开的直线显然不止一条。上图的（b）和（c）分别给出了A、B两种不同的分类方案，其中黑色实线为分界线，称为“超平面”。每个超平面对应一个线性分类器。虽然从分类结果上看，分类器A和分类器B的效果是相同的。但是它们的性能是有差距的，见图5-13所示。在“超平面”不变的情况下，又添加了一个红点（箭头指向的那个点）。可以看到，分类器A依然能很好地分类结果，而分类器B则出现了分类错误。显然分类器A的“超平面”放置的位置优于分类器B的“超平面”放置的位置，支持向量机算法也是这么认为的，它的依据就是分类器A的分类间隔比分类器B的分类间隔大。这里涉及第一个支持向量机独有的概念“分类间隔”。在保证超平面方向不变且不会出现错分样本的情况下移动决策面，会在原来的决策面两侧找到两个极限位置（越过该位置就会产生错分现象），如虚线所示。虚线的位置由超平面的方向和距离和原超平面最近的几个样本的位置决定。而这两条平行虚线正中间的分界线就是在保持当前超平面方向不变的前提下的最优超平面。两条虚线之间的垂直距离就是这个最优超平面对应的分类间隔。显然每一个可能把数据集正确分开的方向都有一个最优超平面（有些方向无论如何移动超平面的位置也不可能将两类样本完全分开），而不同方向的最优超平面的分类间隔通常是不同的，那个具有“最大间隔”的超平面就是支持向量机要寻找的最优解。而这个真正的最优解对应的两侧虚线所穿过的样本点，就是支持向量机中的支持样本点，称为“支持向量”。

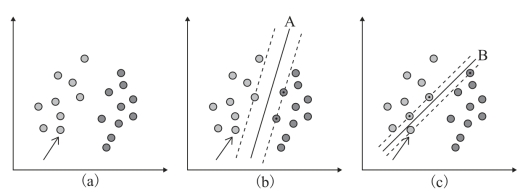
图5-13

（2）支持向量机建模。求解这个“超平面”的过程，就是最优化^[19]。一个最优化问题通常有两个基本的因素：①目标函数，也就是你希望什么东西的什么指标达到最好；②优化对象，你期望通过改变哪些因素来使你的目标函数达到最优。在线性SVM算法中，目标函数显然就是那个“分类间隔”，而优化对象则是超平面。所以要对SVM问题进行数学建模，首先要对上述两个对象（“分类间隔”和“超平面”）进行数学描述。按照一般的思维习惯，我们先描述超平面。数学建模的时候，先在二维空间建模，然后再推广到多维。

①超平面方程。我们都知道二维空间下一条直线的方程可以表示为如下形式：

现在，我们对上述直线方程做一个改变，将让x1替换x，x2替换y，则有：

移项得：

将上述方程向量化得：

进一步向量化，用ω列向量和x列向量和标量γ进一步向量化得：

其中，向量ω和x分别为：

这里ω1＝a，ω2＝-1。我们都知道，最初的那个直线方程：y＝ax＋b中a和b的几何意义，a表示直线的斜率，b表示截距，a决定了直线与x轴正方向的夹角，b决定了直线与y轴交点位置。那么向量化后的直线的ω和γ的几何意义是什么呢？

现在假设：

可得：

在坐标轴上画出直线和向量ω，见图5-14所示。

图5-14　直线和向量ω的关系

蓝色的线（坐标轴下面的线）代表向量ω，红色的线（坐标轴上面的线）代表直线y。我们可以看到向量ω和直线的关系为垂直关系。这说明了向量ω也控制这直线的方向，只不过是与这个直线的方向是垂直的。标量γ的作用也没有变，依然决定了直线的截距。此时，我们称ω为直线的法向量。

二维空间的直线方程已经推导完成，将其推广到n维空间，就变成了超平面方程（一个超平面，在二维空间的例子就是一个直线）但是它的公式没变，依然是：

不同之处在于：

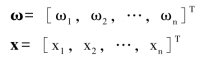
公式（5.32）即为超平面方程。

②分类间隔方程。分类间隔见图5-15所示。我们已经知道间隔的大小实际上就是支持向量对应的样本点到决策面的距离的二倍。那么图中的距离d我们怎么求？我们高中都学过，点到直线的距离公式如下：

公式中的直线方程为Ax＋By＋C＝0，点P的坐标为（x0，y0）。

现在，将直线方程扩展到多维，求得我们现在的超平面方程，对公式进行如下变形：

公式（5.34）中的d就是其中‖ω‖表示ω的二范数，即求所有元素的平方和，然后再开方。比如对于二维平面，则有：

那么，则有：

我们目的是为了找出一个分类效果好的超平面作为分类器。分类器的好坏的评定依据是分类间隔W＝2d的大小，即分类间隔W越大，我们认为这个超平面的分类效果越好。此时，求解超平面的问题就变成了求解分类间隔W最大化的问题。W的最大化也就是d的最大化。

图5-15　分类间隔方程

③约束条件。看起来，我们已经顺利获得了目标函数的数学形式。但是为了求解W的最大值。我们不得不面对如下问题：

我们如何判断超平面是否将样本点正确分类？

我们知道要求距离d的最大值，我们首先需要找到支持向量上的点，怎么在众多的点中选出支持向量上的点呢？

上述我们需要面对的问题就是约束条件，也就是说我们优化的变量d的取值范围受到了限制和约束。事实上约束条件一直是最优化问题里最让人头疼的东西。但既然我们已经知道了这些约束条件确实存在，就不得不用数学语言对它们进行描述。但SVM算法通过一些巧妙的小技巧，将这些约束条件融合到一个不等式里面。

这个二维平面上有两种点，我们分别对它们进行标记：红颜色的圆点标记为1，我们人为规定其为正样本；蓝颜色的五角星标记为-1，我们人为规定其为负样本。

对每个样本点xi加上一个类别标签yi：

如果我们的超平面方程能够完全正确地对上图的样本点进行分类，就会满足下面的方程：

如果我们要求再高一点，假设超平面正好处于间隔区域的中轴线上，并且相应的支持向量对应的样本点到超平面的距离为d，那么公式进一步写成：

上述公式的解释就是，对于所有分类标签为1和-1的样本点，它们到直线的距离都大于等于d（支持向量上的样本点到超平面的距离）。公式两边都除以d，就可以得到：

因为‖ω‖和d都是标量，所以上述公式的两个矢量，依然描述一条直线的法向量和截距。

上述两个公式，都是描述一条直线，数学模型代表的意义是一样的。现在，让我们对ωd和γd重新起个名字，就叫它们ω和γ。因此，我们就可以说：对于存在分类间隔的两类样本点，我们一定可以找到一些超平面，使其对于所有的样本点均满足下面的条件：

上述方程即给出了SVM最优化问题的约束条件。这时候，可能有人会问了，为什么标记为1和-1呢？因为这样标记方便我们将上述方程变成如下形式：

正是因为标签为1和-1，才方便我们将约束条件变成一个约束方程，从而方便我们的计算。

④线性SVM优化问题基本描述。我们用公式（5.34）来求距离d，也就是用支持向量上的样本点求解d的最大化，而对于支持向量上的样本点满足：｜ωT xi＋γ｜＝1，因此，公式（5.34）可以进一步简化为：(www.xing528.com)

求d的最大化，也即求‖ω‖的最小化，可等效于：min1/2‖ω‖2，为了在进行优化的过程中对目标函数求导时方便，我们将最终的目标函数和约束条件放在一起进行描述为：

其中，n是样本点的总个数，缩写s.t.表示“subject to”，是“服从某条件”的意思。公式（5.37）描述的是一个典型的不等式约束条件下的二次型函数优化问题，同时也是支持向量机的基本数学模型。

⑤求解准备。我们已经得到支持向量机的基本数学模型，接下来的问题就是如何根据数学模型，求得我们想要的最优解。在学习求解方法之前，首先就是要保证目标函数必须是凸函数。要理解凸函数，我们还要先明确另一个概念“凸集”在凸几何中，凸集（Convex Set）是在凸组合下闭合的放射空间的子集，见图5-16所示。

图5-16　凸集

图5-16中左右两个图都是一个集合。如果集合中任意2个元素连线上的点也在集合中，那么这个集合就是凸集。显然，上图中的左图是一个凸集，上图中的右图是一个非凸集。凸函数的定义也是如此，其几何意义表示为函数任意两点连线上的值大于对应自变量处的函数值。设函数f为定义在某个区间L上的函数，若对L上的任意两点x1，x2和任意的实数λ，λ属于（0，1），总有：

则函数f称为L上的凸函数，当且仅当在函数图像上方的点集为一个凸集。在学习求解最优化问题之前，我们还要学习拉格朗日函数和KKT条件。

⑥拉格朗日函数。首先，我们先要从宏观的视野上了解一下拉格朗日对偶问题出现的原因和背景。如果能够构造一个函数，使得该函数在可行解区域内与原目标函数完全一致，而在可行解区域外的数值非常大，甚至是无穷大，那么这个没有约束条件的新目标函数的优化问题就与原来有约束条件的原始目标函数的优化问题是等价的问题。这就是使用拉格朗日方程的目的，它将约束条件放到目标函数中，从而将有约束优化问题转换为无约束优化问题。

随后，人们又发现，使用拉格朗日获得的函数，使用求导的方法求解依然困难。进而，需要对问题再进行一次转换，即使用一个数学技巧“拉格朗日对偶”。所以，显而易见的是，我们在拉格朗日优化我们的问题这个道路上，需要进行下面两个步骤：

第一步：将有约束的原始目标函数转换为无约束的新构造的拉格朗日目标函数。

第二步：使用拉格朗日对偶性，将不易求解的优化问题转化为易求解的优化。

下面进行第一步：将有约束的原始目标函数转换为无约束的新构造的拉格朗日目标函数，公式变形如下：

其中ai是拉格朗日乘子，ai大于等于0，是我们构造新目标函数时引入的系数变量，现在我们令：

当样本点不满足约束条件时，即在可行解区域外：

此时，我们将ai设置为正无穷，此时θ（ω）显然也是正无穷。当样本点满足约束条件时，即在可行解区域内：Yi（ωT xi＋b）≥1。

此时，显然θ（ω）为原目标函数本身。我们将上述两种情况结合一下，就得到了新的目标函数：

现在，我们的问题变成了求新目标函数的最小值，即：

这里用p*表示这个问题的最优值，且和最初的问题是等价的。接下来，我们进行第二步：将不易求解的优化问题转化为易求解的优化。我们看一下我们的新目标函数，先求最大值，再求最小值。这样的话，我们首先就要面对带有需要求解的参数ω和b的方程，而ai又是不等式约束，这个求解过程不好做。所以，我们需要使用拉格朗日函数对偶性，将最小和最大的位置交换一下，这样就变成了：

交换以后的新问题是原始问题的对偶问题，这个新问题的最优值用d*来表示。而且d*≤p*。我们关心的是d＝p的时候，这才是我们要的解。需要什么条件才能让d＝p呢？

首先必须满足这个优化问题是凸优化问题，其次需要满足KKT条件。

凸优化问题的定义是：求取最小值的目标函数为凸函数的一类优化问题。目标函数是凸函数我们已经知道，这个优化问题又是求最小值。所以我们的最优化问题就是凸优化问题。接下来，就是探讨是否满足KKT条件了。

⑦KKT条件。我们已经使用拉格朗日函数对我们的目标函数进行了处理，生成了一个新的目标函数。通过一些条件，可以求出最优值的必要条件，这个条件就是接下来要说的KKT条件。一个最优化模型能够表示成下列标准形式：

KKT条件的全称是Karush-Kuhn-Tucker条件，KKT条件是说最优值条件必须满足以下条件：

条件一：经过拉格朗日函数处理之后的新目标函数L（ω，b，α）对x求导为零；

条件二：h（x）＝0；

条件三：a*g（x）＝0；

对于我们的优化问题：

现在，凸优化问题和KKT条件都满足了，问题转换成了对偶问题。而求解这个对偶学习问题，可以分为三个步骤：首先要让L（ω，b，a）关于ω和b最小化，然后求对a的极大值，最后利用SMO算法求解对偶问题中的拉格朗日乘子。现在，我们继续推导。

⑧对偶问题求解。

第一步：

根据上述推导知：

首先固定a，要让L（ω，b，a）关于ω和b最小化，我们分别对ω和b求偏导数，令其等于0，即：

将上述结果代回L（ω，b，a）得到：

从上面的最后一个式子，我们可以看出，此时的L（ω，b，α）函数只含有一个变量，即ai。

第二步：

现在内侧的最小值求解完成，我们求解外侧的最大值，从上面的式子得到：

现在我们的优化问题变成了公式（5.46）。对于这个问题，我们有更高效的优化算法，即序列最小优化（SMO）算法。我们通过这个优化算法能得到a，再根据a，我们就可以求解出ω和b，进而求得我们最初的目的：找到超平面，即“决策平面”。限于篇幅问题，关于SMO算法的求解过程，参考脚注文献^[20]。

⑨核函数和核方法。支持向量机模型的一个独特的特性是可以通过核方法来处理线性不可分的数据，这也是支持向量机的原问题转换为对偶问题所带来的一个优点。现实中很多数据都是线性不可分的，核方法的基本原理是把原坐标系里线性不可分的数据使用核函数映射到另一个高维空间，尽量使得数据在新的空间里线性可分。要在支持向量机中使用核函数，只需要将对偶问题中目标函数的内积项替换成核函数。常用的核函数见表5-12所示。

表5-12　常用的核函数

2.支持向量机的特点及应用

SVM有如下几个主要特点：

（1）非线性映射是SVM方法的理论基础，SVM利用核函数将非线性可分数据映射到高维空间。

（2）对特征空间划分的最优超平面是SVM的目标，最大化分类边际的思想是SVM方法的核心。

（3）支持向量是SVM的训练结果，在SVM分类决策中起决定作用的是少量的支持向量，并且受非支持向量的影响小，因此泛化能力较好。

（4）SVM是一种有坚实理论基础的新颖的小样本学习方法。它基本上不涉及概率测度及大数定律等，因此不同于现有的统计方法。从本质上看，它避开了从归纳到演绎的传统过程，实现了高效的从训练样本到预报样本的“转导推理”，大大简化了通常的分类和回归等问题。

（5）SVM的最终决策函数只由少数的支持向量所确定，计算的复杂性取决于支持向量的数目，而不是样本空间的维数，这在某种意义上避免了维数灾难。

（6）少数支持向量决定了最终结果，这不但可以帮助我们抓住关键样本、剔除大量冗余样本，而且注定了该方法不但算法简单，而且具有较好的鲁棒性。这种鲁棒性主要体现在：

①增、删非支持向量样本对模型没有影响；

②支持向量样本集具有一定的鲁棒性；

③有些成功的应用中，SVM方法对核的选取不敏感。

两个不足：

（1）SVM算法对大规模训练样本难以实施。由于SVM是借助二次规划来求解支持向量，而求解二次规划将涉及m阶矩阵的计算（m为样本的个数），当m数目很大时该矩阵的存储和计算将耗费大量的机器内存和运算时间。针对以上问题的主要改进有：J.Platt的SMO算法、T.Joachims的SVM、C.J.C.Burges等的PCGC、张学工的CSVM以及O.L.Mangasarian等的SOR算法。

（2）用SVM解决多分类问题存在困难。经典的支持向量机算法只给出了二类分类的算法，而在数据挖掘的实际应用中，一般要解决多类的分类问题。可以通过多个二分类支持向量机的组合来解决。主要有：一对多组合模式、一对一组合模式和SVM决策树；再就是通过构造多个分类器的组合来解决。主要原理是克服SVM固有的缺点，结合其他算法的优势，解决多类问题的分类精度。如与粗糙集理论结合形成一种优势互补的多类问题的组合分类器。

支持向量机主要应用在模式识别领域中的文本识别、文本分类、人脸识别等问题中，同时也应用到许多的工程技术和信息过滤等方面。