服刑人员再犯罪预测：K近邻分类

K近邻（K-Nearest Neighbor，KNN）算法是1968年由Cover和Hart提出的一种经典的、简单的有监督分类算法之一。

1.KNN算法原理

KNN算法根据距离函数计算待分类样本X和训练集中每个训练样本间的距离，找到与待分类样本X距离最小的K个训练样本作为X的K个近邻，最后根据这K个近邻样本的类别进行投票来确定待分类样本X的类别，也即以X的K个近邻中的大多数样本所属的类别作为待分类样本X的类别。如果要输出待分类样本X属于各类的概率，可以通过样本X属于各类的数量分布在进行估计。

（1）KNN算法步骤。

①确定K的大小和距离计算的方法；

②计算待分类样本X与训练集中每个训练样本的距离；

③圈定距离最近的K个训练样本作为待分类样本X的近邻；

④统计K个最近邻样本中每个类别出现的次数；

⑤选择出现频率最大的类别作为待分类样本X的类别。

（2）K值的选择。在KNN算法中，不同的K值选择对最终分类结果会产生影响。在图5-10中，当K＝3和K＝6时，同一个预测样本会被分类到不同的类别。

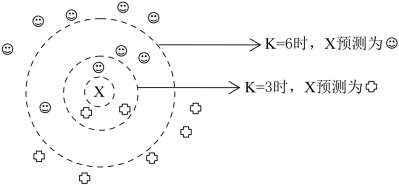
图5-10　不同的K值预测结果的影响

如果K太小，预测目标容易产生变动性；如果K值太大，KNN分类器可能会误分类待分类样本，因为最近邻列表总可能包含远离其近邻的数据点。一般而言，从K＝1开始，随着K值的逐渐增大，KNN算法的分类效果会逐渐提升；在增大到某个值后，随着K的进一步增大，KNN算法的分类效果会逐渐下降；当K增大到训练样本数量相等时，KNN算法对每一个待分类样本的预测结果都会相同。对于一个具体的应用问题，确定最优的K是比较困难的，现实中，可以通过计算不同的K值后的模型分类的错误率来选择，可以选择产生最小错误率的K值。一般而言，训练集越大，K值越大^[14]。

（3）距离函数的选择。计算待分类样本X与训练集中的每个训练样本之间的距离，一般定义一个距离函数d（x，y）需要满足如下准则：

①d（x，x）＝0

②d（x，y）≥0

③d（x，y）＝d（y，x）

④d（x，z）＋d（z，y）≥d（x，y）

距离计算公式分为连续型特征值计算方法和离散型特征值计算方法，公式分别如下：

①连续型特征值的相似度度量方法。闵可夫斯基距离是衡量数值点之间距离的一种常见的方法，假设数值点X和Y的坐标分别为X＝（x1，x2，…，xn）和Y＝（y1，y2，…，yn），则闵可夫斯基距离公式定义为：

多维空间中两个样本的相似度可以使用余弦相似度来度量，它通过两个样本之间的夹角余弦值来计算，则余弦相似度公式定义为：

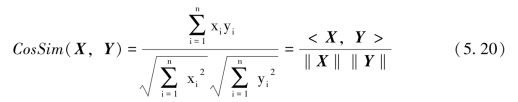
＜X，Y＞表示为两个向量X和Y的内积，余弦相似度越大，代表两个样本向量之间的夹角越小，当两个样本向量的方向完全重合时，余弦相似度为1；当两个样本向量的方向完全相反时，余弦相似度为-1。在度量文本数据的相似度时，通常采用余弦相似度。余弦相似度度量受到向量平移的影响，公式（5.20）中，如果将X平移到X＋1，则余弦值就会改变，怎样才能实现这种平移不变呢？可以使用皮尔逊相关系数，公式定义为：

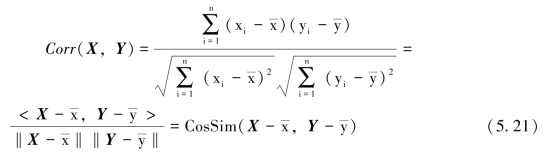
皮尔逊相关系数具有平移不变性和尺度不变性，它计算两个向量的相关性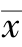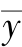，，表示x，y的平均值。

②离散型特征值的相似度度量方法。汉明距离主要用来度量两个等长字符串S1和S2之间的相似度，定义为两个字符串对应位置的不同字符的数量。汉明距离公式定义为：(www.xing528.com)

公式（5.22）中，n为字符串长度，I（.）为指示函数，取1表示某位置两个字符相同。在实际应用汉明距离时，字符串可以为英文单词、信息序列、DNA序列。例如，1011101与1001001之间的汉明距离是2。在一些情况下，某些特定的值相等并不能代表什么，例如，用1表示某个服刑人员发生过某类安全事件，用0表示该服刑人员没有发生过该类安全事件，那么服刑人员发生安全事件的信息就可以用0、1表示成一个序列。考虑到监狱的两个服刑人员如果都没有发生过若干类安全事件，则并不能说明这两个服刑人员相似；但是，如果这两个服刑人员都发生过某类安全事件，则说明这两个服刑人员具有很大的相似性。在这个例子中，序列中等于1所占的权重应该远远大于0的权重，这就引出了杰卡德相似系数。

杰卡德相似系数通常用来比较两个集合之间的相似度。例如，如果将文章看作是词的集合，两篇不同文章的相似度则可以通过两篇文章中共同出现的词的数量和两篇文章的总词的数量来计算。假设A和B是两个集合，则它们之间的杰卡德相似系数定义为：

对应地，我们可求出两个服刑人员发生安全事件的杰卡德相似系数为：

其中，M11表示两个服刑人员都发生过某类安全事件数，M10表示服刑人员A发生过而服刑人员B没有发生过的安全事件数，M01表示服刑人员A没有发生过而服刑人员B发生过的安全事件数。

2.KNN算法应用举例

在表5-11中，每条数据有两个特征及它们所属的类别，待分类样本T＝{18，8}，采用KNN算法求其所属类别^[15]。

表5-11　KNN算法训练集

续表

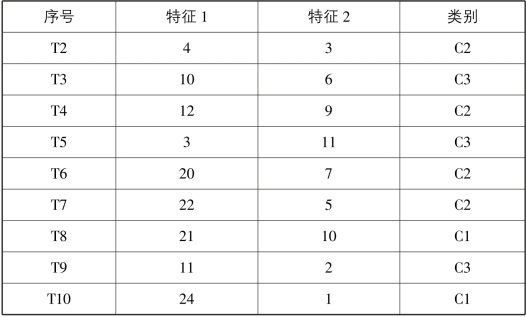
解：本例采用欧几里得距离进行计算，并且设定k＝4。则待分类样本T与各训练样本之间的距离为：

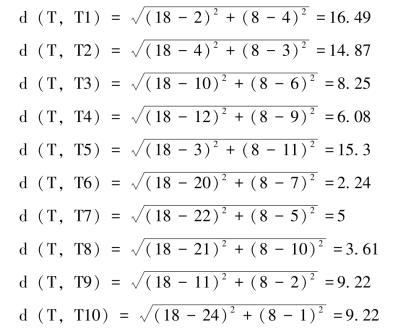
所以，距离T最近的4个样本为：{T6，T8，T7，T4}，它们对应的标签为{C2，C1，C2，C2}，所以T的类别为C2。

3.KNN算法优缺点

（1）优点：

①算法简单，易于理解，易于实现，无需参数估计，无需训练；

②算法精度高，对异常值不敏感（个别噪音数据对结果的影响不是很大）；

③算法适合对稀有事件进行分类；

④算法特别适合于多分类问题（对象具有多个类别标签），KNN要比SVM表现要好。

（2）缺点：

①对测试样本分类时的计算量大，空间开销大，因为对每一个待分类的文本都要计算它到全体已知样本的距离，才能求得它的K个最近邻点。目前常用的解决方法是事先对已知样本点进行剪辑，事先去除对分类作用不大的样本；

②可解释性差，无法给出决策树那样的规则；

③最大的缺点是当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。该算法只计算“最近的”邻居样本，某一类的样本数量很大，那么或者这类样本并不接近目标样本，或者这类样本很靠近目标样本。无论怎样，数量并不能影响运行结果。可以采用权值的方法（和该样本距离小的邻居权值大）来改进；

④消极学习方法。这种学习方式不是根据样本建立一般化的目标函数并确定其参数，而是简单地把训练样本存储起来，直到需要分类新的实例时才分析其与所存储样例的关系，据此确定新实例的目标函数值。也就是说这种学习方式只有到了需要决策时才会利用已有数据进行决策，而在这之前不会经历积极学习所拥有的训练过程。