逻辑回归-大数据挖掘再犯罪预测

1.逻辑回归概述

先前所讲的线性回归主要是用于预测连续的因变量，即根据已知的数据去预测未来的数值。例如用线性回归预测未来的房价。然而在现实世界中，很多因变量不是连续的值而是离散值。例如邮件是否为垃圾邮件、金融交易是否正常，肿瘤是否是良性的、服刑人员是否再犯罪等。这些问题都是一个分类。在分类问题中，结果一般是为0和1，0称为负样本或者是负类，如良性肿瘤、没有再犯罪。1称为正样本或者是正类，如恶性肿瘤、再犯罪。许多人对线性回归都比较熟悉，但知道逻辑回归的人可能就要少得多。逻辑回归又叫Logistic（逻辑斯蒂）回归，是一种广义的线性回归分析模型，常用于数据挖掘、疾病自动诊断、经济预测、风险控制与评估等领域。之所以称为“回归”，是因为它采用了回归分析的思想，然后它是用来预测分类的模型。从大的类别上来说，逻辑回归是一种有监督的统计学习方法，主要用于对数据样本进行分类。在线性回归模型中，输出一般是连续的，例如：y＝f（x）＝β0＋β1 x，对于每一个输入的x，都有一个对应的y输出。模型的定义域和值域都可以是（-∞，＋∞）。但是对于逻辑回归，输入可以是连续的（-∞，＋∞），但输出一般是离散的，即只有有限多个输出值。例如，其值域可以只有两个值{0，1}，这两个值可以表示对样本的某种分类，高/低、患病/健康、阴性/阳性等，这就是最常见的二分类逻辑回归。因此，从整体上来说，通过逻辑回归模型，我们将在整个实数范围上的x映射到了有限个点上，这样就实现了对x的分类。因为每次拿过来一个x，经过逻辑回归分析，就可以将它归入某一类y中。

逻辑回归的因变量可以是二分类的，也可以是多分类的，但是二分类（即输出的类别有两种）的更为常用，也更加容易解释，多分类可以使用某种方法变换成二分类处理。实际中最为常用的就是二分类的逻辑回归，主要应用于预测某种事件类别发生的概率。

逻辑回归模型的适用条件如下：

（1）因变量为二分类的分类变量或某事件的发生率，并且是数值型变量。但是需要注意，重复计数现象指标不适用于逻辑回归。

（2）残差和因变量都要服从二项分布。二项分布对应的是分类变量，所以不是正态分布，进而不是用最小二乘法，而是最大似然法来解决方程估计和检验问题。

（3）自变量和逻辑概率是线性关系。

（4）各观测对象间相互独立。

2.逻辑回归模型

从前面的介绍，我们知道线性回归中预测的因变量y是连续型的，并且可以写成自变量（特征）的线性加权形式：

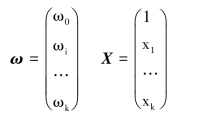
其中，一般在分类模型中用ω表示参数向量，和线性回归中的β具有相同的含义。k为自变量个数（特征的维度数）。现在我们要预测二分类问题，显然线性回归不能提供解决办法，因为线性回归的预测值是连续的实数，而不是离散值。逻辑回归其实仅为在线性回归的基础上，套用了一个逻辑斯蒂（Logistic）函数，将连续型的输出映射到（0，1）之间，则逻辑斯蒂函数定义为：

对应的逻辑斯蒂函数曲线如图5-9所示。当输入的x很大或很小时，该函数的输出值无限接近于1或0。

有了逻辑斯蒂函数，我们就可以将任意实数映射到（0，1）之间，在逻辑回归中，这个输出可以解释为样本属于正类（y＝1）的概率，函数形式为：f（x）＝ωT x，则在逻辑回归模型中，样本xi的类别为正类（y＝1）的概率定义为：(www.xing528.com)

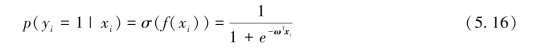
样本xi的类别为负类（y＝-1）的概率为：

在样本xi的类别为负类时，将公式（5.16）和（5.17）合并，可得：

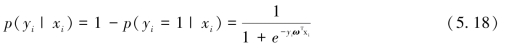
图5-9　逻辑斯蒂函数

3.逻辑回归的优缺点

优点：

（1）速度快，适合二分类问题，预测结果是界于0和1之间的概率。

（2）容易使用和解释，直接看到各个特征的权重。

（3）可以适用于连续型和离散型自变量，能容易地更新模型吸收新的数据。

缺点：

（1）对模型中自变量多重共线性较为敏感，例如两个高度相关自变量同时放入模型，可能导致较弱的一个自变量回归符号不符合预期，符号被扭转。需要利用因子分析或者变量聚类分析等手段来选择代表性的自变量，以减少候选变量之间的相关性。

（2）对数据和场景的适应能力有局限性，不如决策树算法适应性那么强。