基于大数据挖掘的再犯罪预测-FP-Growth算法

众所周知，Apriori算法在产生频繁模式完全集前需要对数据库进行多次扫描，同时产生大量的候选频繁项集，这就使Apriori算法时间和空间复杂度较大。但是Apriori算法有一个很重要的性质：频繁项集的所有非空子集都必须也是频繁的，因此，通过该性质来压缩搜索空间。Apriori算法在挖掘频繁模式^[7]的时候性能往往低下，Jiawei Han提出了FP-Growth算法^[8]。该算法巧妙地将树型结构引入算法中，它采取“分而治之”策略：将提供频繁项集的数据库压缩到一棵频繁模式树（FP-Tree），然后基于大的FP-Tree构造小的FP-Tree。该算法将原始的数据集进行压缩，但仍将原始数据集中的项集及其支持度等进行了存储，数据量比原始数据集大大减少。该算法和Apriori算法最大的不同有两点：

第一，不产生候选集；

第二，只需要两次遍历数据库，大大提高了效率。

FP-Growth算法主要分为FP-Tree的构建和基于FP-Tree递归地挖掘频繁项集两个步骤。

1.FP-Growth算法基本步骤

第一步：按照以下步骤构造FP-Tree：

（1）先定义最小支持度min_sup，然后遍历一遍数据集并计算各特征元素（候选1项集C1）的支持度，过滤掉那些小于最小支持度的特征元素，把剩下的特征元素按支持度从高到低排序，同时将原始数据集做修改，只保留各项集中剩下的高频率特征元素（频繁1项集L1），并且每个项集中特征元素的排列是按元素的频率高低排列的。

（2）第二次扫描，使用频繁1项集L1中的特征元素创建频繁项头表（从上往下降序）以及FP树。创建FP-Tree的根节点，记为T，并且标记为“null”。然后对D中的每个事务Trans执行：

选择Trans中的频繁项，并按照L中次序排序。设Trans排序后的事务项列表记为[p｜P]，其中p是第一个元素，P是剩余元素的列表。调用insert_tree（[p｜P]，T）。该过程执行情况如下：如果T有子女N使得N.item-name＝p.item-name，则将N的计算增加1；否则，创建一个新节点N，并使它的计数设置为1，并链接到它的父节点T，并且通过节点链接结构将其链接到具有相同item_name的节点。如果P非空，则递归调用insert_tree（P，N）。

第二步：根据FP-Tree挖掘频繁项集，该过程实现算法如下：

if（Tree只包含单路径P）then

for路径P中节点的每个组合（记为β）

生成模式B∪α，其支持度support＝β中所有节点的最小支持度；

else for each ai在Tree头部{

生成模式B＝ai∪α，其支持度support＝ai.support；

构造β的条件模式基，然后构造β的条件FP-tree Treeβ；

if Treeβ≠Фthen

调用FP-Growth（Treeβ，β）；}^[9]

2.FP-Growth算法实例

（1）数据集。表5-7为对发票进行统计后，获得的商品购买数据集。

表5-7　商品购买数据集

（2）FP-Growth算法过程。

①对表5-7中的数据集，遍历数据集，计算数据集中每个特征元素的支持度，并按照支持度降序排列，结果见表5-8所示。

表5-8　元素及其支持度列表

②设定支持度阈值为0.6，过滤掉那些小于最小支持度的特征元素，把剩下的特征元素按支持度从高到低排序，同时将原始数据集做修改，只保留各项集中剩下的高频率特征元素（频繁1项集L1），并且每个项集中特征元素的排列是按元素的频率高低排列的，对原始数据集修改见表5-9所示。

表5-9　频繁1项集L1

(www.xing528.com)

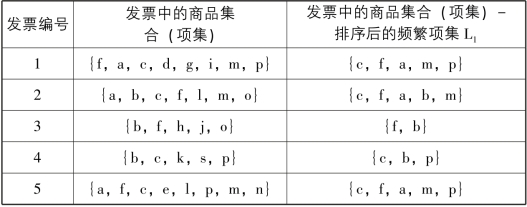
③创建FP-Tree，记为T，构建根节点，标记为“null”，创建频繁项表，将链表列设置为空，从排序好的频繁项集L1中选择第一条商品交易{c，f，a，m，p}插入树T中，因为FP-Tree不存在特征元素，所以如图5-2所示。

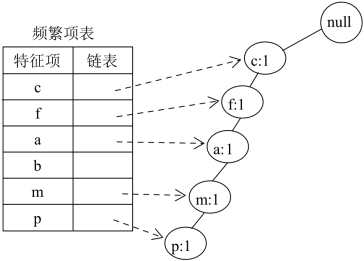
图5-2　插入{c，f，a，m，p}后的树T

向树T中插入第二条商品交易{c，f，a，b，m}，由于该条交易的前缀“cfa”与第一条交易相同，因此，对应的节点可以共用，只需要将对应节点的支持度计数加1即可。而对应的“bm”则需要重新创建节点，并更新频繁项表对应的链接。例如，此时，FP-Tree中有两个“m”节点，需要将它们链接起来，插入第二条交易后的FP-Tree见图5-3所示。

同理，插入第三、四、五条交易后的FP-Tree见图5-4、5-5、5-6所示。

FP-Tree有几个特点：首先，因为很多特征项在树中共享节点，所以其大小通常远远小于原始数据集。其次，对于挖掘频繁项集需要的支持度信息已经在FP-Tree的每一个节点进行了存储。因此，进行频繁项挖掘时，我们可以仅仅利用FP-Tree，从而节省了多次遍历原始数据的步骤。FP-Growth算法优点：对于数据集只进行了两次遍历，时间上快于Apriori算法；FP算法缺点：第一，实现比较困难；第二，需要构建大量的树，空间复杂度的要比Apriori算法高。

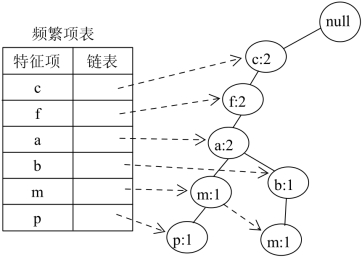
图5-3　插入{c，f，a，b，m}后的树T

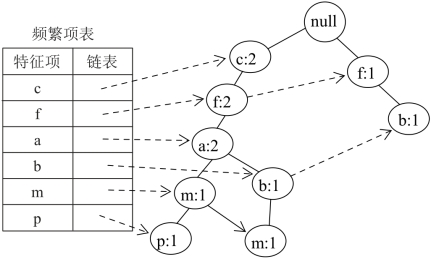
图5-4　插入{f，b}后的树T

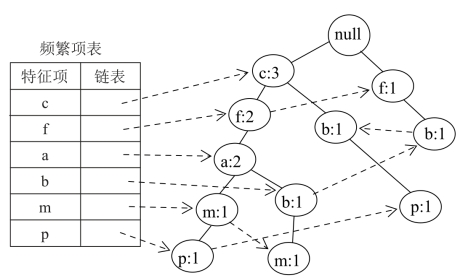
图5-5　插入{c，b，p}后的树T

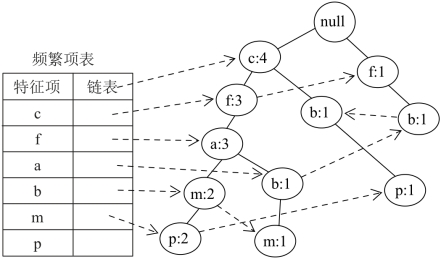
图5-6　插入{c，f，a，m，p}后的树T

④从FP-Tree中挖掘频繁项集分为两步：

第一步：从FP-Tree中获取条件模式库。

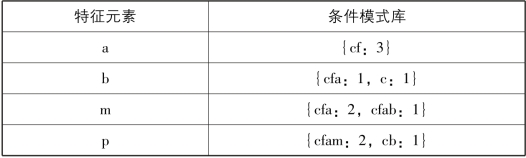
条件模式库：是从原始数据集的FP-Tree中投影出的子数据集，以查找每个特定元素项为结尾的路径集合，每一条路径其实都是一条前缀路径，所以称为条件模式库。简而言之，一条前缀路径就是介于所查找元素项与树根节点之间的所有内容。例如，从图5-6中构造以P为后缀的条件模式库的方法为：顺着频繁项表中P的链表结构依次从FP-Tree中找出两条路径：cfamp和cbp。除去P节点，这两条路径中节点组成了新的项集，项集的支持度设置为对应路径中p的支持度计数，则得到以p为后缀的条件模式库为：{cfam：2，cb：1}。同理，我们可以得到频繁项表中每一个特征元素的条件模式库，如表5-10所示。

表5-10　商品数据的条件模式库

续表

第二步：创建条件FP-Tree：

基于发现的条件模式库，使用和上面相同的建树方法来构建FPTree，直到条件模式库为空集时停止。然后，递归地发现频繁项集、发现条件模式库，以及发现另外的条件FP-Tree。从表5-10可以看出，我们将原始数据划分成对应于某一个特征元素的条件模式库，相当于将一个大的数据集划分成了一些小数据集。例如，对p的条件模式库{cfam：2，cb：1}，首先过滤掉不频繁项后为{c：3}（支持度阈值为0.6，原始数据的项集数为5），则构建的的条件FP-Tree只包含一个根节点和c节点，见图5-7所示。

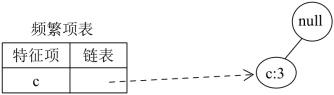
图5-7　p的条件FP-Tree

同理，对m、b、a、f、c的条件模式库进行过滤掉不频繁项后分别为：{cfa：3}、{}、{cf：3}、{c：3}、{}。根据图5-7可以把它们的条件FP-Tree画出来。

基于条件FP-Tree可以挖掘频繁项集，当条件FP-Tree只有一条单独路径或以单独路径作为前缀时，可以直接通过该单独路径中的特征元素进行组合产生频繁项集。例如m的条件FP-Tree只包含一条路径c→f→a，因此，根据该单独路径可以生成频繁项集：{cm：3，fm：3，am：3，cfm：3，cam：3，fam：3，cfam：3}。同理b，a，f，p，c的频繁项集分别为：{}、{ca：3，fa：3，cfa：3}、{cf：3}、{cp：3}、{}。

⑤关联规则的生成。与Apriori算法一样，FP-Growth算法生成的也是频繁项集，而不是关联规则，如果要进一步生成强关联规则，首先需要根据FP-Growth算法生成的频繁项集生成候选的关联规则，然后再使用预先设定好的置信度阈值进行过滤，得到强关联规则。

FP-Growth算法首先通过遍历两次原始数据集，将原始数据集表示成一个压缩的树形数据结构FP-Tree。后续的频繁项集挖掘直接利用FP-Tree，而不再依赖于原始数据集。通常，FP-Tree要比原始数据集小，因此与遍历原始数据集的Apriori算法相比，FP-Growth算法往往能够获得更高的性能。其次，对FP-Tree的挖掘过程也是利用“分而治之”的思想，不断对构造的条件FP-Tree进行递归挖掘来实现。条件FP-Tree比初始的FP-Tree规模进一步缩小，这也是FPGrowth算法性能高效的原因。再次，与Apriori算法相比，FP-Growth算法并没有生成无用的候选项集^[10]。当然，FP-Growth算法也有缺点，该算法采取增长模式的递归策略，虽然避免了无用候选项集的产生，但在挖掘频繁项集的过程中，如果项集的数据量很多，并且由原始数据集得到的FP-Tree的分枝很多，而且分枝长度又很长时，该算法需要构造出数量巨大的条件FP-Tree，不仅浪费时间而且占用大量的空间，挖掘效率不高，而且采用递归算法本身效率也较低^[11]。