1.Apriori算法的基本思想
关联规则的挖掘分为两步:
(1)找出所有频繁项集。这一阶段找出所有满足最小支持度的项集,找出的这些项集称为频繁项集。
(2)生成强关联规则。在上一步产生的频繁项集的基础上生成满足最小置信度的规则,产生的规则称为强关联规则。
强关联规则挖掘所花费的时间主要是在找出频繁项集上,因为找出的频繁项集往往不会很多,利用频繁项集生成规则也就不会花太多的时间,而生成频繁项集需要测试很多的备选项集,如果不加优化,所需的时间是O(2N)。Apriori算法采用了迭代的方法,先对数据集D进行查找,搜索出候选1项集C1及其对应的支持度,剪枝去掉低于最小支持度的1项集,得到频繁1项集L1。然后对剩下的频繁1项集L1进行连接,得到候选的频繁2项集C2,筛选去掉低于最小支持度的候选频繁2项集,得到真正的频繁2项集L2,以此类推,迭代下去,直到无法找到频繁k+1项集为止,对应的频繁k项集的集合Lk即为算法的输出结果。Apriori算法过程中有连接步和剪枝步。
①连接步是自连接,通过Lk-1与自身连接,原则是保证前k-2项相同,并按照字典顺序连接,产生候选项集Ck。
②剪枝步,是使任一频繁项集的所有非空子集也必须是频繁的,从候选项集中过滤不频繁项集,得到频繁的k项集Lk。算法示意图具体见图5-1所示。
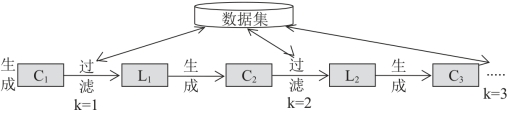
图5-1 Apriori算法示意图
2.Apriori算法性质
Apriori翻译成中文是“先验”,所以,不难想到,先验性质就是整个Apriori的核心。
定理1:先验性质:频繁项集的所有非空子集也一定是频繁的。
说明:这个概念很容易理解了,比如一个项集{I1,I2,I3}是频繁的,那么,说明这三个项同时出现的次数是大于最小支持度计数的,所以,我们可以推知,它的任何非空子集,{I1},{I2,I3}等的支持度也一定比预先定义的阈值要大,故而都是频繁的。
反过来,我们可以换个角度来思考这个问题,如果一个项集I是频繁的,那么给这个项集再加一个项A,则这个新的项集{I∪A}至少不会比I更加频繁,因为加了东西,所以项集中所有项同时出现的次数一定不会增加。进一步思考可以得到这样一个结论:如果项集I是非频繁的,那么无论给它增加什么项,多少项,它都不会变成频繁项集。这种特殊的性质,也叫“反单调性”。我们将这种“反单调性”换个说法,写成下面的定理2。
定理2:反单调性:一个项集,如果有至少一个非空子集是非频繁的,那么这个项集一定是非频繁的。
正是利用了上面的定理1,定理2被设计出来,它通过逐层搜索的模式,由频繁k-1项集生成频繁k项集,从而最终得到全部的频繁项集。可见,Apriori最核心的部件就是怎样通过频繁k-1项集生成频繁k项集。为什么要通过这种方法找频繁k项集呢?通过定理1,2,我们知道:如果一个项集是频繁k项集,那么它的任意非空子集一定是频繁的,所以说,假如现在我们找到了全部的频繁k-1项集,那么频繁k项集则一定是由这些频繁k-1项集组合生成的。可以精简为下面的2个定理。
定理3:任何频繁k项集都是由频繁k-1项集组合生成的。
定理4:频繁k项集的所有k-1项子集一定全部都是频繁k-1项集。
3.Apriori算法步骤
Apriori算法的主要步骤如下:
(1)扫描数据库D中所有数据,产生候选1项集C1;
(2)依据最小支持度,从候选1项集C1中过滤掉非频繁1项集,产生频繁1项集L1;
(3)在k>1的情况下,重复执行步骤(4)、(5)、(6);
(4)由Lk执行连接和剪枝操作,自由产生候选的(k+1)-项集Ck+1;
(5)遍历一次数据集,计算Ck+1中的每一个项集的支持度,依据最小支持度和Apriori算法性质,删除支持度小于min_sup的(k+1)项集后,得到频繁(k+1)项集Lk+1;
(6)如果L≠Ф,则k=k+1,调回第(4)步;否则执行第(7)步;(https://www.xing528.com)
(7)依据最小置信度,对于每个频繁项集L,产生L的所有非空子集,进而产生强关联规则,结束。
4.Apriori算法实例
(1)数据集。表5-2为一个手机评论数据集,该数据集每一列表示对应的词语在一篇评论中是否出现。
表5-2 手机评论数据
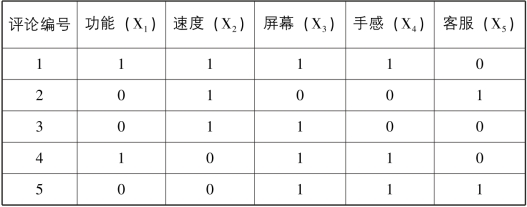
为了便于描述,我们使用特征集合取代特征向量来表示每个样本,集合中的元素为样本中取值为1的所有特征。此时,样本的每一个特征Xi被称为项,每个样本可看做是项的集合,即项集。表5-3为手机评论数据的集合表现形式。
表5-3 手机评论数据的集合表示形式
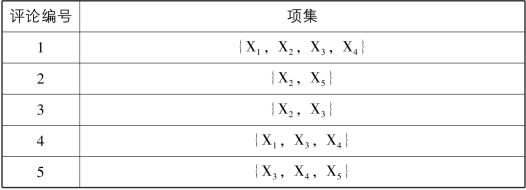
(2)Apriori算法过程
对表5-3进行关联规则挖掘,假设支持度阈值为0.6,置信度阈值为0.5。由于该数据集总共有5条数据,则至少在3条数据中都出现的项集才是频繁项集。
①遍历整个数据集,计算每一个1项集(候选1项集C1)的支持度,见表5-4所示。
表5-4 手机评论数据中候选1项集C1
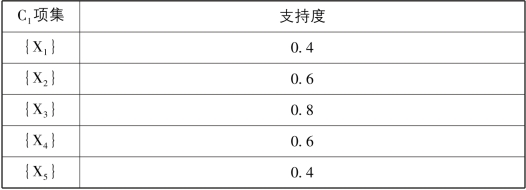
②将C1中支持度小于最小支持度min_sup(本例中为0.6)的项集X1和X5过滤掉,得到1项频繁项集L1={{X2},{X3},{X4}}。
③根据L1生产候选2项集C2,遍历该数据集,得到每一个候选项集的支持度,见表5-5所示。
5-5 手机评论数据中候选2项集C2
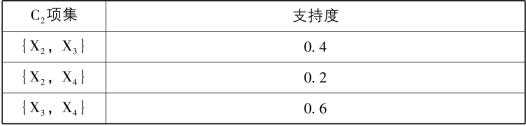
从表5-5可以看出,只有项集{X3,X4}的支持度不小于最小支持度,因此,得到频繁2项集L2={{X3,X4}}。因为L2中只包含一个频繁项集,因此不能再生产C3,L2是最大频繁项集,Apriori算法结束。
④合并L1和L2,我们得到手机评论数据中的频繁项集为:{{X2},{X3},{X4},{X3,X4}}。
⑤由频繁项集产生强关联规则。对L2生成管理规则,并计算这些规则的置信度,见表5-6所示。
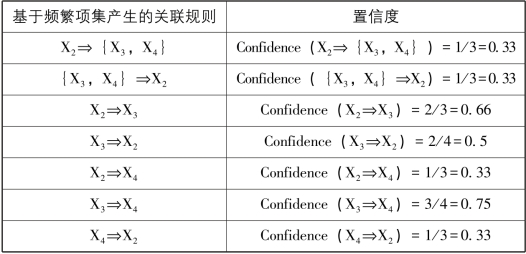
表5-6 基于频繁项集产生的关联规则及其置信度
续表

从表5-6可以看出,规则X2⇒X3,X3⇒X2,X3⇒X4和X4⇒X3的置信度都大于min_conf,因此这四个规则为强关联规则,算法结束。
Apriori算法的应用非常广泛,超市的物品关联摆放、百度文库推荐相关文档、在线电子商务(例如当当、卓越、淘宝等)网站的相关推荐、银行推荐相关联业务等。但是它在运算的过程中会产生大量的候选集,特别是当数据集很大时,数据无法一次性装载入内存,遍历数据集的计算代价成为算法性能的主要瓶颈。而且Apriori算法的每一次迭代过程中均需要遍历数据集,因此在大规模数据集上效率较低。下一节将介绍FP-Growth算法,该算法避免了Apriori算法多次遍历数据集的缺点,一共只需要遍历2次数据集。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




