数值规约：有参数方法与无参数方法

数值规约是指通过选择替代的、较小的数据来减少数据量，包括有参数方法和无参数方法两类。有参数方法是使用一个模型来评估数据，只需存放参数，而不需要存放实际数据，例如：回归和对数线性模型等。而无参数方法则需要存放实际数据，例如：直方图、聚类和抽样^[38]。下面对无参数方法进行介绍。

1.直方图

使用直方图可以近似表示数据的分布，是一种常用的数值规约形式。某个属性的直方图将该属性的数据分布划分为不相交的子集或桶，如果每个桶只代表单个属性值/频率对，则该桶称为单值桶。一般而言，桶用于表示该属性的一个连续区间。例如：某个商品的单价数据（按照四舍五入取整）排序如下：

1，1，5，5，5，5，5，8，8，10，10，10，10，12，14，14，14，15，15，15，15，15，15，18，18，18，18，18，18，18，18，20，20，20，20，20，20，20，21，21，21，21，25，25，25，25，25，28，28，30，30，30.

图4-13为这些数据的频率直方图。

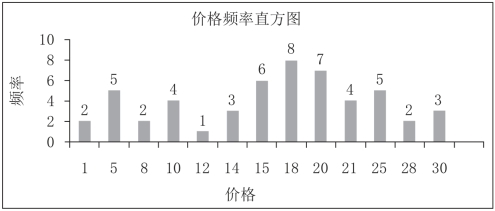
图4-13　使用单值的价格频率直方图

为进一步压缩数据，通常让一个桶代表给定属性的一个连续值域。在图4-14中每个桶代表价格的一个不同的10美元区间。

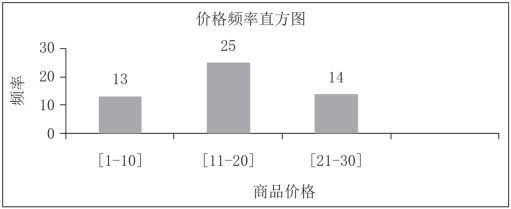
图4-14　商品价格的等宽直方图

2.聚类

聚类技术把数据元组（数据库表中的行）看作对象。它将对象划分为群或簇，使得在一个簇中的对象“相似”，而与其他簇中的对象“相异”。通常，相似性基于距离函数，用对象在空间中的“接近”程度定义。簇的“质量”可以用直径表示，直径是簇中两个对象的最大距离。形心距离是簇质量的另一种度量，它定义为簇中每个对象到簇形心（表示“平均对象”，或簇空间中的平均点）的平均距离。在数值规约中，用数据的簇代表替换实际数据。该技术的有效性依赖于数据的性质。相对于被污染的数据，该技术对能够组织成不同的簇的数据有效得多。

3.抽样

抽样也是一种数据规约技术，因为它允许用较少的随机样本（子集）表示原始数据集。假定原始数据集D包含N个元组，则用于数据规约最常用的对D的抽样方法如下：

（1）s个样本的无放回简单随机抽样（SRSWOR）：从D的N个元组中抽取s个样本（s＜N），其中D中任意元组被抽取的概率均为1/N，即所有元组的抽取是等可能的。

（2）s个样本的有放回简单随机抽样（SRSWR）：该方法类似于SRSWOR，不同之处在于当一个元组从D中抽取后，记录它，然后放回原处。也就是说，一个元组被抽取后，它又被放回D中，以便它可以被再次抽取。

（3）簇抽样：如果D中的元组被分组，放入M个互不相交的“簇”，则可以得到s个簇的简单随机抽样（SRS），其中s＜M。例如，数据库中元组通常一次取一页，这样每页就可以视为一个簇。例如，可以将SRSWOR用于页，得到元组的簇样本，由此得到数据的规约表示。也可以利用其他携带更丰富语义信息的聚类标准。例如，在空间数据库中，我们可以基于不同区域位置上的邻近程度定义簇。

（4）分层抽样：如果D被划分成互不相交的部分，称作“层”，则通过对每一层的SRS就可以得到D的分层抽样。特别是当数据倾斜时，分层抽样可以帮助确保样本的代表性。例如，可以依据罪犯的每个年龄组创建分层，通过SRS得到关于罪犯数据的一个分层抽样。这样，所包含罪犯人数最少的年龄组肯定能够被代表。

采用抽样进行数据规约的优点是，得到样本的花费正比例于样本集的大小s，而不是数据集的大小N。因此，抽样的复杂度可能亚线性（Sublinear）于数据的大小。其他数值规约技术至少需要完全扫描D。对于固定的样本大小，抽样的复杂度仅随数据的维数n线性增加；而在使用其他技术如直方图时，复杂度随n呈指数增长。用于数据规约时，抽样最常用来估计聚集查询的回答。在指定的误差范围内，可以确定（使用中心极限定理）估计一个给定的函数所需的样本大小。样本的大小s相对于N可能非常小。对于规约数据的逐步求精，抽样是一种自然选择。通过简单地增加样本大小，这样的集合可以进一步求精。

【注释】

[1]参见王振武：《大数据挖掘与应用》，清华大学出版社2017年版。

[2]参见张良均等：《Python数据分析与挖掘实战》，机械工业出版社2015年版。

[3]数值型数据的均值可以用公式＜math display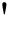＝block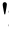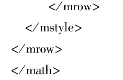＞计算而来，其中xi代表每一个样本属性值。

[4]统计上把一组数据中出现次数最多的变量值叫作众数，用Mo表示，众数是一种位置平均数。众数是在一组数据中，出现次数最多的数据，是一组数据中的原数据，而不是相应的次数。如果数据属于类别数据，则通过直接观察找出频数最多的即为众数，否则可用公式计算。根据计算公式：MO＝ξ-3（ξ-Md）可求众数。其中，式中ξ为样本均值，Md为中数，用皮尔逊公司计算所得众数近似于理论众数，常称为皮尔逊近似众数。众数是皮尔逊（Pearson，K.）最先提出并在生物统计学中使用的，以上是数据出自于离散型随机变量时求众数的方法，对于连续型随机变量ξ，若概率密度函数为f，且f恰有一个最大值，则此最大值称为ξ的众数，有时也把f的极大值称为众数；f有两个以上极大值时，亦称复众数。

[5]参见欧高炎等：《数据科学导引》，高等教育出版社2017年版。

[6]参见张良均等：《Python数据分析与挖掘实战》，机械工业出版社2015年版。

[7]参见欧高炎等：《数据科学导引》，高等教育出版社2017年版。

[8]参见[美]韩家炜等：《数据挖掘概念与技术》，范明等译，机械工业出版社2015年版。

[9]参见马国富、王子贤、马胜利：“基于大数据的服刑人员危险性预测”，载《河北大学学报（自然科学版）》2016年第6期。(www.xing528.com)

[10]马国富、王子贤、马胜利：“基于大数据的服刑人员危险性预测”，载《河北大学学报（自然科学版）》2016年第6期。

[11]参见王茜、张刚景：“实现单敏感属性多样性的微聚集算法”，载《计算机工程与应用》2015年第11期。

[12]童云海等：“隐私保护数据发布中身份保持的匿名方法”，载《软件学报》2010年第4期。

[13]乔宏明、梁奂：“运营商面向大数据应用的数据脱敏方法探讨”，载《移动通信》2015年第13期。

[14]李林：“基于K-匿名技术的隐私保护研究”，杭州电子科技大学2013年硕士学位论文。

[15]李林：“基于K-匿名技术的隐私保护研究”，杭州电子科技大学2013年硕士学位论文。

[16]童云海等：“隐私保护数据发布中身份保持的匿名方法”，载《软件学报》2010年第4期。

[17]Latanya Sweeney，“K-anonymity：A Model for Protecting Privacy”，International Journal of Uncertainty Fuzzinessand Knowledge-Based Systems，pp.557～570.

[18]Dwork C，Mcsherry F，Nissim K，“Calibrating Noise to Sensitivity in Private Data Analysis”，Theory ofCryptography，pp.265～284.

[19]Mcsherry F，Talwar K，“Mechanism Design via Differential Privacy”，IEEE Symposium on Foundations ofComputer Science IEEE Computer Society，pp.94～103.

[20]Xi He，A.Machanavajjhala，B.Ding，“Blowfish Privacy：Tuning Privacy-utility Trade-offs Using Policies”，pp.1447～1458.

[21]黄灿：“数据发布中隐私保护关键技术的研究”，南京航空航天大学2010年硕士学位论文。

[22]黄灿：“数据发布中隐私保护关键技术的研究”，南京航空航天大学2010年硕士学位论文。

[23]乔宏明、梁奂：“运营商面向大数据应用的数据脱敏方法探讨”，载《移动通信》2015年第13期。

[24]陈天莹、陈剑锋：“大数据环境下的智能数据脱敏系统”，载《通信技术》2016年第7期。

[25]所谓量纲，简单地说，就是单位。有一些情况下，描述一个量值，必须使用单位。比如一个物体的长度，那就必须用米或者厘米等表示长度的单位，否则告诉你一个东西长度是100，那跟没说一样，100米还是100厘米？与之相对应的，有一些量值实际上是没有单位的。比如一个物体的质量是另一个物体的10%，这个10%就是无量纲的。综上所述，简单来说，物理现象或物理量的度量就叫作量纲。

[26]参见欧高炎等：《数据科学导引》，高等教育出版社2017年版。

[27]Dougherty J，Kohavi R，SahamiM，“Supervised and Unsupervised Discretization of Continuous Features”，Twelfth International Conference on Machine Learning，pp.194～202.

[28]喻小光、陈维斌、陈荣鑫：“一种数据规约的近似挖掘方法的实现”，载《华侨大学学报（自然科学版）》2008年第3期。

[29]参见朝乐门：《数据科学》，清华大学出版社2016年版。

[30]参见陈封能、斯坦巴赫、库玛尔：《数据挖掘导论（完整版）》，人民邮电出版社2011年版。

[31]Forever-守望：“机器学习中的维数灾难”，https：//blog.csdn.net/zbc1090549839/article/details/38929215，最后访问日期：2018年4月12日。

[32]许明旺、施润身：“维规约技术综述”，载《计算机应用》2006年第10期。

[33]参见王振武：《大数据挖掘与应用》，清华大学出版社2017年版。

[34]刘振焘等：“语音情感特征提取及其降维方法综述”，载《计算机学报》2017年第40卷。

[35]Zhang L，et al，“Feature Selection for Fast Speech Emotion Recognition”，International Conference on Multimedia，2009，pp.753～756.

[36]Huang RS，“Information Technology in an Improved Supervised Locally Linear Embedding for Recognizing Speech Emotion”，Advanced Materials Research，pp.375～378.

[37]Yu Q，Li Y，Jia P，“Speech Emotion Recognition Using Supervised Manifold Learning Based on All-class and Pairwise-class Feature Extraction”，C onference Anthology，IEEE，pp.1～5.

[38]参见[美]韩家炜等：《数据挖掘概念与技术》，范明等译，机械工业出版社2015年版。