大数据挖掘算法预测服刑人员再犯罪

1.隐私数据脱敏算法

将数据开放给数据分析人员，同时就引入了隐私数据泄露的风险。在限制隐私数据泄露风险在一定范围内的同时，最大化数据分析挖掘的潜力，是隐私数据脱敏技术的最终目标。目前在隐私数据脱敏领域，有一些隐私数据脱敏算法（模型）可以用来从不同角度衡量数据可能存在的隐私数据泄露风险，基础性的算法主要包括K-匿名、L多样性等。

（1）K-匿名算法。隐私数据脱敏的第一步是对所有可标识列进行移除或是脱敏，使得攻击者无法直接标识用户。但是攻击者还是有可能通过多个半标识列的特征值识别个人。攻击者可能通过社工或是其他包含个人信息的开放数据库来获得特定个人的半标识列特征值，并与大数据平台数据进行匹配，从而得到特定个人的敏感信息。如果攻击者知道某用户的邮编和年龄，就可以得到该用户的疾病敏感信息。为了避免这种情况的发生，通常需要对半标识列进行脱敏处理，如数据泛化等。数据泛化是将半标识列的数据替换为语义一致但更通用的数据。

为了解决数据发布中存在的隐私保护问题，最早由Samarati P和Sweeney L提出K-匿名（K-Anonymity）技术^[14]，并用于数据发布中保护用户的隐私。其基本思想是使同一等价类中的各个元组彼此之间无法区分，使得每条记录至少与数据表中其他k-1条记录具有完全相同的准标识符特征值，从而达到隐私保护的目的。其中K-匿名原则是要求所发布的数据表中的每一条记录不能区分于其他条记录。我们称不能相互区分的条记录为一个等价类。这里的不能区分只对非敏感特征项而言。一般值越大，对隐私的保护效果更好，但丢失的信息越多。服刑人员原始医疗数据表见表4-1所示，K-匿名后的数据表见表4-2所示。

表4-1　原始医疗数据

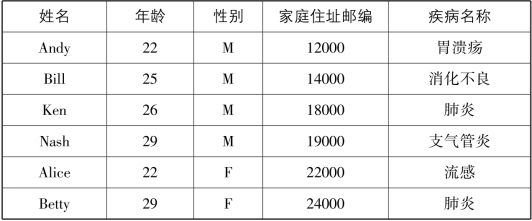
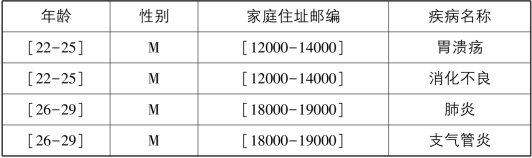
表4-2　K-匿名后的医疗数据

续表

表4-1是原始医疗数据表的部分，表4-2是对表4-1经过匿名泛化处理后得到的表，有多条记录的半标识列特征值相同（年龄、邮编），所有半标识列特征值相同的行的集合被称为等价类。显然，表4-2已将个体标识特征-姓名删除，表中等价类中的记录为2条，也即，满足2-匿名（K＝2）。作为一个衡量隐私数据泄露风险的指标，K-匿名可用于衡量个人标识泄露的风险，理论上来说，对于K-匿名数据集，对于任意记录，攻击者只有1/k的概率将该记录与具体用户关联。

（2）L-多样性算法。K-Anonymity可用于保护个人标识泄露的风险，但是无法保护特征泄露的风险，所以K-匿名后的数据仍然可能遭受攻击，例如同质特征攻击与背景知识攻击两种方式攻击用户的特征信息。为了弥补K-匿名模型的这一不足，M.A等人提出L多样性模型^[15]，该模型要求每个等价类中敏感特征值都是L良性表示（L Well-Represented），考虑了对敏感特征的约束。L-多样性定义为：如果对于任意等价类内所有记录对应的敏感数据的集合包含L个“合适”值，则称该等价类满足L-多样性。如果数据集中所有等价类都满足L-多样性，则称该数据集满足L-多样性。所谓L个“合适”值，通常就是L个不同值或者信息熵至少为Log L等等。

相对于K-匿名标准，符合L-多样性标准的数据集显著降低了特征数据泄露的风险。对于满足L-多样性的数据集，理论上，攻击者最多只有1/L的概率能够特征泄露攻击，将特定用户与其敏感信息关联起来。一般来说是通过插入干扰数据构造符合L-多样性标准的数据集，但是同数据泛化一样，插入干扰数据也会导致表级别的信息丢失。同时L-多样性标准也有不足之处。L-多样性标准无法防御特定类型的特征数据泄露，例如：倾斜攻击，如果敏感特征分布存在倾斜，L-多样性标准很有可能无法抵御特征数据泄露；相似性攻击，如果相等类的敏感特征分布满足L-多样性，但是特征值相似或是内聚，攻击者有可能从得到很重要的信息。简单来说，对于L-多样性相同的等价类，敏感特征值的分布信息对于保护特征泄露至关重要。L-多样性只是用来衡量等价类的不同特征值数量，并没有衡量不同特征值的分布，所以其在衡量特征泄露风险上仍有不足之处。(www.xing528.com)

L-多样性标准有可能很难或是没有必要实现。例如，对于服刑人员的再犯罪预测数据，预测结果列可能为犯罪或是不犯罪。对于10000条记录，可能99%的记录都是不犯罪，只有1%是犯罪。为了生成2-多样性的预测数据集，会丢失大量的信息，降低数据分析挖掘的价值。

2.隐私数据脱敏算法评价

在针对特定数据集进行隐私数据脱敏的时候，对算法做出恰当的评价是非常重要的。总体来看，面向数据挖掘隐私保护算法可以从如下几个方面进行评价。

（1）有效性。一方面指算法能够最大限度地防止入侵者非法获取隐私信息，对隐私信息进行保护；另一方面指算法能够准确地数据进行处理，在对敏感信息进行保护的同时，又不影响非敏感数据以及非敏感知识的产生。

（2）复杂性。指算法的时间复杂度和空间复杂度，这是衡量算法计算效率的一条重要标准。特别地，在分布式环境下，通讯复杂性也是一个主要因素。算法设计所追求的重要目标是设计出复杂性尽可能低的算法。

（3）扩展性。指算法处理海量数据集时的能力，或是在数据量增加时，其处理效率的变化趋势。一个扩展性好的算法在数据量增大的同时，其效率的变化是相对缓慢的。算法的扩展性在一定程度上与其复杂性相关。

3.服刑人员隐私数据脱敏

对于服刑人员个体标识信息一般可通过删除、随机数替换、哈希码替换等方法来实现数据保护。因为某些准标识特征组的取值是唯一的，为了防止攻击者通过链接攻击的方法获得个体隐私信息，对于服刑人员准标识特征可通过数据概化方法和有损连接来处理^[16].最早被广泛认同的隐私保护机制为K-匿名^[17]，它要求发布表中的每个元组都至少与其他（K-1）个元组在准标识特征上完全相同，使得其不再与任何人一一对应，然而k-匿名存在严重一致性攻击漏洞；微软研究院的德沃柯（Dwork）等人于2006年提出了差分隐私模型及差分隐私的通用随机算法^[18]：拉普拉斯机制，但该机制主要针对实数值的场合；为此，麦克雪莉（McSherry）和图沃（Tulwar）提出适用于离散值域的指数机制，也是差分隐私的经典通用算法^[19]。差分隐私假定攻击者及时知晓了原数据中的除了某一条记录之外的所有信息，仍然能提供保护，但如此高强度的保护必然带来大量的噪声，影响数据的可用性。所以在实际应用中，也出现了一些改进差分隐私的尝试^[20]。在利用服刑人员的静态特征和动态行为数据进行危险性识别与预测时，可根据数据的类型、安全级别、数据的精确度和隐私度的值来进行不同泛化的算法选择。数据隐私保护力度可通过平均泄漏概率比（Average Probability Rate，简称APR）来衡量，数据精确度（泛化后数据的可用程度）可通过加权特征熵（Weighted Attributes Entropy，简称WAE）来衡量^[21]。

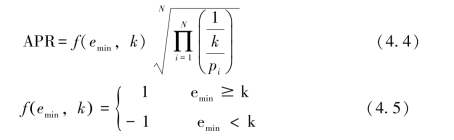
其中，N表示数据集T*中的元组数，pi＝1/ei（ei为第i个分组中的元组数）表示第i条元组对应个体信息的被泄漏率，k为数据泛化处理中每个分组中的元组数，emin表示等价组中的最小元组数.

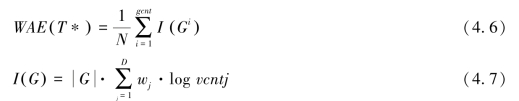
其中，WAE（T*）定义为所有元组加权信息量的平均值，I（Gi）为等价组G个特征的加权信息总量，gcnt为T*包含的等价组总数；｜G｜表示等价组G的元组数，D表示特征Aj的最大数，wj是各个特征分配的不同权重，有，vcntj是特征Aj（1≤j≤D）在等价组G上的值Vj所代表的精确值个数。实验结果^[22]发现数据的隐私度和精确度在总体上呈现相反的变化趋势，但在整个区间并不都是单调递减关系，段与段之间是逐渐增长或消减的，因此在选择较优的泛化隐私保护模型及算法时，我们可根据实际需要选择那些隐私度和精确度都优的点，也可选择那些隐私度或精确度单个优的点。