解决数据集成问题-基于大数据挖掘的服刑人员再犯罪预测

1.模式集成

模式集成主要是指如何对来自多个数据源的现实世界的客观实体进行正确识别，也即实体识别。常见的问题主要有：同名异义、异名同义等问题。例如：数据源A中的特征ID和数据源B中特征ID分别描述的是服刑人员编号和生产工具编号；数据源A中的特征prisoner birthday和数据源B中特征prisoner data都是描述服刑人员出生日期的。

2.数据冗余

数据集成经常会导致数据冗余，主要有：

同一特征多次出现；

同一特征多次出现；

同一特征命名不一致导致重复。

另外，如果一个特征能从其他特征中推导出来，那么这个特征也属于冗余特征。为此，可通过判断多个特征之间的相关度来进行判断。

（1）数值型特征的相关度。数值型特征A和B之间的相关度可以通过他们自己的相关系数rA，B来计算。公式如下：

同一特征命名不一致导致重复。

另外，如果一个特征能从其他特征中推导出来，那么这个特征也属于冗余特征。为此，可通过判断多个特征之间的相关度来进行判断。

（1）数值型特征的相关度。数值型特征A和B之间的相关度可以通过他们自己的相关系数rA，B来计算。公式如下：

其中，N为特征A和B的元组个数，ai和bi分别是特征A和B中元组i的值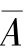，和的分别是特征A和B的平均值。

①如果rA，B＞0，则特征A和B之间是正相关，即A随着B的增大而增大，减小而减小，rA，B越大，则特征A和B越相关；

②如果rA，B＝0，则特征A和B不相关，即相互独立，这两个特征没有关系；

③如果rA，B＜0，则特征A和B之间是负相关，即A随着B的增大而减小，减小而增大，rA，B的绝对值越大，则特征A和B越负相关。

另外，需要注意的是：相关关系并不意味着因果关系，即：A和B相关，并不意味着A导致B或B导致A。

（2）非数值型特征的相关度。对于非数值型（离散或分类）特征，两个特征之间的关联度可以通过x2检验来判断。假设特征A有m个不同的类别：a1，a2，…，am；特征B有n个不同的类别：b1，b2，…，bn。则将特征A和B的不同类别值组合成一个二维表，其中特征A的m个不同的类别值构成列，特征B的n个不同的类别值构成行。假设（ai，bj）表示特征A和B的分别取值事件，即：（A＝ai，B＝bj），每个可能的（ai，bj）联合事件都在二维表中有自己的单元。卡方检验的步骤为：

①计算公式

其中，N为特征A和B的元组个数，ai和bi分别是特征A和B中元组i的值，和的分别是特征A和B的平均值。

①如果rA，B＞0，则特征A和B之间是正相关，即A随着B的增大而增大，减小而减小，rA，B越大，则特征A和B越相关；(www.xing528.com)

②如果rA，B＝0，则特征A和B不相关，即相互独立，这两个特征没有关系；

③如果rA，B＜0，则特征A和B之间是负相关，即A随着B的增大而减小，减小而增大，rA，B的绝对值越大，则特征A和B越负相关。

另外，需要注意的是：相关关系并不意味着因果关系，即：A和B相关，并不意味着A导致B或B导致A。

（2）非数值型特征的相关度。对于非数值型（离散或分类）特征，两个特征之间的关联度可以通过x2检验来判断。假设特征A有m个不同的类别：a1，a2，…，am；特征B有n个不同的类别：b1，b2，…，bn。则将特征A和B的不同类别值组合成一个二维表，其中特征A的m个不同的类别值构成列，特征B的n个不同的类别值构成行。假设（ai，bj）表示特征A和B的分别取值事件，即：（A＝ai，B＝bj），每个可能的（ai，bj）联合事件都在二维表中有自己的单元。卡方检验的步骤为：

①计算公式

其中，Oij是联合事件的观测频度（实际计数），而eij是的期望频度，可用如下公式计算。

其中，Oij是联合事件的观测频度（实际计数），而eij是的期望频度，可用如下公式计算。

其中，c（A＝ai），c（B＝bj）表示特征A和B分别取值为ai和bj时具有的元组个数。

②计算自由度df＝（m-1）（n-1）。

③依据研究者设定的置信水准，查出自由度为df的卡方分配临界值，比较它与第1步骤得出的x2统计值，推论能否拒绝虚无假设。如果步骤1计算出来的统计值大于表的值，则可以拒绝两个独立的假设，也就是说特征A和B是相关的，越相关x2值越大。

3.数据值冲突的检测和处理

数据集成还涉及数据值冲突的检测与处理。对于现实世界的同一实体，来自不同数据源的特征值可能不同。这可能是因为表示、尺度或编码不同。例如，重量特征可能在一个系统中以公制单位存放，而在另一个系统中以英制单位存放。对于连锁旅馆，不同城市的房价不仅可能涉及不同的货币，而且可能涉及不同的服务（如免费早餐）和税收。例如，不同学校交换信息时，每个学校可能都有自己的课程计划和评分方案。一所大学可能采取学季制，开设3门数据库系统课程，用A＋～F评分；而另一所大学可能采用学期制，开设两门数据库课程，用1～10评分。很难在这两所大学之间制定精确的课程成绩变换规则，这使得信息交换非常困难^[8]。

特征也可能在不同的抽象层，其中特征在一个系统中记录的抽象层可能比另一个系统中“相同的”特征低。数据集成时，将一个数据库的特征与另一个匹配，要考虑数据的结构用来保证原系统中的特征函数依赖和参照约束与目标系统中的匹配。

其中，c（A＝ai），c（B＝bj）表示特征A和B分别取值为ai和bj时具有的元组个数。

②计算自由度df＝（m-1）（n-1）。

③依据研究者设定的置信水准，查出自由度为df的卡方分配临界值，比较它与第1步骤得出的x2统计值，推论能否拒绝虚无假设。如果步骤1计算出来的统计值大于表的值，则可以拒绝两个独立的假设，也就是说特征A和B是相关的，越相关x2值越大。

3.数据值冲突的检测和处理

数据集成还涉及数据值冲突的检测与处理。对于现实世界的同一实体，来自不同数据源的特征值可能不同。这可能是因为表示、尺度或编码不同。例如，重量特征可能在一个系统中以公制单位存放，而在另一个系统中以英制单位存放。对于连锁旅馆，不同城市的房价不仅可能涉及不同的货币，而且可能涉及不同的服务（如免费早餐）和税收。例如，不同学校交换信息时，每个学校可能都有自己的课程计划和评分方案。一所大学可能采取学季制，开设3门数据库系统课程，用A＋～F评分；而另一所大学可能采用学期制，开设两门数据库课程，用1～10评分。很难在这两所大学之间制定精确的课程成绩变换规则，这使得信息交换非常困难^[8]。

特征也可能在不同的抽象层，其中特征在一个系统中记录的抽象层可能比另一个系统中“相同的”特征低。数据集成时，将一个数据库的特征与另一个匹配，要考虑数据的结构用来保证原系统中的特征函数依赖和参照约束与目标系统中的匹配。