数据质量基本理论及其应用

对数据质量进行判断，需要掌握数据质量基本理论，主要包括统计学规律、语言学规律、数据连续性理论、数据鉴别技术等^[32]。

1.数据的统计学规律

数据的统计学规律主要包括第一数字定律和小概率原理。

（1）第一数字定律。第一数字定律主要由Frank Benford对人口出生率、死亡率、物理和化学尝试、素数等各种现象进行统计分析后发现：数字1～9遵循某种规律，描述的是自然数1～9的使用频率，公式为：

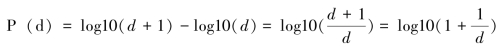
其中，d∈{1，2，3，4，5，6，7，8，9}，数字1～9的频率从高到低依次减小，具体频率见表3-7和图3-9所示。

表3-7　数字频率

第一数字定律满足成立需要满足如下条件：

数据不能经过人为修饰；

数据不能是规律排序的，比如发票编号、身份证号等。

特别提醒：第一数字定律只能发现数据质量中的“可疑现象”，但不能肯定数据质量确实有问题。在对数据进行质量分析时，需要结合领域知识、机器学习等方法综合对数据质量进行分析。

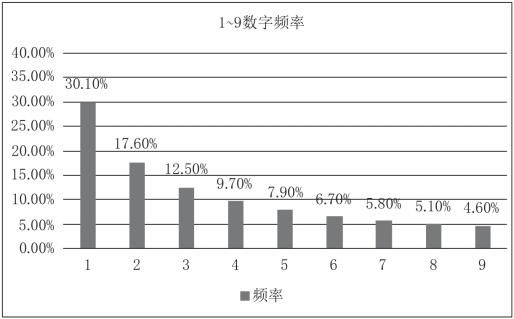
图3-9　数字频率

（2）小概率原理。一个事件如果发生的概率很小的话，那么它在一次试验中几乎是不可能发生的，但在多次重复试验中几乎是必然发生的，数学上称之为小概率原理。统计学上，把小概率事件在一次实验中看成是实际不可能发生的事件，一般认为等于或小于0.05或0.01的概率为小概率。

小概率事件在我们的生活中随处可见，它涉及生活的各个方面，掌握它很有现实意义。虽然它发生的概率很小，但它迟早会发生。虽然小概率事件有好有坏，但我们只要掌握了小概率事件的原理，在生活中就可以趋利避害，科学地选择好的小概率事件，避开不好的小概率事件。《黑天鹅》一书，核心的思想就是小概率事件不可忽视。标准差反映的是分布对期望的平均偏差，但决定我们生死的不是反映平均波动程度的标准差，而是最大不利偏差，或者说是最大回撤。

识别小概率事件的方法如下：

（1）箱线图法：处于内围之外的点即为异常点；

（2）控制图法：处于控制限之外的点即为异常点；

（3）置信区间法：处于置信区间之外的点即为异常点；

（4）预测区间法：在采用回归方程预测时，处于预测区间之外的点即为异常点；

（5）蒙特卡洛模拟：模拟结果中处于概率分布两端小概率区域的点即为异常点。

基于小概率原理，我们可以对数据质量进行分析。但是与第一数字定律类似，基于小概率原理的数据质量分析只能帮助我们识别一些“可能有问题”的数据，这些数据是否真的有问题以及存在什么问题均需要领域知识、机器学习等多种数据质量评价方法来进行综合研究。

2.语言学规律

每个自然语言都有其自身的语言学特征，这些语言特征为人们提供了数据质量分析的重要依据。频率特征分析基于如下原理：在任何一种书面语言中，不同的字母或字母组合出现的频率各不相同。而且，对于以这种语言书写的任意一段文本，都具有大致相同的特征字母分布。比如，在英语中，字母E出现的频率很高，而X则出现得较少。类似地，ST、NG、TH，以及QU等双字母组合出现的频率非常高，NZ、QJ组合则极少。英语中出现频率最高的12个字母可以简记为“ETAOIN SHRDLU”。Algoritmy网站经过科学研究，得出了字母频率统计表。此外，美国康奈尔大学数学探索项目（Math Explorer s Project）在统计40000个单词后得到了大同小异的另一表。牛津大学出版社分析简明牛津词典的词条后也得出百分比稍有不同的一表。

3.数据连续性理论

数据连续性是指由数据的可关联性、可溯源性、可理解性及其内在联系组成的一整套数据保护措施，其目的是保障数据的可用性、可信性和可控性，降低数据的失用、失信和失控的风险^[33]。可关联性是在空间维度上刻画数据连续性，是指不同数据对象之间的连续性。它是保障数据可用性的重要前提，代表了数据是否具备支持开放关联和跨域存取的能力，进而避免数据资源的碎片化。因此，研究数据可关联性的意义在于降低数据的“失用”风险。可溯源性是在时间维度上刻画数据连续性，是指同一个数据对象的历史版本之间的连续性。它是保障数据可信性的重要前提，代表了数据是否具备支持证据链管理、可信度评估以及预测分析的能力。因此，研究数据可溯源性的意义在于降低数据的“失信”风险。可理解性是在内容维度上刻画数据连续性，是指数据与其产生、管理和维护的主体（包括人与计算机）之间的连续性。它是降低数据的可控性的重要前提，代表了数据是否具备自描述和自包含信息。因此，研究数据可理解性的意义在于降低数据的“失控”风险。

在大数据时代，数据的传播、阅读和利用行为呈现了碎片化趋势，日常中，我们得到的数据往往是碎片化的数据，要进行数据挖掘，就必须进行数据的集成，为此，需要进行如下操作：

（1）将碎片化数据横向关联到其他相关数据碎片；

（2）将当前版本的碎片化数据纵向关联到历史版本的碎片化数据；

（3）将每个碎片化数据与其他相关主体（主要是指人、硬件设备、软件应用及其服务等）进行关联。

4.数据鉴别

随着信息技术的发展，数据的规模正在高速增长，然而，在数据最不断增长的同时，由于信息获取过程中的疏漏，信息传播过程中的丢失等原因，数据中普遍存在质量问题。这些数据质量问题将导致严重的计算偏差，甚至造成灾难性的后果。因此，迫切需要对数据的质量进行评估，并针对数据质量问题采取相应的措施^[34]。

数据的完整性鉴别主要包括：

数据自身的鉴别，即鉴别数据本身的完整性，判断数据是否被篡改、重放等；

数据操作主体的鉴别，即发送者的身份鉴别。

（1）数据自身的完整性鉴别。数据的完整性鉴别可使用哈希函数。哈希函数也叫Hash函数，也叫散列函数，就是把任意长度的输入数据，通过散列算法，变换成固定长度的输出，该输出就是哈希值或散列值。这种转换是一种压缩映射，也就是，散列值的空间通常远小于输入的空间，不同的输入散列成不同的输出，而不可能从散列值来确定唯一的输入值。简单地说，就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。Hash函数的值是一个固定长度的哈希值，可用H（M）表示，其中M为输入的数据，H（）为哈希函数，哈希值也叫数据的短“指纹”。目前常用的Hash函数主要有两个系列：MD和SHA系列。MD系列主要包括MD2、MD4、MD5，不幸的是这一系列的Hash函数都已经被证实是不够安全的了，我国山东大学教授王小云就是因为在有限的时间内成功地破解了MD4和MD5算法而扬名海内外。SHA系列包含SHA1和SHA2（SAH256、SHA384、SHA512）系列。其中256、384、512都是指其输出的位长度。经过长时间的测试和软硬件的不断提升，SHA1已经不再被当成是能经得住考验的选择了。目前大多数应用场景下，推荐使用SHA256以上的算法。

哈希函数具有如下性质：

抗碰撞性：对于任意两个不同的数据块，其Hash值不同，形式化为：H（M1）≠H（M2）；

抗修改性：对数据M进行任何一点修改变成M，则他们的哈希值不同，形式为：H（M）≠H（M）；(www.xing528.com)

单向性：即无法通过H（M）推导出原始数据M，形式H（M）M。

使用一个散列函数可以很直观地检测出数据在传输时发生的错误。在数据的发送方，对将要发送的数据应用散列函数，并将计算的结果同原始数据一同发送。在数据的接收方，同样的散列函数被再一次应用到接收到的数据上。如果两次散列函数计算出来的结果不一致，那么就说明数据在传输的过程中某些地方有错误了。哈希函数对数据进行完整性鉴别步骤如下：

①发送方A对原始数据使用哈希算法计算哈希值，即H（M）；

②发送方A将原始数据和哈希值组合后发送给接收方，即M＋H（M）；

③接收方B使用和发送方相同的哈希算法对收到的数据M，计算哈希值，即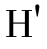（M）；

④接收方B将收到的H（M）和自己计算的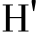（M）进行比较，如果这两个哈希值相同，则数据是完整的，否则，数据的完整性被破坏。

上述步骤是通用步骤，但是实际上是不安全的，也即不可行。如果某个恶意第三方截获这个报文，便可伪造报文，也计算一个哈希值，并将原始数据及其哈希值发送给接收方，接收方收到伪造的数据后，按照上述步骤③和④进行验证，将不能发现这个数据是伪造的，会误认为是发送方A发送的。为此，发送方需要对哈希值进行加密，我们称之为安全的数据完整性鉴别，步骤如下：

①发送方A对原始数据使用哈希算法计算哈希值，即：M-＞H（M）；

②发送方A用密钥K对原始数据的哈希值进行加密，生成报文鉴别码MAC（Message Authentication Code），即：MAC＝EK（H（M））；

③发送方A将原始数据M和报文鉴别码MAC组合后发给接收方B，即：M＋EK（H（M））；

④接收方B对收到的报文鉴别码MAC进行解密为H（M），然后再使用和发送方相同的哈希算法对收到的数据M，计算哈希值，即H（M）即：DK（EK（H（M）））＝H（M）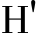

M-＞（M）；

⑤接收方B将收到的H（M）和自己计算的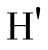（M）进行比较，如果这两个哈希值相同，则数据是完整的，否则，数据的完整性被破坏。即：H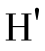（M）＝（M）？

现在有很多不同的MAC标准，最常用的是HMAC，他可以和SHA使用。

（2）数据操作主体的鉴别。数据自身的完整性鉴别主要是为保证发送方和接收方之间的数据传输数据不被恶意的第三方篡改，但并不能保证双方自身身份的相互欺骗或抵赖。例如A可以抵赖没有发生数据给B或者B伪造A发送数据。因此，需要使用数字签名实现对双方身份的相互鉴别。

数字签名（又称公钥数字签名、电子签章）是一种类似写在纸上的普通的物理签名，但是使用了公钥加密领域的技术实现，用于鉴别数字信息的方法。一套数字签名通常定义两种互补的运算，一个用于签名，另一个用于验证。数字签名，就是只有信息的发送者才能产生的别人无法伪造的一段数字串，这段数字串同时也是对信息的发送者发送信息真实性的一个有效证明。数字签名是非对称密钥加密技术与数字摘要技术的应用。数字签名必须满足以下三点功能。

接受者能够核实发送者对数据的签名，其他人无法伪造对数据的签名；

接受者确信所收到的数据和发送者发送的数据完全一样，没有被篡改；

发送者事后不能抵赖对数据的签名，这叫作不可否认性。

目前，通常采用公钥加密算法来实施数字签名，具体步骤如下：

①发送方A用自己的私钥SKA对要发送给接收方B的数据M进行数字签名（D运算），即：DSKA（M）

②发送方A把签名后的数据发送给B；

③接收方B收到A发送来的带有数字签名的数据后，用发送方A的公钥PKA进行E运算，核实数字签名，还原出原始数据M，即：EPKA（DSKA（M））＝M

上述过程满足了数字签名的三个功能。首先，如果接收方B能用A的公钥PKA核实签名，则证明这个数据是A签名的，完成报文鉴别功能；然后，如果有其他人篡改数据，伪造签名，则B用A的公钥进行E运算，就会得到不可读的数据，从而判断出这个数据被篡改，完成报文的完整性鉴别；最后，如果A要抵赖曾发送给B的数字签名，则B可把收到的数据M和数字签名DSKA（M）出示给进行公证的第三者，第三者如果能用A的公钥PKA进行E运算，得到的数据和M一样，则就可以证明这个签名就是A发送的，完成不可否认的功能。

但上述过程只完成了对数据的签名，而没有对数据进行加密，如果有恶意的第三方截获了A签名的数据，则可以用A的公钥核实签名，获得原始数据M，从而实施重放攻击。为此具有加密性的数字签名步骤如下：

①发送方A用自己的私钥SKA对要发送给接收方B的数据M进行数字签名（D运算），即：DSKA（M）

②发送方A用接收方B的公钥PKB对数字签名进行E运算加密，即：EPKB（DSKA（M））

③发送方A把加密后的数字签名发送给B；

④接收方B对收到A发送来的加密的数字签名用自己的私钥SKB进行解密后，用A的公钥PKA运行E运算，核实数字签名，即：DSKB（EPKB（DSKA（M）））＝DSKA（M），EPKA（DSKA（M））＝M。

在上述对数据M自身的完整性鉴别和对数据操作主体的身份鉴别（数字签名）中，都没有对M进行加密，则数据M有可能泄密。为此，实际工作中，需要把上述两个过程综合起来，对数据M的加密和完整性保护步骤如下：

①发送方A对原始数据M使用哈希算法计算哈希值，即：M-＞H（M）

②发送方A用自己的私钥SKA对原始数据M的哈希值进行身份认证（数字签名），生成报文鉴别码MAC，即：MAC＝DSKA（H（M））

③发送方A用生成的一次性对称密钥K对原始数据M和报文鉴别码MAC（即DSKA（H（M）））进行加密，即：EK（DSKA（H（M）＋M）

④发送方A用接收方B的公钥PKB对A生成的一次秘钥K进行加密，即：EPKB（K）

⑤发送方A将上述步骤③和④生成的数据组合发送给B，即：EK（DSKA（H（M））＋M）＋EPKB（K）

⑥接收方B收到上述步骤④发送来的数据组合后，用自己的私钥SKB对一次性密钥K进行解密，还原出密钥K，即：DSKB（EPKB（K））＝K

⑦接收方B再用还原出的秘钥K对加密的原始数据M和报文鉴别码进行解密，还原出原始数据M和报文鉴别码，即：DK（EK（DSKA（H（M）＋M））＝DSKA（H（M）＋M）

⑧接收方B用发送方A的公钥PKA对报文鉴别码MAC进行核实签名，还原出数据M的哈希值H（M），即：EPKA（DSKA（H（M）））＝H（M）

⑨接收方B对上述步骤⑦解密的原始数据M，用和发送方A相同的哈希算法计算哈希值为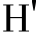（M），即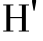：M-＞（M）

⑩接收方B将上述步骤⑧核实签名后的原始数据的哈希值H（M）和自己重新生成的哈希值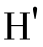（M）进行比较，如果两个哈希值相同，则原始数据M完整，否则被篡改。即：H（M）＝（M）？