电场的另一基本特性是电场力能够移动电荷做功，因此我们说电荷在电场中具有能量；如图3-1-2所示，在场强为E的匀强电场中有相距L的A、B两点，连线AB与电场线的夹角为θ，将一电量为q的正电荷从A点移到B点。若沿直线AB移动该电荷，电场力做的功W1=qELcosθ；若沿路径ACB移动该电荷，电场力做的功W2=qELcosθ；若沿曲线ADB移动该电荷，电场力做的功W3=qELcosθ；由此可知，电荷的电场中移动时，电场力做功的特点是：电场力做功与路径无关，与电荷的起始位置和终止位置有关。
图3-1-2
以上结论虽然是从匀强电场推出的，可以证明它对任意电场都成立。任何力做功都会消耗能量，电荷q从电场中一点A点移到另一点B，必然消耗电荷在电场中的某种能量，而这种能量的变化与与路径无关，只与移动电荷的电量和电场中的位置有关，所以，我们把电荷在电场中所具有的这种能量叫做电势能。
（三）电势能的大小及变化
若用EA、EB分别表示上图中电荷q在电场中A、B两点的电势能，WAB表示q从A移动到B时电场力对它做的功，则有W=qElcosθ=EA-EB。
我们知道：选择不同的零势能点，物体的重力势能不同；同样道理，选择不同的零势能点，电荷在电场中同一点的电势能有不同值，即在没有选定零势能点时EA、EB都不确定，但是，电荷q从电场中一点A移到另一点B电场力做的功不变，电势能的变化一定。即在电场中，零势能点的选择不同，同一电荷在电场电荷电势能的大小不同，但是电荷在确定的两点间移动时，电势能的变化是一定的。电场力做的功等于电势能的减少。
综上所述，只有在确定了零势能面之后，电荷在某点的电势能才有确定的值；电势能的大小与零势能面的选择有关，具有相对性；电势能的变化是绝对的，它与零势能点的选择无关。
（四）电势与电势差
1.电势
我们规定，在确定了零势能面后，单位正电荷在电场中某点的电势能是多少焦耳，那么，电场中该点的电势就是多少伏特。即电场中某点的电势定义为单位正电荷在该点的电势能，因为任何电荷在零势能面的电势能必为零，故电场中零势能面的电势必为零。
若用EA、EB分别表示电荷q在电场中A、B两点的电势能，则电场中A、B两点的电势
。
由于，正电荷在电场中沿电场线移动到零势能面时，电场力做正功电势能减小，所以电场中沿电场线方向电势必然降低，而且沿电场线方向电势降低最快。而逆电场线方向电场中的电势升高且升高最快。
建立电势概念的意义：知道了电场中某点的电势φ，就可以求出任意电荷q在该点的电势能E=qφ。
2.电势差
电势差即为电场中两点中的电势之差。
如图3-1-3，在电场中的A、B两点的电势
，所以A、B两点的电势差为
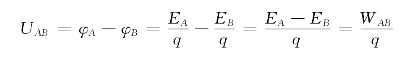
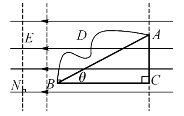
图3-1-3(www.xing528.com)
在上例的匀强电场中，
。
用d表示匀强电场中沿电场方向AB两点间的距离，则有：
Elcosθ=Ed。可以看出，电势差由电场决定，与置入电场中的电荷无关。
UAB=φA-φB=Ed是匀强电场中电场强度与电势差的关系式。
由上式可得：
，此式只适用于匀强电场。由此得到电场强的另一单位：
，可以证明：
。
在匀强电场中有：UAB=Ed。
E为匀强电场的电场强度，d为沿电场方向两点间的距离。在非匀强电场中，上式不成立。
建立电势差概念的意义：知道了电场中某两点的电势差UAB，就可以求出任意电荷q在这两点移动时电场力的功WAB，即WAB=EA-EB=qφA-qφB=qUAB。
电场力的功等于电势能的减少，等于电荷电量与电场中两点的电势差的乘积，这个结论对任何电场都成立。
3.等势面 等势面与电场线的关系
在电场中电势相等的点构成的面为等势面，在同一等势面上各点，同一电荷的电势能相等。在等势面上移动电荷，电场力不做功。
等势面必与电场线垂直。
规定在电场中相邻等势面间的电势差相等，所以匀强电场的等势面是间隔相等彼此平行的平面。
电场线从电势高的等势面指向电势低的等势面，且沿电场方向电势降落最快。在匀强电场中必有沿任意方向经过相等的距离电势差都相等。
根据等势面的特点，非匀强电场的等势面，也必垂直于电场线，且沿电场方向电势降落最快。
4.点电荷电场中某点的电势
可以证明：在选择无穷远处为零势能点时，点电荷电场中某点的电势表达式为φ=
。（按照点电荷无穷远处为零电势，可以证明地球表面的即为零势能面。）在点电荷的电场中，如果不特加说明就是以无穷远处为（或大地）零势能点的，电场中各点的电势为
。由此可知正电荷电场中各点的电势为正，负电荷各点的电势为负。点电荷组的电场中某点的电势，等于每一电荷在该点电势的代数和（电势是标量）。
5.几种典型电场的等势面
如图3-1-4所示为几种典型电场的等势面。
图3-1-4
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
