金星观测：角距离，东大距和西大距

§5-1 研究方向和对象的选定

对于月亮的研究已经基本告一段落了，现在就剩下那5颗行星了。从发现行星到现在，我们已经拖得太久了，这次我们是正经八百地开始研究行星了。

首先，我们要回顾一下，对于行星的研究我们已经有哪些初步的成果，还有之前制定的研究策略是怎样的。

不同于月亮，当我们在地球上的不同位置观测行星的时候，在1′的误差范围内，我们没有发现行星的方位有什么不同，所以虽然我们没法测到行星的距离，但是我们只需要通过研究一个地点的行星方位变化规律，就可以根据平行的规律获得地球上任何一个地点的行星方位变化规律。而要想得到一个地点的行星方位变化规律，我们只要研究行星在星图上的运动规律，再搭载星图旋转规律就可以了。由于我们在前面的研究中已经注意到行星基本上都在黄道附近，因此，我们可以初步判断行星在星图上是贴着黄道运行的。接下来，我们要具体研究一下这样的运动是什么样的。

为了区分这5颗行星，我们还要给它们命名。沿用习惯，我们分别叫这5颗行星为金星、木星、水星、火星、土星。现在又有一个问题是：这5颗行星先研究哪个呢？由于金星是5颗行星中，甚至可以说是整片天空中最亮的星，所以一方面让我们很感兴趣，另一方面也让观测较为容易。因此，我们不妨从金星开始研究。

§5-2 对金星一个周期运动的观测

虽然根据之前制订的方案，我们要描述金星在星图上的移动，但是当我们对金星观测足够长时间后，我们发现金星就像个太阳的小跟班随着太阳在星图上移动，只不过会在太阳附近摆动。所以如果我们以太阳为参照而不是以星图为参照，会让研究更加简单。由于我们已经知道了太阳在星图上的运动规律，因此，只要我们知道了金星和太阳之间的相对运动关系，就知道金星在星图上的运动规律了。

在观测的第一天，我们发现在太阳刚刚落下，天还没黑时，一颗金黄色的十分耀眼的星，我打赌是全天空最耀眼的星就显露在西方地平线上，这颗星就是金星。金星具体在哪个位置呢？我们以太阳为起点在天空中划过黄道，金星就在黄道附近。我们测量了这天金星和太阳的角距离，得到30°左右。由于天球的转动，太阳落山一段时间后，金星也跟着落山了。

在接下来的好些天里，我们发现金星都会在日落后出现，但它并不待在原地，而是缓慢地贴着黄道朝东（同样的，你从西向东朝天空划过一条弧线，这里的朝东指的是在这条弧线上的朝东）运行，也就意味着它越来越远离太阳。直到有一天，我们发现金星和太阳的角距离达到了一个最大值——46°58′。我们称此时为金星东大距，因为这时候金星运动到太阳的最东面。

东大距过后，我们发现金星不再远离太阳了，而是往接近太阳的方向移动，也因此，日落后能看到金星的时间越来越短。就这样过了2个多月，金星离太阳已经十分靠近，以至于它几乎就是跟着太阳一起落山，我们也没办法在耀眼的太阳光中辨识到它了。

看不到金星了，怎么办呢？我们猜测，金星会继续朝着一个方向运动从而到达太阳的西面，那么我们就能在日出之前看到金星。果然，一段时间后，我们发现金星在日出前从东方地平线升起了，不过遗憾的是，没过多久太阳也升起了，金星很快就被太阳的光芒淹没了。

在接下来又是两个多月的日子里，我们发现金星在日出前越来越早升起，也就意味着它和太阳的角距离越拉越大，直到有一天我们发现，金星和太阳之间的角距离达到了最大值——45°47′。我们称之为金星西大距。

从东大距到西大距，我们测量到金星所花的时间为141.8天左右，由此猜测，金星在东大距之后花了70天左右运动到和太阳最接近的方位（由于太阳的耀眼光芒，我们很难通过肉眼判定金星什么时候离太阳最近），又花了70天左右运动到西大距位置。

在金星到达西大距后，它不再往西继续移动了，而是回头往东移动靠近太阳，但是我们明显发现，这次的运动速度变慢了！果然，过了多达200多天，金星才移动到和太阳非常靠近的位置，这可比之前的70天长多了！

现在，金星又和太阳碰面，我们又看不到金星了。该怎么办呢？我们猜测，金星会继续往东移动从而到达太阳东侧，那我们就能在日落之后看到金星。果然，一段时间后，我们就在日落后的西方地平线上看到了金星。在这之后，金星继续往东移动，和太阳的角距离一天天增大，直到又过了200多天，金星到达了东大距。

我们测量到这次东大距和太阳的夹角为46°9′，略小于之前的46°58′。另外，我们测量到金星从西大距移动到东大距所花的时间为440.6天左右，也就暗示着，金星在西大距之后花了220天左右移动到和太阳最接近的方位，又花了220天左右移动到太阳的最东面。

在这之后，我们继续观测了一段时间，发现金星又回头往靠近太阳的方向运动，且运动速度和之前观察到的差不多，由此我们猜测，金星可能一直在太阳附近做着这样的往返运动，且周期为东大距到西大距再回到东大距的时间，即141.8+440.6=582.4天。我们暂且称这个周期为会合周期。

从这样的观测结果可以看出，我们只能在日落后或日出前的一小段时间内看到金星；另外，金星虽然很亮，但是当它十分靠近太阳的时候，我们也很难观测到它；还有一个比较让人不高兴的是，我们测量到的两次东大距角度和一次西大距角度，虽然很接近但并不完全相同；除此之外，还有一个更加不对称的规律是，从东大距到西大距的运行速度要明显快于从西大距到东大距的运行速度，前者只花了141.8天，而后者花了440.6天。

这些仅仅是大致的描述，还有一些比较具体的问题我们没涉及，比如金星既然不是正好在黄道上运行，那它到底是在怎样的轨迹上运行呢？还有，运行过程中的速度变化具体是什么样的呢？我们对此也进行了观测：

图5-1

如图5-1所示，横向的一条直线表示的是黄道，中间原点表示的是太阳的位置，直线下的数值表示的是标记点和太阳的角距离。图中纵向和横向的比例是相同的，而金星在这个周期的运行轨迹就是图中所画的曲线了。从这条曲线我们可以看到，金星从东大距运行到西大距的过程中是较为偏离黄道的，最远的时候和黄道的角距离达到了8°左右（虽然数值看起来不大，但是也相当于16个月亮摆在一起的距离了）；而金星从西大距运行到东大距的过程中就比较接近黄道了。另外，你还可以看到，金星的轨迹和黄道有5个交点，我已经按照金星碰到黄道的先后顺序分别将其标记为交点1到交点5（注意：图中金星从东大距出发的时候并不在黄道上，交点5是再次回到东大距时经过黄道的点），也意味着一个周期内我们会有5次机会观察到金星经过黄道。

除了轨迹外，我们还想了解金星运动速度的具体变化情况。我们在观测的时候发现了一个非常有意思的现象：金星从交点1运行到交点2花了113.2天，从交点2运行到交点3花了111.5天，从交点3运行到交点4花了113.2天，从交点4运行到交点5花了111.5天。将这些数字排列起来就是：113.2、111.5；113.2、111.5。由此我们就得到了这样一个规律：金星从黄道出发往下运行再回到黄道所花的时间是总是113.2天，从黄道出发往上运行再回到黄道所花的时间总是111.5天。

对于这个规律，我们发现以下两点可以支持它：

1）我们去测量金星从东大距出发点（很接近黄道）运行到交点1所花的时间，发现这个时间也很接近111.5天；

2）113.2天和111.5天还是很接近的，说明两个交点之间的路程越长金星的运动速度越快，路程越短金星的运动速度越慢，由此推出东大距到西大距的运行速度会远大于西大距到东大距的运行速度（注意：西大距到东大距之间有多个交点），这和我们之前的观测吻合。

§5-3 金星的偏心圆轨道模型

对于金星每天的升落规律，其实我们在观测过程中都大致了解了，结合以前的经验，我们很容易将其推广到全球，就不多说了。接下来，我们要给金星建立一个模型，即我们要猜测金星究竟在空间中是怎么运动的，才会导致在地球上观测到上述结果。建立模型的目的可以有很多，最直接的当然是受好奇心驱动，而另一方面，我们希望通过一个非常简单的模型来解释和概括所有观测结果（包括奇怪的运动轨迹），我们还希望通过这个模型预测一个周期以后金星的运动情况和一些未知的现象。

其实从金星一直跟着太阳运动出发，我们很倾向于给出这样的猜测：金星就是在绕着太阳转动。但是我们首先可以肯定的一点是：金星的轨道一定不和黄道面重合。

图5-2

如图5-2所示，如果金星轨道和黄道面在一个平面，那么我们在地球上必定会观察到金星在黄道上移动，而这和我们的观测不符。接下来，我们猜测金星轨道和黄道面成一个夹角，看能不能解释观测结果。

图5-3

如图5-3所示，金星轨道一半在黄道面上方，另一半在黄道面下方，而在交界处会对应出两个交点（图中没画出），这两个交点就是金星轨道和黄道面（注意是黄道面）的交点。金星运行到黄道面上方的时候，我们在地球上会观测到金星处于黄道的上方；金星运行到黄道面下方的时候，我们在地球上会观测到金星处于黄道的下方；金星运行到黄道面（两个交点）的时候，我们在地球上会观测到金星正好处于黄道。

根据之前的观测，金星在黄道上方运行一次的时间是111.5天，在黄道下方运行一次的时间是113.2天，由此可知金星在轨道上运行一周的时间是111.5+113.2=224.7天。但是这里有一个问题是，如果金星轨道是正圆轨道，且太阳处于圆心，那么金星在黄道面上下方的轨道长度就是一样的，而在这两段轨道上的运行时间的不同就意味着，金星在轨道上的运行是不匀速的！

我们不喜欢不匀速，因为那不好分析，而为了让金星的运动变得匀速，在保持正圆轨道（我们喜欢正圆轨道）的情况下，我们可以假设金星绕太阳的运动是偏心的，即太阳的位置偏离金星圆轨道的圆心。具体来说，我们要调整太阳的位置，使得金星在黄道面上方的轨道长度∶黄道面下方的轨道长度=111.5∶113.2。根据这个比例对一个圆进行分割，我们得到太阳偏离金星轨道圆心将近0.012个圆半径，如图5-4所示。

除了绕日周期、圆心偏离太阳程度，对于这个偏心圆模型，我们还差4个要素没确定：1） 金星绕日运行方向；2）金星轨道半径；3）金星轨道和黄道面的夹角；4）金星轨道和黄道面的交点位置。

确定了这4个要素，金星的轨道才完全确定出来。确定这些要素的方法是：我们根据这个大致模型来推测一些观测结果，而在推测的过程中，我们可能需要用到这4个要素，如果一些对这4个要素的猜测使得推测结果和观测结果吻合，我们就选择这样的猜测；如果不吻合就排除。

现在的情况是，金星绕着偏离太阳的圆心以224.7天一周的速度做匀速圆周运动的同时，太阳又绕着偏离地球的圆心以365.25636天（恒星年）一周的速度做着匀速圆周运动，那么这样的运动能不能给出我们在地球上观测到的金星运动规律呢？我们一方面要在推测过程中检验这个模型是否管用，另一方面也希望在这推测过程中需要用到这四个要素，从而确定这些要素。

金星绕太阳转，太阳又绕地球转，处理起来太麻烦了。我们可以考虑图5-5所示的方案，让问题变得简单：

图5-4

图5-5

首先，我们将参考系从原来的地球放到太阳，这样金星和地球就同时绕着太阳转了。这时候，我们使用在§3-6-2中用过的方法，让地球和金星同时减速直到地球静止，这样，地球和太阳就都静止了，只有金星在绕着太阳运动，问题就变得非常简单了。而接下来我们要解决的问题就是：经过这一番处理后，金星的绕日周期是多少呢？

金星在224.70天内转动360°，就意味着它一天转动1.6021°；地球在365.25636天内转动360°，就意味着它一天转动0.9856°。假如金星绕太阳的转动方向和地球相同（注意：这是对第一个要素的猜测），那么要让地球减速直至静止（即地球一天少转动0.9856°），金星一天就要少转动0.9856°，即它一天只转动1.6021°-0.9856°=0.6165°。金星一天转动0.6165°，那么它要转动360°要多少天呢？360°/0.6165°=583.94天，此即金星新的绕日周期。

等等，这个值非常接近我们之前测量到的会合周期582.4天！想想肯定是这样的啊，我们在地球上观测金星的时候，地球相对于我们是静止的，而我们观测的又是金星相对太阳的运动，那么太阳也就是静止了，只剩下金星的运动了，那么只有金星运动的模型自然要给出接近582.4天的结果了！

现在，如果我们让金星绕太阳的转动方向和地球相反，那么地球减速的过程中金星就要被加速，那最终得到的周期肯定会小于224.70天，从而偏离582.4天。由此，我们就可以确定，金星绕太阳转动的方向和地球一样也是自西向东了，这样就确定了第一个要素。

但是这里还有一个不大让人满意的是：582.4和583.94这两个天数不是正好相同，而是差了1天多。我们可以这样解释：因为地球和金星都不是正好绕着太阳转，而是绕着偏离太阳的不同圆心转动，而且两个轨道不在同一个平面上，所以同时减速的方案并不严格成立，这两个天数之间有差别就很正常了。不过重点是，从这两个天数很接近可以看出，我们的模型和观测结果并不存在矛盾。另外，由此我们还可以判定，这个会合周期并不是保持582.4天不变，它应该会在583.94天附近变动（为什么？）。

前面只是根据金星的圆轨道给出了一个会合周期的天数，我们还要解释一些其他现象。在不考虑地球、金星轨道的偏心和夹角的情况下，给出的会合周期和观测结果很接近，这就说明除了两个轨道偏心程度很小外，两轨道的夹角还很小。我们接下来还是忽略这两点画出平面图来分析。

图5-6是我们假想的从北黄极往下看的场景。太阳和地球仍然都不动，而金星在图中绕太阳自西向东匀速转动，绕行一周的时间在582天左右。我们接下来看这个模型能否很好地解释之前的观测结果。

1. 为什么金星在大距时的夹角基本相同呢？我们可以在图中找到东大距和西大距时金星所应该对应的轨道上的点，在地球上看，两个大距点和太阳的夹角是相等的，这和我们的观测结果很接近。你会说：“但我们测量到几个大距角度终归不是完全相等的啊！”对此的解释和之前是类似的：太阳的位置是稍微偏离金星轨道圆心的，所以如果你想象此时太阳的位置偏右一点点，东大距的角度就会比西大距的角度大点；偏左一点点，东大距角度就会比西大距的角度小点。又由于太阳偏离地球轨道圆心，因此，地球和太阳的距离会发生变化，那么这个角度也会因此发生变化。所以说角度的变化实际上和两个圆轨道的偏心都有关系，而且更深入思考后我们会发现，这个角度和两个轨道夹角还有关系。不过由于太阳偏离地球和金星轨道圆心的程度都不大，而且我们判定两个轨道夹角也不会太大，因此，我们其实也可以预测，以后我们测量到的大距角度都是在之前测量到的46°附近徘徊，不会太大也不会太小。

2. 为什么金星从东大距运行到西大距的时间要明显少于从西大距运行到东大距的时间呢？我们可以这样解释：从图中可以看出，这两段时间对应的路程是不一样的，而金星的运动是匀速的，所以自然花的时间不一样。我们还可以定量估计这两段路程的长度比例：东西大距夹角都很接近45°，那由图可以看出西大距到东大距的路程是东大距到西大距的路程的3倍左右，而之前测量到的所花时间比为440.6/141.8≈3.1倍，又是十分接近！

3. 为什么金星从东大距运行到西大距的过程中离黄道特别远，而从西大距运行到东大距的过程中离黄道特别近呢？（如图5-1所示）

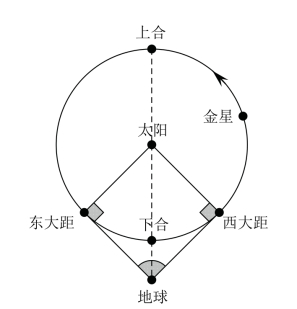
图5-6

图5-1　（副本）

你只要做这样一个想象就知道了：假如有两个小球被分开一定的距离摆在桌子上，如果你靠近了看这两个小球，你会发现它们在你视野中的张角是很大的，而如果你离远了看这两个小球，你会发现它们在视野中的张角就变得很小了。两个小球之间的距离是并没有发生变化的，只是你观测的远近不同导致它们的张角不同。同样的，金星和黄道的位置本身就有偏离，而如果我们离近了看，这个偏离程度肯定大；如果我们离远了看，这个偏离程度肯定小。金星从东大距运行到西大距的过程中和地球之间距离较近，从而看起来就和黄道夹角大；金星从西大距运行到东大距的过程中和地球之间距离较远，从而看起来就和黄道夹角较小了。

看样子，这样的模型的确是可以比较好地解释我们观测到的现象。并且不光如此，从这张图中，我们还可以获得测量金星轨道半径的方法。

图5-7

如图5-7所示，地球、太阳、东大距（或西大距）的位置构成了一个三角形，而这个三角形中有两个角是可以确定的，其中角1就是金星的大距角，而角2可以直接由视线和圆相切判定为是90°。两个角确定了，这个三角形的形状就确定了，从而我们可以获得金星和太阳的距离相对于地球和太阳的距离的倍数，结合已经获得的地球和太阳的距离（虽然之前测量的误差较大），我们就知道金星和太阳的距离了。

不过要注意到，前面的图形只是近似的二维图形，实际上金星轨道和地球轨道之间是有个夹角的，而且太阳并不处于金星轨道的中心，那么对角2是直角的判定肯定是近似的，也就意味着我们通过这样的计算得到的值也必定是近似的。不过关系，我们不妨先算一个近似的半径值，看以后有没有办法算得更精确。我们选大距角度为46°估计，可以根据三角形的形状得知这个倍数是0.72倍，也就是说金星轨道半径是地球轨道半径的0.72倍，结合之前测的地球轨道半径1.44亿千米，我们就可以估计金星的轨道半径为1亿千米左右。

现在，我们发现金星的偏心圆轨道模型可以近似解释已观测到的现象，并且我们已经得到了金星在这个轨道上的运动周期、运动方向及轨道半径，而对于这个轨道，还差夹角和交点位置两个要素没确定下来。

首先看夹角的问题，对此你可能会说：“这个夹角不就是我们在地球上观测到的金星经过黄道时其轨迹和黄道的夹角嘛！”

不是这样的！你可以想象，你面前的桌面是黄道面，而一支笔斜立在桌面上表示金星轨道穿过黄道面并和黄道面成一个夹角。然后，你将眼睛贴着桌面360°环视这个夹角，你会发现这个夹角是会变化的，而只有当你眼睛正好处于这支笔的侧面的时候，你看到的这个夹角才是真实的夹角。这个小实验暗示着，只有当我们从特定角度观测金星时，金星在星图上的运动轨迹和黄道的夹角才是真实的金星轨道和黄道面的夹角。那具体是什么角度呢？经过一番思考，我们发现，只有当地球处于太阳和金星的延长线上（即太阳、金星、地球处于一条直线）时，金星在星图上的轨迹和黄道的夹角才是真实的轨道夹角，如图5-8所示。

但是这里有个问题是：当金星和太阳在同一方位的时候，金星会完全被太阳光所淹没，那我们该怎么测量夹角呢？想了想，除非有一种可能——金星像月亮一样本身不发光，而是被太阳照亮的，那么当金星运动到日地之间的时候，我们应该会在太阳表面看到一个小黑点，这个小黑点的移动轨迹和黄道的夹角就是真实的金星轨道和黄道面的夹角了。

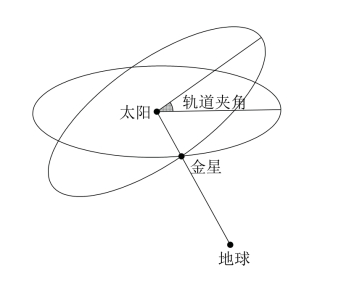
图5-8

不过，一方面我们不知道金星本身到底是亮的还是不亮的；另一方面，我们很快意识到日、金、地处于一条直线上的现象很罕见，所以这次，我们要寻求前人的帮助。如果真有金星遮住太阳的现象，人类历史这么长，应该有人看见过。非常幸运，前人的确观测到了所谓的金星凌日的现象，即他们观测到一个小黑点从太阳表面掠过，并且可以确定这个小黑点就是金星（可以通过在金星凌日现象前后一段时候观测金星的位置来确定）。据此，根据前人的数据，我们得到小黑点运动方向和黄道的夹角角度为3.4°左右，那么金星轨道和黄道面的夹角就是3.4°左右了！

解决了轨道夹角之后，下一个问题就是：金星轨道和黄道面的交点在哪里？我们也可以通过金星凌日获得。我们发现金星凌日只发生在6月8日前后和12月10日前后，这就意味着金星轨道和黄道的两个交点中，其中一个处于6月8日的地球和太阳之间的位置，另一个处于12月10日的地球和太阳之间的位置，并且6月8日对应于降交点（此时金星从上往下，或准确地说是从北往南经过黄道），12月10对应于升交点（从南往北）。不过毕竟各地有时差，而且地球进动会使得日期和星图位置错开，所以我们可以通过观测金星凌日时金星在星图上的位置来获知交点在星图上的位置，从而更准确地描述交点的位置，不过这点就不具体展开了。

两个问题都解决了，金星的轨道也就出来了！

不过，你可能还对金星凌日很感兴趣，并且会问：“多少年发生一次金星凌日呢？在降交点和升交点发生的频率相同吗？”

根据人类一直以来的记录^[1]，我们发现金星凌日的周期是这样的：升 8 ，升 121.5， 降 8 ，降 105.5， 升……循环往复。这里的升表示在升交点发生，降表示在降交点发生，中间的数字表示相隔的年份。从这个周期可以看到，一个人一生最多看到两次金星凌日，极少数人可能看到三次（年龄超过113.5岁，而且正好在出生时看到第一个降交点金星凌日）。上一次金星凌日发生在2012年6月，可见那是降交点的金星凌日，而且在2004年6月也发生了一次金星凌日，那就意味着下次就要到2117年12月了，你还有机会看到吗？

§5-4 新现象的预测

我们已经建立起金星轨道模型了，在建立的过程中，我们发现它对于已经观测现象给出了很好的解释。接下来，我们要做的事情是，应用这个模型，看能否预测一些我们未曾观测到的现象。

§ 5-4-1 金星的相

我们在测量轨道夹角的过程中有一个意外收获：金星本身不发光！在此基础上，如果我们假设金星也是一个球状物（或许在凌日时可以看到黑点呈圆形），那么回顾对于月相的研究，我们就会猜测金星也有相的变化。接下来，结合对金星运动规律的了解，我们看能否预测任何时候金星的相。

图5-6　（副本）

仍然用图5-6帮助我们分析。在东大距的时候，金星被太阳照亮一半，所以如果我们可以靠近金星或者有望远镜这样的东西可以拉近金星，我们应该会看到一个弦月状的金星。当金星从东大距往下合位置移动的时候，金星被照亮的位置越来越背向我们，所以这段时间内金星会越来越亏缺，直至完全变暗。从下合到西大距，金星渐渐变成弯月状，然后又变成弦月状。从西大距到上合，金星会越来越饱满，直至运动到上合位置变成满月状。而从下合运动回东大距，金星会从满月状渐渐变化到弦月状，完成一个相的变化周期。我们会在最后一章用望远镜来检验这个猜测。

§ 5-4-2 金星在星图上的移动

由于我们一开始就将参考系放在了太阳上，所以对于金星相对于太阳的运动，我们已经有了很多了解，而对于金星在星图上的移动，我们还一无所知。接下来，我们要通过模型来对此做一个大致的研究，不过在此之前，我们先要搞清楚地球、太阳、金星和恒星之间的相对位置关系。

在“太阳”一章中，我们说过，如果地球在绕着太阳转，那么由于地球在运动过程中看到的恒星都是静止的，因此只有两种可能：1）恒星离我们远到了太阳和地球之间的距离在它眼里只是一个点；2）恒星在跟着地球一起绕着太阳转。现在问题来了：在这两种不同假设之下，给出的金星在星图上的运动情况是不是一样的？如果是一样的，我们就没什么好说的了，预测结果只有一种；但如果不一样，我们就有两种预测结果，而在这两种预测结果中，如果其中一种符合实际观测，另一种不符合实际观测，我们就知道恒星究竟是离我们很远还是在跟着地球运动了。

我们其实希望两个假设会给出的不同的推论，但是经过一番思考后，我们发现情况并非如此……

为什么呢？我们只要转换一下参考系就知道了。我们把地球看作静止的，那么恒星就也是静止的，金星绕着太阳转，太阳绕着地球转。那么前面两种可能性的区别仅在于恒星离我们的距离，一个暗示非常遥远，一个对此并无要求，又或者说，前面两种猜测争论的是天球半径的大小（如果我们暂且使用天球模型的话）。但是不管怎样，地球都是天球的球心，那我们可以想象有两个都以地球为球心的天球：一个天球小，比如就在太阳背后一些距离；一个天球大，大到太阳和地球之间的距离都可以作为它的球心。如图5-9所示（示意图，非真实比例）。

现在，从图可以看出，无论金星在哪里，我们朝金星看过去时，它在两个天球星图上的位置都是完全重合的。那也就意味着，无论对哪个天球而言，金星在星图上的运动都是一样的！

其实，到这里我们发现，只要我们被禁锢在地球上，我们就没有任何办法区分出这两种假设的区别的！无论我们选取假设1还是假设2，对地球上的观测结果来说，都是完全等价的。那也就是说，在离开地球之前，或者找到用另外的测量方法决定恒星距离之前，我们不用太纠结到底选择这两种假设中的哪一种，我们只要选择一个好用的，可以帮助我们简单地得到可观测现象的猜测就可以了。其实很明显，我们会选择假设1，因为在这种情况下，无论地球动还是不动，恒星都可以保持静止，分析起来是更方便。

图5-9

接下来，回到原来的问题：这唯一一种金星在星图上的运动是怎样的呢？我们发现如果我们把地球视为静止的来分析会更容易。

太阳在绕着地球自西向东转动，太阳就自西向东在星图上描绘出黄道了。而金星总是待在太阳附近，那么我们可以大致判断金星会跟着太阳在星图上画出一个接近于黄道的轨迹，而且从方向上我们可以推测，金星大多数时间也是在星图上自西向东运行，但有时候可能会存在自东向西的逆行：

如图5-10所示，太阳在绕着地球转动的同时，金星绕着太阳转动。当金星运动到太阳和地球之间时，金星运动方向和太阳运动方向相反，这时候，如果金星本身绕日速度不够大，太阳就会拖着金星往同样的方向在星图上扫过；但是如果金星的绕日速度足够大，金星就可能暂时抵消太阳的束缚带来的影响，并在星图上往反方向运动，即逆行。

那金星的绕日速度是否大到能让它发生逆行呢？乍看起来这个问题很简单，太阳一天绕地球转动0.9856°（360°/365.25636），而金星一天绕太阳转动1.6021°（360°/224.70），显然金星运动得更快，那么它就会发生逆行。不过，这样的判定是很武断的，因为0.9856°对应的是在地球上看太阳在星图上一天内移动的距离，而1.6021°对应的是在太阳上看金星在星图上一天内移动的距离，一个以地球为观察点，一个以太阳为观察点，二者怎么能简单地拿来对比呢？

那该怎么办呢？即使我们不懂得计算，我们也可以通过作图得到答案：

图5-10

图5-11

如图5-11所示，我们可以先相隔1分米画出两个点：一个点表示太阳，一个点表示地球。我们再以太阳为圆心画出一个半径为0.72分米的圆代表金星轨道，并且假设此时金星正好处于地球和太阳之间（下合），这样a图就画出来了。过了20天以后，太阳会绕地球转过20×0.9856°≈19.7°，我们将图中的太阳转过19.7°，得到b图中的太阳2。当然，在这20天中金星也要绕太阳转过一个角度，不过我们在b图中暂且假设金星相对太阳不动，那么金星就会从原来的金星1运动到b图中的金星2′。最后我们再将金星2′绕太阳转过20×1.6021°≈32.0°，就得到了c图中的金星2位置。你可以看到金星2位置比金星1位置更背离太阳运动方向，这说明金星发生了逆行。

图5-12

这样，我们就解决了这个问题，我们判定金星在运动到下合位置附近时，它在星图上的运动将由自西向东的顺行变为自东向西的逆行。对于其他情况，我们再考虑一个极端情形：金星运动到上合位置时，它和太阳的运行方向是一样的，那么两个速度一叠加就会导致金星在星图上的运行速度达到最快，如图5-12所示。

现在我们就可以大致给出金星在星图上的运动规律了：金星从上合运动到下合又回到上合的这582天时间内，它在星图上的运动情况是先以高速自西向东运行，然后渐渐减低速度直至为零，然后往反方向运行，一段时间后速度又降低到零，然后又变换为原来的方向运行，直至运动到上合位置时又达到最高速度。

不过，你可能会问：“这里考虑的是一个会合周期内金星在星图上的运动，但这个会合周期是金星在星图上绕行一圈的周期吗？具体来说，金星从狮子座（或十二星座中的其他星座）出发到下次再经过狮子座所需要的时间是582天左右吗？”

肯定不是啊！由于金星跟在太阳附近，而太阳在星图上移动一周的时间是365.256 36天，那么我们可以推测金星在星图上移动一周的时间也在365.256 36天附近，所以这个周期肯定和会合周期不同！那你可能又会问：“这个周期具体是多少呢？比365.256 36大还是小呢？”从对称性来看，这个周期既不能大于又不能小于365.256 36天，但是又不大可能等于365.256 36天。那么只有一种可能是，这个周期有时候大于有时候小于365.256 36天，而其平均情况是等于365.256 36天。我们接下来就具体研究一下，看我们猜得对不对。

图5-13

如图5-13所示，假如以第一年金星下合的时候为计时起点，那么经过365.256 36天太阳绕行一周后，金星应相对下合位置转过360°/582×365.256 36≈226°，到达图示第二年的位置。我们描出这两年金星在星图上的位置，发现第二年金星在星图上的位置比第一年金星在星图上的位置偏东，因为金星此时的位置不在逆行区，所以它一定是在一段时间前就经过了第一年的星图位置（注意：顺行为自西向东），因此我们可以判定从第一年到第二年，金星在星图上的运行周期小于365.256 36天。

用同样的方法，我们可以绘制出第三年金星在星图上的位置，如图5-14所示。

图5-14

可以看到，不同于第二年和第一年的位置关系，第三年金星在星图上的位置相比第二年偏西，而金星这次同样不在逆行区，也就意味着金星还需要一段时间才能运行到第二年的位置，所以这一年金星在星图上的运动周期会长于一年。

我们还可以绘制很多年金星在星图的位置，结果都印证了我们之前的猜测：金星在星图上的运行周期会在365.256 36天附近摇摆。

不过，你可能会说：“我们还没验证在长期过程中，这个周期的平均值会不会等于365.256 36天啊！”这个简单，我们取个100年时间来考虑。100年内，金星跟着太阳一起在星图上必定也转过100圈左右，那么这100年除以约100圈，得到的平均值必定是接近1年时间的。而且不光如此，我们还可以选1000年、10 000年，选的时间越长，得到的结果肯定越接近1年。

当然，上面对于金星在星图上的运动都还只是模型给出的猜测，不过通过实际观测，我们发现它们和观测结果都吻合。

§ 5-4-3 定量研究

前面都还只是定性研究，实际上，这些定性研究在之前猜测金星轨道是偏心圆的时候就可以进行了，都不需要我们解决角度、半径（虽然考虑逆行时用到半径比）、交点等问题。而这些具体数值确定下来的具体轨道是要投入到非常定量的研究的，比如什么时候金星会运动到太阳的哪个方位，又会运行到星图上的哪个点，具体多少度多少分，等等。在原则上，我们已经完全可以根据模型来预测了，只是这个过程较为麻烦而已。

其实在进行理论推断和实际观测数据对比之前，我们在脑中就有一个对结果的期待了，我们相信对比的结果是两者很接近，但是并不会达到非常高甚至是1′的精度。为什么呢？我们在测量金星半径的时候只是近似地测量，并没有很准确，这肯定会导致最终预测结果的偏差。而实际对比的结果的确如我们所预料，模型的推测和实际结果很接近，但并没有达到非常满意的吻合度。

那该怎么办呢？如果问题只出在金星轨道半径上，我们就有可能解决。首先，我们并不需要知道实际的金星轨道半径数值或者地球轨道半径数值，只要知道它们之间的比例关系就可以进行预测。如此一来，我们可以在0.72这个比例值附近进行调整，看最后哪个比例值给出的结果是最接近观测结果的。但是非常不幸的是，不管我们怎么调整比例值，最后给出的推测结果要么是这里偏得很，要么是那里偏得很，总之，无法让所有的推测和观测结果完全吻合。那我们可能还会想到另外一个问题：会不会我们对于地球、金星轨道的偏心程度估计得不够精确呢？然而，同样的，不管我们怎么调整偏心程度，我们都无法获得完全满意的结果。

现在我们面临的处境是：要么接受这样的近似模型，要么继续寻找一个更加准确的模型。我们先来考虑一下后者，如果行就做，不行就暂时接受这样的近似模型，看以后能不能获得更加精确的模型。

§5-5 地球轨道的绘制

§ 5-5-1 策略

构成金星轨道和地球轨道（或太阳轨道）的要素有非常多，包括圆轨道、匀速性、轨道夹角、轨道半径、交点位置，等等。既然这个模型给出的精度不够，那么意味着两种可能：1）一些定性假设是错误的，比如地球轨道和金星轨道可能并不是圆轨道，或者其运动并非是匀速的；2）一些定量结果的测量误差大，比如轨道夹角、轨道半径、交点位置等。

我们应该先考虑第二种可能，把所有的定量因素都测得准确点。但是遗憾的是，当我们真地这么进行后，我们仍然得不到满意的结果。这时候，我们就想，可能是定性假设出了问题。有一个非常复杂但是有可能成功的方法是：我们不断假设地球和金星轨道中各个要素的定性或定量情况，然后看哪一种假设给出的推论最接近真实观测结果。但是这个方法所要求的工作量实在太大了！而另外一个想法是：有没有办法通过主动收集观测数据，把地球和金星的轨道一点点描绘出来呢？而且能不能同时通过计时获知它们在轨道上的运动随时间的关系呢？如果可以，它们在空间中的运动就完全确定了啊！

经过非常长期的思考和尝试，我们很幸运地发现，只要下面这两个假设成立，我们就可以首先绘制出地球轨道：1）金星每过224.7天会回到同一个位置；2）恒星远到日地间距离仅仅是一个点。

依据两个假设，我们想出了一个非常巧妙的方法绘制地球轨道：图5-15是我们从北黄极往下看日、地、金3个天体的图像，假如此时金星正好运动到黄道面（轨道交点），那这时候它们三者就都在黄道面上了。此时，在地球上是可以测量到太阳和金星之间的夹角角1的，但是为了定下这个三角形的形状（为什么要定这个形状呢？你很快就会知道），我们还需要一个角。这个角怎么获得呢？我们将目标锁定在从金星上看太阳和地球的夹角角2，而当然，我们到不了金星，没办法测量这个角，但是如果我们知道此时从太阳上看金星在星图上的位置，我们只要在地球上也看着这个位置，并且量出这个位置和金星的夹角，那么由于图中的两条虚线是平行的（根据恒星足够远的假设可推出，从地球和太阳上看同一颗恒星的方位平行），这个角就和角2相等了。

图5-15

那现在的问题就是：我们如何知道此时从太阳上看金星在星图上的位置呢？其实我们在金星凌日的时候已经观察过了啊！我们说金星凌日的时候，太阳、金星、地球在一条直线上，那么从地球上看金星在星图上的位置，就是从太阳上看金星在星图上的位置的对面，那我们只要记住凌日时金星在星图上的位置并将其转过180°，那么下次金星再次运动到同一个轨道交点（凌日点）时，我们就获得从太阳上看金星在星图上的位置了！

现在三角形的形状定了，我们可以拿出一张大纸，画一条1米长（或其他距离）的线段作为太阳和金星之间的距离，线段的两个端点就代表着太阳和金星的位置。接下来，我们再根据角1和角2画出三角形，三角形的另一个顶点就代表着地球的位置了。

不过，这还仅仅是确定了地球的一个位置，接下来，我们要确定更多的位置。

图5-16

如图5-16所示，我们只要等上224.7天，金星就又运动到同样的位置了，但是地球从位置1运动到位置2了，而我们仍然可以通过完全一样的方法来获得角1、角2，从而以这条1米长的基线绘制出新的三角形确定出位置2（如果你嫌位置2和位置1离得太远，你可以不必等224.7天，只需等113.2天或者111.5天，在金星运动到另一个交点的时候绘制地球位置）。总之，我们可以一直这样做，从而绘制出许许多多地球在空间中的点，从而渐渐绘制出地球的轨道来。虽然这里得到的只是比例图而没有真实值，不过一方面我们在预测的时候只需要比例关系；另一方面，我们之前也测量到日地距离为1.44亿千米左右，虽然误差达13%，不过可以帮助我们大致了解实际的轨道大小。

由于金星轨道半径大致是地球轨道半径的0.72倍，因此，我们拉的基线完全足够长，所以我们的精确度会相当高，这是这次测量的核心所在。

§ 5-5-2 相对性问题

这样的测量方法好像非常巧妙，不过，我们总忍不住进行一番质疑。这个方法的实施建立在两个假设上，即我们之前说过的：1）金星每过224.7天会回到同一个位置；2）恒星远到日地间距离仅仅是一个点。

第一个假设要求不高，不需要金星轨道是圆的或任何特定形状，只要它回到原来的位置就好，我们还可以通过更长期的测量把周期值测得更加精确，就当它是对的好了。主要的问题是第二个假设。一直以来，我们对于恒星的远近有这两个假设：1）恒星离我们远到了日地间距离只是个点；2）恒星在跟着地球一起绕着太阳转。而我们说过，无论我们选取哪种假设，都不会造成任何实际观测的不同，那也就意味着，不管这两个假设哪个是对的，我们都可以进行之前的轨迹绘制过程，且绘制过程和结果会完全一样。但问题是：如果在第一种假设下我们得到的轨迹是地球轨道，那么在第二种假设下我们得到的轨迹是什么呢？还是地球轨道吗？我们现在就来研究一下。

假如恒星跟着地球运动，那么我们可以画出图5-17来：

图5-17

在图5-17中，为了简单起见，我们使用天球模型，且为了让问题更加突出，我把天球画得很小。假如我们在金星凌日的时候在太阳背面看到的星图位置是M，那么经过224.7天金星回到原点，而天球跟着我们一起运动到位置2时，我们朝球上的M点看的方位是否和此时太阳朝金星（交点）看的方位平行呢？肯定会啊！虽然此时太阳看到的金星背后的星图位置不是M点了，但这并不影响两个方位平行的关系啊！

那也就是说，不管恒星是不是真的和我们一起绕着太阳转，我们都可以得到平行的结果，从而都可以获得角2，也就都可以描绘出地球的轨道。这再次说明了对于恒星的两个假设其实并不会产生什么实质性的不同，我们以后可以更放心大胆地选择比较好用的假设。

另外，我们在之前的测量中还默认使用地球绕着太阳转的模型，从而绘制出地球轨道。那你可能又会问这样一个问题：如果我们使用太阳绕着地球转的模型，那么我们能不能用类似的方法绘制出太阳轨道呢？考虑到相对性不会产生本质区别，我们相信这是可以的。

不妨也来试试：

图5-18

如图5-18所示，从地球上看太阳的时候，我们可以知道太阳的方位，一旦太阳的距离定了，它在空间中的位置就定了。而距离我们可以这样确定：运用之前的方法，我们可以测量到角1和角2，三角形形状就定了。然后，我们假定太阳到金星的距离为1个单位，那么由这段长度和三角形的比例关系我们就知道地球和太阳的距离了，从而就确定出太阳此时所处的位置。这还只是一个位置，接下来，我们要绘制其他位置。

图5-19

如图5-19所示，过了224.7天后，金星运动到和原来平行的位置，太阳也运动到了另外一个位置。我们仍然可以分别确定出角1和角2来，而太阳和金星的距离仍然是一个单位，那就可以确定出太阳和地球的距离，再结合太阳方位就可以确定出位置2来。我们可以绘制出太阳所处的很多个位置，这样就可以把太阳的轨道渐渐绘制出来了。

你看，我们可以选择地球绕太阳转的模型从而绘制出地球轨道，也可以选择太阳绕地球转的模型从而绘制出太阳轨道，那现在的问题是：我们该选择哪一种绘制方法呢？其实这是无所谓的，因为只要得到其中一个轨道，我们就可以通过变换参考系直接推测出另一个轨道。不过在这两种测量方案中，绘制地球轨道时用的基线是不动的，分析起来会更简单点，所以我们不妨选择以地球绕太阳转的模型绘制地球轨道。

§ 5-5-3 地球的椭圆轨道

绘制的方法我都已经说了，我现在直接给出绘制结果：我们发现地球轨道的确相当接近一个圆，并且太阳也的确处于偏离圆心的位置。但是经过更加仔细地审查，我们发现地球轨道更加接近一个椭圆，且太阳正好处于这个椭圆的一个焦点上。

什么是椭圆呢？准备一块木板，两个钉子，一根无法伸缩的绳子，一支笔，你就可以画出一个椭圆来。

图5-20

如图5-20所示，首先你在木板上拉开一定距离钉上两个钉子，接着把绳子首尾相连打个结形成一个闭合的绳环，然后把绳环套在两个钉子上并用笔张开绳环形成如图所示的三角形，最后保持绳环张紧的状态转动笔，你就会发现你在木板上画出了一个扁平的“圆”，这样的图形就叫作椭圆。(www.xing528.com)

我们一般叫这两个钉子所处的位置为这个椭圆的两个焦点，叫两焦点的距离为焦距，叫这个绳环的长度为这个椭圆的长轴长度。焦点、焦距这两个名字倒不算太奇怪，但为什么叫绳环长度为长轴长度呢？什么是长轴呢？

如图5-21所示，你画出一个椭圆后，过椭圆的两个焦点画一条直线，可以得到一条经过椭圆的对称轴AE，我们就叫它为椭圆的长轴。假如你在绘制椭圆时，铅笔移动到了E点，那么这时候绳环的长度就是BE长度+DE长度，这其实等于BE长度+AB长度，即AE的长度，所以我说绳环长度等于长轴长度。这个长轴的一半，我们称为半长轴，就是图中的AC或CE的长度。

我们从画椭圆的过程中可以看出：1）椭圆上每个点到两个焦点间的距离之和是一个不变的值，且这个值就是长轴的长度，这就是椭圆这种图形的本质特性；2）一个椭圆的形状和大小只取决于焦距和长轴长度，只要我们确定了这两个要素，不管我们怎么画，得到的图形都是一模一样的。如果我们不考虑椭圆的大小而只考虑椭圆的形状，决定的要素就只有焦距和长轴的比例关系，而与它们的具体数值无关了。为什么呢？这点你可以通过图5-22看出来：图中的两个三角形形状一样，也就意味两个椭圆的焦距和长轴的比例是一样的，而它们绘制出来的椭圆形状是一模一样的，只是大小有所不同而已。

接下来，我们研究一下椭圆的形状具体和焦距长轴比例是什么关系。在画椭圆的时候，通过改变钉子间的距离可以改变焦距和长轴的比例。你会发现，绳环长度不变时，两个钉子间的距离越大，我们画出来的椭圆就越扁平；两个钉子间的距离越小，我们画出来的椭圆就越圆润，越像一个正圆。所以我们可以说：当焦距∶长轴越接近1（不能达到或超过1，否则绳子会被钉子完全被张开，从而画不出椭圆），这个椭圆就越扁平；当焦距∶长轴越接近0，这个椭圆就越接近正圆。我们以后叫这个比值为椭圆的偏心率，它可以反映出椭圆的扁平或者圆润程度。

回到地球的轨道来，我们发现地球的轨道就是一个椭圆，而且这个椭圆的偏心率实际上非常小，只有0.0167，按照真实比例画就是图5-23的样子。你会发现肉眼很难区分这个椭圆和正圆的区别。另外，太阳虽然处于这个椭圆的一个焦点上，但是这个焦点离椭圆的中心非常接近，以至于太阳究竟是不是偏离这个椭圆的“圆心”也很难通过肉眼分辨。实际上这样的椭圆轨道和之前的偏心圆轨道是很接近的。

§ 5-5-4 椭圆轨道的具体位置

图5-21

图5-22

图5-23

如果说地球轨道完全是个圆且太阳处于圆心，那么这个轨道在各个方向相对天球来说就都是对称的，也就没有什么确定摆放位置的问题了。但是因为这个轨道是个椭圆，不同方向情况不同，所以我们需要确定这个轨道相对于天球的摆放位置。其实只要我们知道了轨道上一个特定点和天球的位置关系，轨道的位置就定下来了。比如我们可以选取轨道上和太阳离得最近的那一点，即近日点的位置进行研究，如图5-24所示。

怎么确定近日点位置呢？只要在地球运动到近日点时看一下太阳在星图上的位置，近日点位置就定了。那你可能会问：“我们怎么知道地球什么时候运动到近日点呢？”其实在绘制地球轨道的时候，我们完全可以将每一个绘制点对应的太阳在星图上的位置也绘制下来，这样，地球轨道和天球的相对位置关系就定下来了，地球什么时候运动到近日点自然也知道了。

当然，我们可以给出地球运动到近日点时太阳在星图上的位置，不过如果不考虑那么准确的描述，我们可以用日期来进行更直观的描述：我们发现地球会在1月初运行到近日点，在7月初运行到远日点。可以看到，地球离太阳近的时候天气反而冷，离太阳远的时候天气反而热，这说明主要决定地球气候的不是日地距离，而是直射纬度。

§ 5-5-5 面积相等的运动规律

现在地球轨道在空间中的形状和位置都定下来了，那么接下来的问题就是：地球在这个轨道上的运动和时间的关系是怎样的呢？匀速呢还是非匀速呢？如果是非匀速，则具体是什么时候快什么时候慢呢？

我们在描出地球的轨道点的同时还记录了每个点对应的时刻，从而就可以分析地球的运动和时间的关系。不过，你可能会说每两个点之间的时间间隔都达到了224.7天，两个点之间的路程也很长，不好分析。首先，我们又不是只考虑一个周期内绘制出来的点，对于不同周期绘制出来的点，肯定是密密麻麻地分布于轨道上的，我们只要将它们的时间间隔扣去365.256 36天×周期数就可以了。另外，其实还有一个解决方案：

如图5-25所示，假如我们在某一时刻发现太阳在星图上的位置是A点，那么由于我们已经知道了地球轨道的样子，也知道了它和天球的相对位置关系，下一步我们就可以过A和太阳确定出此时地球在轨道上的位置B。这也就意味着我们可以随时确定地球在轨道上的位置，我们就可以在轨道上选取任意的时间间隔来分析了。

对于如何选取轨道上的不同点或不同间隔，我们首先会想到3个方案：1）每隔相同的时间测量一次地球在轨道上的位置；2）地球在轨道上每运行一段路程记录一次时刻；3）地球每绕太阳转过一个角度记录一次时刻。

图5-24

图5-25

无疑，在这3个方案中，第一个方案是最好操作的，我们可以先选取第一个方案来研究。图5-26（a）是我画的一个夸张化的椭圆轨道示意图，在9月的时候地球处于位置1，过了30天地球运动到了位置2，又过了30天地球运动到位置3，又过30天地球运动到位置4。而通过分析这4个位置的关系，我们发现了这样一个规律：这4个位置与太阳组成的3个“弧边三角形”的面积都是相等的，即面积1=面积2=面积3！

图5-26

你可能觉得这个规律太容易猜了！其实并不是这样的。图5-26（b）是真实比例图，在这张图中，地球就像在一个圆上进行着匀速运动，所以前面的规律需要通过非常细致的测量（实际上是计算）才可以获得的。

当然，这个规律有可能只是在几个点上成立，其他点不一定成立，不过我们可以先大胆猜测：我们猜测地球在相同的时间段内会绕太阳扫过相同的面积。然后，我们可以对更多位置进行描点检验。我们发现每次检验的结果都是符合这个规律的，这样我们就对这个规律更加信任了。

在轨道已知、运动随时间变化规律也已知的情况下，我们只要知道了地球在一小段轨道上的运动情况，在其他位置的运动情况就都可以根据面积相等规律确定出来了。或者我们也不用特地考虑一小段的情况，由于地球在轨道上各个点的运动都是紧密联系的，因此只要其运行周期确定下来，各个点的运动情况就都定下来了，而这个周期其实就是恒星年周期365.25636天。所以我们现在只要确定出一个起点，就可以完全预测以后任意时刻地球在空间中的位置了！

§5-6 金星轨道的绘制

现在，地球的运动问题我们已经了解透彻了，接下来我们要研究金星的轨道了。其实在知道了地球轨道之后，金星的轨道就变得很好研究了。

如图5-27所示，假如金星处于图示位置时，地球处于位置1，那么我们可以确定金星在方位1（可以用背景星图表示），但是我们测不了距离，所以我们不知道它在这个方位的具体位置。不过没关系，过了224.7天后，金星又会回到这个点，但地球会运动到另一个点，比如位置2，那么这时候我们就还可以确定出方位2来。方位1和方位2会交于一个点，这个点就代表金星此时的位置。运用完全一样的方法，我们可以确定出非常多个金星轨道点，这样，我们就有可能将金星的轨道一步步绘制出来。

图5-27

通过绘制，我们发现金星轨道真的太接近正圆了，比地球轨道还要接近得多，不过通过更加细致的测量和分析，我们会发现，其实金星轨道更接近一个椭圆，并且偏心率为0.0068（地球为0.0167）。同样的，太阳处于金星椭圆轨道的一个焦点上。

金星轨道的形状知道了，我们自然还想知道金星轨道的放置情况。要完全确定金星轨道的放置，我们需要这几个要素：1）金星轨道和黄道面（也就是地球轨道所在的平面）的交点位置；2）金星轨道和黄道面的夹角；3）金星轨道近日点的位置。

我们首先要明确的是，我们完全可以把金星轨道在空间中一点点绘制出来，所以上面几点要素原则上我们都可以确定，只是具体该如何操作以及怎么表达的问题而已。操作的问题我在这里省略（原理已给出，省略技术内容），我直接给出这些要素的表达：对于轨道夹角，我们可以直接表达出来，我们测量到的夹角为3.395°，和之前测量到的值很接近但更准确。对于交点位置，我们仍然可以用地球上的日期表达，比如降交点在6月8日时的地球和太阳之间，升交点在12月10日时的地球和太阳之间。如果要更精确，我们应该用背景星图来表达（对于近日点位置也是如此），但是要注意，因为金星绕着太阳转，所以我们理应给出从太阳上看这些点在背景星图上的位置，具体来说，我们可以以太阳为球心，在天球上建立类似于地球经纬度的黄道坐标系，然后用黄经黄纬这些数值来表达从太阳上看到的这些点在天球上的投影。不过，这都是次要的问题了，我不具体说明了。

现在，我们还要问的一个问题是：金星在其轨道上的运行随时间的变化是怎样的？我们猜测它也符合面积相等的规律，而经过检验，我们发现的确如此。那么再结合已知的轨道周期224.70天，只要我们确定一个起点，就可以完全预测以后任意时刻金星在轨道上的位置了！

现在地球、金星的轨道，以及它们在轨道上的运行规律都确定，只剩下一个问题了：它们的轨道大小比例是怎样的？这个问题其实在原则上已经解决了。我们在绘制两个轨道的时候是以同样的比例绘制的，那么其比例关系在绘制结果中就已经体现出来了。不过这里有个问题是：对两个大小不同的圆来说，我们可以用半径比来表达它们的大小关系；但是对两个不同形状的椭圆来说，我们该怎么表达它们的大小关系呢？其实只要用长轴比来表达就可以了：金星轨道长轴∶地球轨道长轴=0.7233。而有了偏心率对长轴和焦距的搭桥，它们的焦距相对大小也就也确定了，两个椭圆之间的大小关系就确定了。

你可能会发现这里的0.7233和之前测量到的0.72很接近，并且好奇为什么。长轴是半长轴的两倍，所以长轴比实际上就是半长轴比，而半长轴可以表达近似于圆的椭圆的平均半径，因此半长轴比是更有直观意义的。我们以后就用半长轴比来表达两个轨道的相对大小，虽然它和长轴比是一样的数值。

现在，所有的比例关系及运动情况都已经确定出来了，而真当我们用这样的结果来预测金星方位的时候，我们发现预测结果和实际观测结果相当接近！这就说明这些轨道模型是非常接近真实世界的模型！

§5-7 水星轨道的绘制

接下来，我们继续研究其他行星。在剩下4颗行星中，我们发现水星是唯一一颗和金星一样被拴在太阳附近的行星，而另外3颗行星则不受太阳的拘束。既然我们对于金星的研究如此成功，而水星的运动又比较像金星，那么我们不妨先研究水星。

水星的运动虽然像金星，但它的观测要比金星困难得多（实际上它是5颗行星中最难观测的一颗）。一方面，水星远没金星那么亮；另一方面，水星可在太阳附近活动的范围更小，以至于我们只能在大距附近那几天时间内才能看得到水星。在第一个周期中，我们先观测水星达到东大距，且和太阳的距角是19.9°；过了将近47.8天，我们观测到水星达到西大距，和太阳距角是24.2°；又过了将近72.5天，水星又达到东大距，和太阳距角是27.4°。而在短暂的大距时间段内，我们发现水星的运动不是正好沿着黄道，而是在黄道上下有所起伏。

水星的观测结果和金星非常相似，这就让我们怀疑它是不是也在绕着太阳转动，并且如果是这样的话，我们首先可以从大距角度小判定，它绕太阳转动的半径要比金星小。另外，借鉴对于金星轨道的描绘经验，其实我们已经获得了描绘水星轨道的方法。不过为了实施这个方法，我们必须知道一个条件：水星绕太阳转动的周期。只要得到了这个周期，我们就可以在相隔这个周期的两个时刻分别观测水星的方位，从而用两个方位确定出水星的位置。我们尽量多地描出点就可以猜测出水星整体的轨道了。

那这个周期怎么获得呢？首先，我们可以通过会合周期47.8+72.5=120.3天来估计。如果我们假设地球静止，那么水星绕太阳运行一周的时间就是120.3天。现在，我们让地球和水星同时绕太阳加速运动，直至地球的速度变为365.256 36天转动一周，然后再看这时候水星的绕日周期是多少。刚开始时，地球静止，即一天转动0°，而水星在120.3天内转动360°，即一天转动2.9925°。考虑到我们不知道水星的运动方向，我们分两种情况讨论。

1. 如果水星和地球的运动方向相同，那么当地球加速时，水星也要一起加速。地球要在一天内多转动0.9856°，而同时水星就也要在一天内多转动0.9856°，即一天转动2.9925°+0.9856°=3.9781°，那就意味着它转上360°需要360°/3.9781°≈90.5天。

2. 如果水星和地球的运动方向相反，那么当地球加速时，水星要减速。地球要在一天内多转动0.9856°，水星就要在一天内少转动0.9856°，即一天转动2.9925°-0.9856°=2.0069°，那就意味着它转上360°需要360°/2.0069°≈179.4天。

现在的问题是：哪一个结果是正确的呢？

还记得我们在研究金星的时候是如何获得金星绕日周期的吗？我们是通过测量金星连续3次经过黄道的用时来获得这个周期的，而水星也可以这样测量。但是对于水星的测量有个问题：由于水星离太阳太近了，我们只能在大距附近进行测量，也就很难做到连续3次观察到水星经过黄道。不过，我们总有机会在水星大距时观察到它处于黄道附近，那我们就记录下这个时刻。而通过多次记录时间，我们就有可能解决前面的问题。比如，在一次测量中，我们发现水星在东大距时到达黄道附近，而下次西大距时又到达黄道附近，且它们的时间间隔是49天左右，那么我们就可以估计它的绕日周期在49×2=98天左右了。而在前面两个周期中，明显90.5天要更加接近98天，所以我们觉得真实情况很可能是第一种。当然，你可能会说，水星在黄道上和黄道下的运行时间不一定相同，对此我们总可以通过更多的观测来判定，这个问题不大。

不过即使我们知道了哪个是正确的，我们仍然面临下一个问题——从会合周期获得的绕日周期其实只是个近似值，因为会合周期本身就是在变动的！

对于这个问题，我们其实有两种解决方案：

方案1：在长期的测量中，我们总有可能测量到水星两次正好经过黄道，假如我们测量到的时间间隔为440天，那么由于这个值将近是90.5天的5倍，因此，我们将440除以5就得到88天这个更为准确的数值了。测量的时间间隔越长越准确。

方案2：假如我们有足够的耐心，连续测量了40次会合周期，并且总计时间为4635天，那么会合周期的平均值就是4635/40=115.875天，从而可以根据这个平均值计算出水星绕日周期为87.97天。同样的，测量周期数越多越准确。

我们现在就以87.97天作为更准确的周期进行轨道的绘制。不过在此之前，我们其实对水星轨道有些印象了：首先，我们之前测量到的大距角分别为19.9°、24.2°、27.4°，可见这个大距角的变化范围很大（实际上，我们发现水星的大距角大致会在18°～28°之间变化，而金星大距角只在将近45°～48°之间变化），这就暗示着水星轨道可能并不像金星轨道那样接近圆，又或者其轨道倾角很大。另外，你可以看到，一次测量到的会合周期120.3天和平均会合周期115.875天差得挺多的，这其实也暗示了前面两点。当然，我们还必须通过实际的轨道绘制来检验这些猜测。

我们最终根据描出的一些点得到的水星轨道如下：

1. 水星轨道也是一个椭圆，并且太阳也处于这个椭圆的焦点。椭圆的偏心率是0.2056，比地球轨道偏心率0.0167和金星轨道偏心率0.0068都要大得多，这就说明水星轨道的确比较扁。

2. 水星轨道和地球轨道（黄道面）的夹角为7.005°，相比金星的3.395°也要大得多。

3. 水星的半长轴和地球半长轴比将近为0.387，也就意味着如果我们把水星和地球的轨道近似看作圆，水星的轨道半径就是地球轨道半径的0.387倍。

4. 水星轨道和黄道面的两个交点中，升交点在11月10日左右的地球和太阳之间，降交点在5月8日左右的地球和太阳之间，而更准确的交点位置以及近日点的位置，可以用背景星图来描述，就不多说了。

5. 水星的运动也符合面积相等的运动规律。

首先可以看到，第一、二两点是符合我们猜测的。另外，通过这样的轨道，我们可以对水星的定性和定量观测结果进行预测。我们发现预测结果都和实际观测现象很吻合，这样我们就对这个轨道模型很信任了。

仿佛有关水星的问题都解决了，不过我们可能还会问这样一个问题：金星本身不发光，那水星会发光吗？我们同样可以通过水星凌日现象来看。首先通过交点位置可以知道，水星凌日只可能发生在每年的11月10日或5月8日，那么即使我们不去计算具体周期，也知道大致什么时候去观测水星凌日。不过非常遗憾，没人用肉眼看见过水星凌日。这就说明，水星要么本身就会发光，要么遮住太阳的部分太小。这个问题等我们有了望远镜后就很容易解决了，我们要么观测水星凌日，要么直接看水星有没有相的变化，就可以判定水星是否会发光了。

§5-8 对火星、土星、木星轨道的猜测及绘制

现在的情况是，我们已经知道了水星、金星、地球依次在以太阳为焦点的椭圆轨道上自西向东运行，运行周期依次增大，而且都符合面积相等的运动规律。我们接下来自然会猜测剩下的3颗行星——火星、木星、土星的运动也是如此了，并且根据之前观测到的其位置不受太阳拘束，我们可以判断它们的轨道必定不会在地球轨道内部，那么它们只可能接着地球轨道往外排。

当然，我们可以用之前的方法直接把剩下3颗行星的轨道描绘出来，不过在此之前，我们可以做一点铺垫工作：我们先假设我们对于它们轨道的猜测是对的，然后在这样的猜测下推测行星在星图上以及相对太阳的运动，并进行检验。如果检验结果正如我们所预测，我们就可以大胆地描绘它们的轨道，并寄希望于获得椭圆轨道、面积相等规律以及依次增大的轨道半径和周期。如果不是，我们在描绘轨道的时候就寄希望于得到另外的结果了。之所以我们要做这么一个铺垫工作，是因为描绘行星轨道是一件非常费劲的事情，我们希望在此之前对成果有一定的轮廓，以避免在这过程中因为低级错误的产生而浪费巨大精力。

首先，我们研究行星相对于太阳的运动。如果一颗行星在地球轨道外围以更长的周期（即更小的角速度）自西向东绕太阳运行，为了让地球停下来，我们得让地球和这颗行星一起减速。但是由于地球运动速度更快，因此，在地球还没减速到静止的时候，行星已经先达到静止了。那要是再往下减速使地球静止的话，行星的运动就要往反方向运行了。由此我们得到了图5-28。

从图5-28中，我们可以看到，当地球减速到静止时，行星是以自东向西绕太阳运行，从地球上看它和太阳的距角可以在0～180°之间变化。我们称它和太阳距角为0的时候为合日，和太阳距角为180°的时候为冲日。合日的时候它和太阳同升同落，我们不好观测。但合日过后，它会往太阳偏西的方向运动，从而在日出前越来越早升起，直到冲日时升起的时间往前移了一整个晚上，即在日落时升起，日出时落下。冲日时它正好在太阳背面，和太阳角距离达到最大，但从那以后它将和太阳拉近距离，升起的时间也将越来越早，直到又一次合日时跨过一整个白天和太阳同升同落……

接下来，我们再考虑行星在星图上的移动。

首先，我们来问这样一个问题：外行星在星图上的运行是单向的，还是像内行星金星、水星一样偶尔会逆行呢？

如图5-29所示，地球和外行星都在绕着太阳转动，而地球转动的角速度更大点，那从地球上看，行星在背景星图上的移动会是怎样的呢？

其实这个模型非常像我们在操场上跑步的模型。有两个学生在操场上逆时针跑步，一个学生在内道跑，一个学生在外道跑。内道跑的学生更快地跑完一圈，那么在内道跑的学生看外道的学生在看台上的投影位置是怎样变化的呢？

图5-28

图5-29

经过思考，或做真实的跑步实验就可以知道，当内道学生经过并反超外道学生时，外道学生在看台上的位置是呈现顺时针移动的，而在其他情况下都是逆时针移动。回到行星的情形我们就知道，大多数情况下行星在星图上的运动都是自西向东的，只有在地球经过并反超行星的过程中才会出现自东向西的逆行；或者说只有在行星冲日的那段时间附近才会发生逆行，并且冲日的位置正好在逆行的中点。

除此之外，我们也要对外行星在星图上移动一周的时间进行分析。这次，我们可以用极限逼近的方法：假如外行星的轨道半径非常大，大到地球和太阳之间的距离可以看作一个点，那么我们就可以认为外行星在同时绕着地球和太阳转，那么它在星图上移动一周的周期自然就是它的绕日周期了。现在，我们让这个外行星的轨道半径稍微变小点，那么地球绕太阳的运动就会对它在星图上的运动周期有一些扰动（但仍应在绕日周期附近），并且轨道半径变得越小扰动越大。而从对称性来看，扰动的方向不可能偏向任何一方，这就意味着，外行星在星图上的运动周期会在其绕日周期上下摆动，而平均值会稳定在绕日周期。

外行星相对于太阳和星图的运动都出来了，接下来，我们只要进行观测和检验就好了。在火星、木星、土星的观测中，木星非常亮，在全天中亮度仅次于金星，所以非常好观测。而火星和土星虽然不如金星、木星亮，但是相对大多数恒星来说也算是亮的了，而且火星呈红色，很好辨识。我们对于3颗行星进行长期观测，发现观测结果和我们的预测完全一致，那么接下来，我们只要去测量一下它们的绕日运行周期，就可以进行轨道的绘制了！

我们最终得到的火星、木星、土星的轨道完全是我们所预测的椭圆形轨道，太阳处于这些轨道的焦点，且也符合面积相等的运动规律。具体来说可以用一些数据描述：

火星：半长轴为地球的1.52倍，轨道偏心率为0.093，轨道倾角为1.85°。绕日运转周期为687天，会合周期为780天左右。

木星：半长轴为地球的5.20倍，轨道偏心率为0.049，轨道倾角为1.303°。绕日运转周期为11.86年，会合周期为399天左右。

土星：半长轴为地球的9.58倍，轨道偏心率为0.056，轨道倾角为2.485°。绕日运转周期为29.46年，会合周期为378天左右。

你可以看到火星、木星、土星的半长轴都大于地球轨道半长轴，且依次增大，这也就意味着它们是在地球轨道外依次排开的。另外，它们的绕日运转周期依次增大（结合半长轴的增大就意味着它们在星图上的运动周期也依次增大），这也是符合我们猜测的。不过，它们的会合周期却依次减小，这是为什么呢？

我们可以从同时减速的方案中得到解释：外行星绕日周期越长，角速度越慢，那么当地球减速到静止时，它被反向加速的程度就越大，就会越快地绕太阳转完一圈，从而会合周期就越短。另外，我们也可以从极限的思维来更直观地理解：行星绕日周期越长，角速度越慢，在星图上的移动就越慢，就越像恒星。而我们知道，太阳在恒星星图上是一年运动一圈的，也就意味着恒星和太阳之间的相对位置关系一年变化一次，那么恒星的会合周期就是一年。由于外行星和地球运动方向相同，所以一年是外行星会合周期的最低极限值，你可以看到土星的会合周期快接近一年了，这说明它本身的运动已经相当慢了。

还有一个问题是，金星本身不发光，那这3颗行星会发光吗？其实在长期的观测过程中我们发现，和恒星不一样，这3颗行星的亮度都不是一成不变的（其实金星的亮度也不是一成不变的，而水星就比较难观测了），由此，我们做这两个假设：1）这些行星自己会发光；2）这些行星反射太阳光。然后，我们根据这两种假设推测行星的亮度理应怎么变化，再对比实际情形看哪种假设较为合理。

我们先考虑假设1。如果行星自身会发光，那么按理行星离我们近的时候看起来亮，离我们远的时候看起来暗，那么结合之前的图5-28，我们就得到了推论1：当行星处于冲日位置时，它离地球是最近的，所以按理是最亮的；当行星处于合日位置时，它离地球是最远的，所以按理是最暗的。从冲日到合日，距离逐渐增加，也就意味着行星亮度逐渐降低。

从假设1进行推测很简单，但是当我们考虑假设2的推论时就遇到困难了。首先，行星受太阳的照射有相的变化，而相代表着行星那被照亮的部分有多少朝向地球，那么相的变化应该会影响行星的亮度。但是不单单相会影响行星的亮度，行星和地球的距离、行星和太阳的距离（离太阳越近照得越亮。不过这点影响较小，因为行星轨道还是很接近圆的）都应该会影响行星的亮度。这么多因素交织在一起，分析起来就很困难了。

你可能会说：“没事，我们就看实际观测结果，假如它和推论1不同，那么假设1就是错误的，从而真相只能是假设2。”

不过遗憾的是，实际观测结果就是和推论1相同，这样，我们就没法确定哪一个假设是正确的，因为假设2也可能给出推论1啊！

其实回过头来仔细想想，即使实际情况和推论1不同，难道我们就真能排除假设1吗？回顾从假设1到推论1的过程，我们会发现一个不严谨的地方：难道在行星自身会发光的情况下，太阳的光芒就不会给行星亮度带来影响吗？我们总可以想象一个自身会发光但是发光程度低的行星，太阳光给它带来的影响应该会很显著啊！

万般无奈之下，我们想到了这样一条出路：虽然在理论上因为条件的复杂我们难以推测，但我们还可以自己做模拟实验来进行判定啊！我们在漆黑的夜晚里摆一盏大灯代表太阳，然后分别在合适的位置分别摆放一个绕着大灯转动的小灯，再在代表地球的位置观察暗物和小灯的亮度变化。我们合理改变小灯的亮度（也可将亮度调成零），看在怎样的亮度下，观测结果和实际结果最接近。

不过，很可惜，我们发现小灯在亮度从零到某一特定值的很大区间里，模拟的结果都和推论1相同，而即使二者在亮度变化情况上有定量的不同，我们也很难通过肉眼进行精确判定。到头来我们就发现，我们仍然很难区分出这两个假设带来的区别。没办法，我们现在只能把这个问题先放着，等以后有了望远镜再说。

§5-9 开普勒三定律

我们之前所得到的椭圆轨道以及面积相等规律，分别就是著名的开普勒第一定律和开普勒第二定律，它们最早都是由开普勒根据第谷的观测数据发现的。不过和我们的探索有所不同的是，开普勒最早是以火星而不是以金星为参照来绘制地球轨道的，而且开普勒绘制完地球轨道后仍然认为它是个圆，等到他用新绘制的地球轨道去绘制火星轨道并发现火星轨道是个椭圆时，才回过头来发现地球轨道也更接近椭圆（这点不难理解，我们之前给出的火星轨道偏心率是0.093，是5颗行星中最大的，也就意味着火星轨道是最扁的）。虽然我们的探索过程和开普勒的探索过程有些不同，但是本质上都是三角测量法。

除了这两个定律，开普勒还发现了另外一个规律，即开普勒第三定律：行星半长轴立方和绕日周期平方的比值是定值，即a3/T2是一个常数。你可能会问这个常数是多少。周期是确定的，但对于半长轴，我们只有比例值而没有真实值，所以这个常数会随着我们选取的纸张大小而变化。当然，你可以用之前测量到的日地距离带入计算，得到所有行星轨道的半径值，从而得到这个常数；而一般情况下，我们都是直接以日地距离为单位来计算。

我们也可以想象他是怎么获得这个规律的：他把从水星到土星的半长轴和周期全部列出来，然后分别计算每个值的平方、立方、四次方等，然后看这些数值之间有没有线性的比例关系。最后他发现半长轴的立方和绕日周期的平方是同比例增加的，即a3=KT2，K是一个常数。

这样看来，开普勒第三定律的获得不是件难事，仅仅是对于数值的找规律而已。但难点在于，大多数人在得到了第一、二定律后就会觉得一切工作结束了，很少有人会去考虑半长轴和周期的关系。而且轨道参数那么多，我们事先怎么知道将目标锁定在半长轴和周期进行研究呢？我想，开普勒在发现第三定律之前，肯定也对所有的参数进行了整体的研究，并剔除那些没有明显规律的参数，最后将研究目标锁定到绕日周期和半长轴。

另外，有的人会质疑开普勒第三定律的意义：“有了前面两个定律再加上我们测量到的轨道参数，行星的运动情况就定下来了，我们何必还要加一个开普勒第三定律呢？而即使我们发现了这个规律，有必要把它提升和前面两个定律并肩的高度吗？”

在第一定律中，决定行星轨道的最重要参数是半长轴；而在第二定律中，决定行星运动速度的最重要参数是绕日周期；而第三定律将这二者联系在一起，从而使决定行星运动规律的参数变少了。所以开普勒第三定律让行星的运动规律变得更加简洁而美丽了。

§5-10 更多的问题

我们已经在目前的观测精度和可能的观测手段下得到了一个最佳模型：水星、金星、地球、火星、木星、土星都在绕着太阳以面积相等的运动规律转动，其轨道都是椭圆并且太阳处于各个轨道的一个焦点上，轨道半径和转动周期依次增大且服从开普勒第三定律。这是一个非常和谐的体系了，我们可以叫这一整个体系为太阳系。当然，你还可以考虑以地球为中心构建模型，但是你会发现它已经不如以太阳为中心构建的模型来得简单了。

现在，地球和行星已经没有什么不同了，其实我们完全可以把地球也划分为行星了。而实际上，这点对于行星究竟是什么提供了一条解释途径——既然地球是行星的组成成员，我们自然可以猜测其他行星也是类似地球的星球。不过当然，其他星球可能和地球略有不同，我们可以根据地球的很多性质分点猜测：

1. 地球是由一个固态球体加上包裹的大气层构成的，那么其他行星是否如此呢？

2. 地球是不发光的，且金星也是不发光的，那么剩下的行星是否也都不发光呢？

3. 地球存在自转，那其他行星是否存在自转呢？

4. 地球有月亮做伴（月亮是绕着地球转的^[2]），正好在所有行星中只有地球有个伴？其他行星会不会也存在这样的“卫星”？

5. 地球上有生命的存在，那其他行星有吗？

……

这些是对于行星的猜测，我们其实还有月亮以及恒星没考虑。对于月亮，我们已经知道它存在自转，这点和地球相似。我们当然还可以对照前面这些点对月亮进行猜测，而且除此之外，我们还会想的一个问题是：既然行星绕太阳转的运动都服从开普勒三定律，那么月亮绕地球的运动是否也服从开普勒三定律呢？进一步联想，如果其他行星也有卫星，其运动又会不会服从开普勒三定律呢？再进一步，其他卫星又会不会符合前面对于行星的猜测呢？

……

最后，我们考虑恒星。以前我们说过，在地球绕着太阳转动的情况下，恒星只有两种可能：1）远到日地间距离在它面前只是个点；2）跟着地球绕着太阳转。考虑到二者对于地球上的观测毫无区别，我们之前选择了较为好用的前者。现在，地球沦为了行星，失去了特殊地位，那么恒星跟着地球运动就变成了一件非常巧合的事情（恒星为什么不跟着其他行星运动呢？），所以从可能性而非实用性角度来说，我们觉得第一种假设比较可信。而由第一种假设来看，恒星离我们是难以想象得遥远，而在这么遥远的情况下我们居然还能看到恒星，说明恒星本身必定是非常亮的。我们见过的最亮的天体是太阳，那我们就会猜测，恒星会不会是非常遥远的太阳呢？进一步想象，这些非常遥远的太阳又会不会也存在自己的行星呢？如果是这样的话，整个世界就是由一个个相隔非常远的太阳（或者我们其实可以将太阳纳入恒星的范畴）带着它们各自的行星组成的了！

当然，这些都还只是猜想，还需要等我们的观测能力得到提高后才可以检验。我们留到最后一章中解决。

§5-11 补充内容

到此为止，我们已经完成了既定目标，将恒星、太阳、月亮、行星依次研究了一番。我们可以将这些天体分为两类：一类是相对位置基本不变、组成星图的天体；还有一类是会在星图上移动的天体。现在，对应于我在第二章补充内容中引入的两种新的第一类天体——银河和星云，在这章的补充内容中，我将引入两种新的第二类天体——流星和彗星。

§ 5-11-1 流星

当我们仰望星空的时候，有时候会看到天空中有亮线十分迅速地划过天空，并且大多是朝向地面的，仿佛是一颗星星坠落了，这就是我们所说的流星。我们看到的大多数流星都是白色的，不过流星也有蓝色、红色、黄色、绿色、紫色等颜色，而当你仔细观察它们时，你甚至会发现有的流星在划过天空的过程中会变化颜色。不光是流星的颜色丰富多彩，流星的亮度也不是一成不变的，从暗得几乎看不清到亮得刺眼的都有。另外，流星的大小和划过的长度也各有不同，有的划过一小段距离就消失了，有的可以一直划过半片天空直至地平线。有一些特殊的流星，非常像一团带着长长火焰尾巴的火球，亮度非常高甚至亮得刺眼，能划过较长的距离，并且有的划过后还会产生声响或者留下尘埃余迹，我们对它们比较感兴趣，并专门给它们起了一个名字——火流星。

流星并不是像大多人想象得非常罕见，其实任何一天晚上，只要天气晴好，我们平均一小时就能看到三四颗流星，这些流星都是偶发的，它在哪个方位出现、什么时候出现、具体朝哪个方向划过等都没有明显的规律。但是随着继续观察我们会发现，有时候会出现一群不偶发的流星，这些流星仿佛是从天球上的一个点辐射出来的，而且流量明显比平时增大。这样，我们就可以区分出两类流星：一类是无规律的偶发流星；另一类是从天球上一个点辐射出来的流星，我们称之为流星雨。

偶发流星的出现没什么规律，也就没什么好研究的了，而流星雨的出现有一定的规律，所以我们重点来研究一下流星雨。我说流星雨是从天球上的一个点辐射出来的，这会给人一个错误的印象，仿佛流星雨就是一瞬间从一个点迸发出来的。其实不是这样的，流星雨往往能持续几天甚至一个月，在这段时间内，我们时不时会观察到有流星从天球上的某个点辐射出来，并且多数时候流量不大，只有在某几个小时内流量会比较高，我们称之为流星雨的极大。对于某些较大的流星雨，极大时流星数量可以达到一小时上百颗，更强劲的流星雨极大时流星数量一小时可达上千颗，对于后者，我们也称之为流星暴。

还要注意的是，我这里说的辐射点指的是天球上的一个特定点，并不是天空中的某个方位，这两者是有所区别的。说到天空中的某个方位，它是固定的，但是天球星图是在转动的，所以当我们观察一晚上后，流星雨的辐射点可能就从东方天空移动到西方天空了。我们经常听说某某座流星雨，比如双子座流星雨、狮子座流星雨等，这里的星座指的就是这个流星雨的辐射点所在的星座。这就产生一个问题了，如果一些星座包含不止一个辐射点（比如宝瓶座就有三个，猎户座有两个等），那我们该怎么区分不同的流星雨呢？这是人为区分和命名的问题，算是科学研究中最简单的问题了，我们总有很多办法来解决，比如我们可以以这个星座上离辐射点最近的恒星来区分不同的流星雨。

我们还想研究一下流星雨发生的时间规律。具体来讲，我们可以年复一年地观测所有流星雨，然后把每一次流星雨对应的辐射点位置以及发生的时间记录下来，看有没有什么规律。我们发现一年中较明显的流星雨数量可以达到几十个，每一个流星雨对应于一个独有的辐射点，并且每一个辐射点对应的流星雨都是一年发生一次，且每年发生时的公历日期都是相对固定的。如果我们观察的年份足够多，我们还会发现流星雨的流量总是会波动，有的波动范围小且好像没什么规律（或许也和观测天气的无规律波动有关），但有些就波动范围大且明显存在周期性的变化规律了，比如狮子座流星雨（发生在每年的十一月中旬）每隔33年出现一次流量非常大的流星雨，在极大时可以达到每小时上千颗（它也因此获得了“流星雨之王”的称号），但是在爆发之后流量却逐年减少，没过多久就还不如普通的流星雨了。

流星雨的流量有大有小、亮度有高有低，也就使得我们对于不同流星雨重视的程度不同。对居住着大多数人口的北半球来说，一年中有三场流星雨是流星亮度较高、每年流量较大而稳定的，我们把它们称为北半球三大流星雨——象限仪座流星雨（1月初）、英仙座流星雨（8月中旬）、双子座流星雨（12月中旬）。对于象限仪座流星雨，你可能会发现在全天88星座中找不到象限仪座，这仅仅是因为当初划分88星座的时候我们没有把象限仪座囊括其中，而这个流星雨的名字又沿用了习惯而已。象限仪座流星雨的辐射点大概在牧夫座和天龙座之间。

我们现在自然非常好奇流星到底是什么，流星雨为什么会在每年的特定日期从特定的星图位置辐射出来，有的流星雨流量又为什么会呈现周期性的变化等。我们可以来做一些猜想。

流星划过天空的速度是非常快的，这就暗示着流星是离地球比较近的。另外，我们发现流星大多往地面方向划动，这就暗示着流星可能是某种受重力作用坠向地面的东西。由此我们猜测可能真的有什么东西从天而降。实际上的确如此，人类一直以来就有陨石坠落的记载，即我们发现一部分火流星坠落后，在地面砸出一个坑，并在坑内有烧焦的陨石。不同陨石的成分有所不同，有的就像普通的石头，有的还带有金属……

不过，这里有个问题是，流星那么常见，为什么我们没有经常发现陨石坠落呢？其实无论从陨石坠落前带的明亮火焰，还是从陨石明显受到烧灼的痕迹来看，流星在空中应该是处于燃烧状态的，那么对于较大的流星体（为了区分，我们可以称坠落前为流星体，坠落后为陨石），可能被燃烧了一部分后还有一部分保留从而可以成功着陆成为陨石，但对于较小的流星体而言，可能在着陆之前就燃烧殆尽了。但这里又引出一个问题，流星体为什么会燃烧？难道它本身就是燃烧着的天体？但如果是这样的话，为什么我们只能在它坠落前几秒才看得到呢？

我们不妨发挥想象力，考虑一些其他解释：或许流星体本身是非燃烧状态的，只是当它闯入大气层后和大气层摩擦从而燃烧起来。但是这里仍然有一个问题是：流星体是石头或金属一样的东西，而这些东西是无法燃烧起来的，那流星体在坠落前怎么可能处于燃烧状态？

其实任何物体，尤其金属被烧灼到一定的程度后都是会自己发光并产生火星的，那么当流星体被摩擦到一定程度，温度升得足够高后，就可能发出光芒并产生火星，运动快了就可能看起来像在燃烧了。当然，这些只是猜测，到底对不对还需要以后的探索来检验。不过重点是，我们可以大致确定，流星的出现的确是某种离地球较近的流星体坠入大气层导致的。

接下来的问题是，我们该如何解释前面说的偶发流星和流星雨的出现规律呢？

我们可以这样猜测：可能在整个地球轨道上就存在一些没有特定运动规律、四处乱飞的流星体，有的偶然飞进大气层就形成了偶发流星。而除此之外，在地球轨道附近还有一些地点储存着很多流星体，这些流星体每时每刻都在从存储地向外辐射，当地球经过这些地点时，这些流星体就会进入地球的大气形成流星雨。

如图5-30所示，假如某个星座流星雨的流星体都来自图中所示的一个辐射点，而且这个辐射点非常接近地球轨道，那么每当地球运动至这个辐射点附近时，就会产生流星雨，且地球最靠近这个辐射点的时候，就是流星雨极大发生的时候。我们可以让这个辐射点处在一个特殊位置，使得其所处星图背景位置正好在这个流星雨对应的星座上。由于地球一年会经过辐射点一次，因此，流星雨一年发生一次。

这样的假设可以解释已知现象，但我们还要根据这个假设给出新推论。在这个假设中，由于辐射点离地球很近，因此当地球经过辐射点的时候，辐射点在星图上的位置应该会有明显变化。可是当我们去检验的时候却发现，在流星雨发生期间，辐射点在星图上的位置是基本上没有变化的！另外，仍然从辐射点距离地球较近出发我们可以推测，在地球上不同地点看到的辐射点在星图上的位置是不一样的。但实际情况是，不同地点观察到的辐射点位置是完全一样的！

除了推论有问题外，这样的假设还有点不可思议。为什么那么多流星体会从一个虚无的点爆发出来？而即使我们假设这个地点有某个天体存储了很多流星体，那为什么我们从来都没看到过这个天体？

图5-30

现在，这个假设看上去有点问题，我们不妨再考虑其他假设。首先，我们可能要抛弃流星体被存储于一个地点并辐射出来的想法了，因为一旦我们如此假设就陷入之前的困境。那现在的问题是：在不如此假设的情况下，怎样的假设才能造成流星体从一个地点辐射出来的现象呢？

我们想起了平时的生活经验：当我们朝着平行的两条铁轨向远处望去时，我们会发现两条铁轨趋于相交；或者我们在繁华都市的地面朝上看许多摩天大楼的时候，我们会感觉摩天大楼越往上越互相靠近。

这样的经验就给了我们一个灵感，假如流星是平行地朝向我们运动，那么当我们抬头看这些平行流星的时候就会有种错觉：它们仿佛是从一个点辐射出来的。而且在这样的假设下，辐射点位置的不变就可以得到解释了。具体来说，我们可以这样假设：

如图5-31所示，在地球轨道上的部分区域分布有一些密集的静止流星体，每当地球经过这些区域时，由于地球朝着一个方向运动，因此，流星体在我们看来就是往相反的方向平行运动，从而就像是从一个地点辐射出来的。

这个假设会给出一个推论——地球朝向哪个星座运动，流星雨的辐射点就在哪个星座。但是事实并非如此！因为在这种情况下，辐射点就只可能处于黄道十二星座，但是很多流星雨并非如此，比如象限仪座流星雨和英仙座流星雨。（到这里，我们突然意识到，在之前的辐射点假设中，我们忽略了流星雨星座和日期的对应关系）

我们不得不再次修改假设：如图5-32所示，我们假设流星体们也存在着彼此平行的运动，且它们的运动轨迹会经过地球轨道，那么当地球运动到这些流星体经过的轨道区域时，地球的反方向运动和流星体的运动一叠加，就会在整体上产生一个新的方向的运动。流星体运动的方向可以是任意的，那么只要适当假设，两个运动叠加后的总运动方向也就可以是任意的，从而其反方向就可以指向任意星座。（这里涉及一些运动学知识，如果看不懂没关系）

从流星雨每年都会发生来看，流星体的轨道应该是稳定的，那我们很倾向于猜测流星体轨道是一个闭合轨道，且结合太阳系中的行星都绕太阳做椭圆轨道运动，我们也会更进一步猜测流星体也是绕太阳做椭圆轨道运动的。这样会引出一个推论：由于流星体每年都会被地球吸收掉一部分，因此它的数量应该会逐年减少，也就意味着任意一场流星雨的流量都会逐年减少。但是问题是，虽然我们的确注意到有些流星雨流量逐年减少，但是它经常可以在一些年份获得补充。最典型的例子是狮子座流星雨，它每过33年流量大增，而后流量渐渐减少，又33年流量大增，而后又渐渐减小……仿佛每过33年就有什么会补充一下狮子座流星雨的流星体。除此之外，还有些流星雨流量每年都比较稳定，对此我们可以有两种解释：1）每年又或者更短期内这些流星雨的流星体都会获得补充；2）稳定流星雨对应的流星体数量是很庞大的，地球的消耗对它而言其实是微不足道的。不过就那些流量存在周期性变化的流星雨而言，就留下一个问题：是什么一直持续补充着流星体？我们先放着，看以后能不能解决这个问题。

图5-31

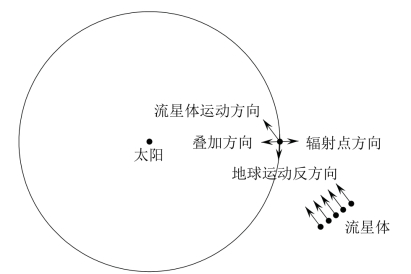
图5-32

§ 5-11-2 彗星

接下来，我们研究一下彗星。

从古至今，人类就一直观测到天空中偶尔会出现一颗带着长长尾巴的天体，其形似扫帚，因此中国古人称之为“扫帚星”。作为现代人，我们称之为彗星，并把那长长的尾巴称为彗尾，把最为明亮的头部称为彗头。

我们平均一年可以用肉眼看到一次彗星。当我们观测多了就会发现，彗星的长相并不是一成不变的，不过其主要区别只体现在彗尾上——有的彗星彗尾较长，有的彗星彗尾较短，有的彗星还有很多个分离的彗尾。彗星的颜色很多样，红色、绿色、白色、蓝色等都有。彗星可见的时间长度也有所不同，有的只在几天时间内可见，有的好几个月都可见。这些都说明彗星不大可能只是一个天体，而应该是一类天体。

彗星不像流星一样一闪而过。当我们观察彗星的时候，其实就像在地面观察普通星星一样，很难在短时间内看到它的方位变化，这其实暗示着彗星离我们是比较远的。除此之外，彗星也像太阳、月亮、五大行星一样在星图上缓慢移动，这可能意味着彗星是在太阳系内移动的。我们对很多彗星进行观察，发现它们的运动都有如下规律：1）彗星先是朝着太阳的方向运动，然后在经过太阳后又开始远离太阳运行，直到最终越来越暗淡并消失在视野中；2）彗星在运动过程中，其彗尾始终背向太阳，而且越靠近太阳彗尾拉得越长。这点让我们不禁遐想，彗星会不会是某种冰状的物质，它受到太阳的照射后变为冰粒、水滴或水蒸气从而形成彗尾。

彗星显然不可能突然出现，它或许是从太阳系以外的地方闯入太阳系，而后又匆匆离去。我们想要绘制彗星轨道，但这次不像绘制行星轨道那么简单了，因为这要求彗星连续两次经过同一个位置，而目前的情况显然无法满足要求。不过，我们仍然可以对彗星轨道做一些猜测：彗星总是朝向太阳运动而后又远离太阳，其实这非常像外行星的运动。那彗星会不会也在绕着太阳运动，且其轨道也是椭圆形，只不过这个椭圆非常扁而长，从而只有一部分处于太阳系内？而这样的假设立马给出一个推论：同样一颗彗星会周期性地被观测到！

等等！还有没有这样一种可能——彗星喷洒出的彗尾其实就是流星体的来源，而彗星的周期性拜访就像一把粉笔，不断地在轨迹上留下流星体，从而对流星体进行补充！而这样的假设立马给出了这两个推论：1）假如彗星真的是流星体的来源，那么这个彗星的轨道必定和地球轨道相交，且彗星在这个交点的运动方向就是流星体的运动方向，从而这个运动方向和地球运动反方向的叠加方向的反方向就指向辐射点（像我刚才说的，这点不理解没关系）；2）每当彗星拜访太阳系的时候，假如它是一场流星雨的来源，那么它都会引起对应流星雨的爆发。具体来说，我们可以推测，狮子座流星雨流量33年的变化周期暗示着存在一颗每33年拜访一次太阳系的彗星。

图5-33 彗星

但是真到了检验的时候，我们就遇到困难了。首先，对于1）的检验，我们没办法绘制彗星的准确轨道，也就很难检验它是否和地球轨道相交，更别说检验彗星运动方向是否和流星体相同了。而对于2）的检验，虽然我们的确发现一些彗星的到来正好和一些流星雨爆发的时间很接近，但是我们很难做到非常多次的检验，从而就很难排除偶然性。

其实可以想象，如果要严格判定彗星和流星雨的关系，我们必须得绘制彗星轨道。而且还有一个问题是，我们刚刚猜测彗星是一个冰状物并喷射出冰粒、水滴、水蒸气这类物质，但是这些东西好像很难解释陨石的现象。难道彗尾还包含有其他物质？我们将这些问题放着，留到最后一章中解决。

【注释】

[1]其实我们很难通过经验性观测获得这个周期，因为金星凌日并不是那么容易观测的现象。实际上我们是通过结合轨道计算预测和观测检验来获得这个周期的。

[2]这点你可能会质疑，因为我们之前也考虑过地球绕着月亮转的模型。可问题是，如果我们让地球绕着月亮转，那么月亮就变成绕着太阳转的行星了，可我们不知道在这种情况下月亮是否也服从开普勒三定律啊！而我们可以确定的是，如果让地球绕着太阳转，那么地球是服从开普勒三定律的，那么我们让地球作为行星的成员，所有行星不就都服从开普勒三定律了？