黄道上升落规律及关键点

§3-1 模型的选择

接下来我们研究太阳。按照前面制定的研究策略，我们应该在地球上找一个地点观察太阳在星图上的移动，然后用旋转规律给出每天太阳在天空中的方位变化，再结合平行规律推测其他地点的观测结果。不过，我们其实可以将一个地点的观测结果直接加入之前建立的模型，然后运用模型推测任何一个地点的观测结果。

首先我们要开始选择模型。在对太阳的研究中，1）我们不关心恒星的远近问题以及恒星究竟是什么的问题，所以我们可以使用最简单最好用的天球模型；2）恒星星图要花几百上千年才会有微小的变化，所以我们假定天球上的星图不变；3）地球的进动要用3年时间才可以察觉到，说长不长，说短不短，为保险起见，不妨考虑这项。最终我们选定的模型就是这样的：

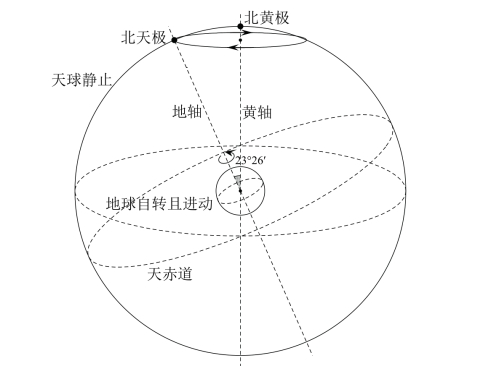
图3-1

如图3-1所示，恒星固定在天球上组成不变的星图，天球和黄轴保持固定，而地球（当然，这里的地球被我明显画大了）在绕地轴自转的同时和地轴一起绕着黄轴进动。

在图3-1中，你还注意到我把赤道放大直至在天球上截出了一个大圆，我们称这个大圆为天赤道。天赤道相对于天球星图的位置和投赤道相对于投影球星图的位置是相同的，所以实际上天球和天赤道就是投影球和投赤道的放大版本。这同时意味着，在天赤道上的恒星都是从正东方升起从正西方落下，在天赤道以北的恒星都是从东偏北升起从西偏北落下，在天赤道以南的恒星都是从东偏南升起从西偏南落下……

无论是太阳、月亮还是行星，当它们在天球星图上移动从而变为“不同恒星”时，就会遵循不同的升落规律。我们接下来就是要先研究太阳在天球星图上的移动，然后根据模型得到任何一天在地球上任何一个地点的太阳方位变化规律。

§3-2 一个周期观测的结果

我们可以在地球上任意选择一个地点进行观测，不妨选择人口较为密集的北纬40°地区进行观测。经过将近365.2天的观测，我们发现了一个非常简洁的结果——太阳在天球星图上的运动就是绕着黄轴的自西向东运动！

如图3-2所示，我把原来垂直于黄轴的虚线圆画成了实线，这实际上就是太阳在星图上的运动轨迹，我们可以叫它黄道。这个黄道还和天赤道有两个交点，分别被我标为了H1、H3，也就意味着当太阳运动到这两个点时，我们在地球上会看到太阳从正东方升起从正西方落下。我还在黄道上等分出了H2、H4两个点，它们是黄道上最为远离天赤道的位置，也就意味着当太阳运动到这两个点时，其升起和落下的方向都最为偏离东西方向。

还有一个问题是：太阳在这个黄道上的运行是不是匀速的呢？我们发现太阳从H1点移动到H2点花了将近92.7天，从H2点移动到H3点花了将近93.6天，从H3点移动到H4点花了将近89.0天，从H4点回到H1点花了将近89.9天。同样的路程，所花的时间不一样，这就说明太阳在黄道上的运行不是匀速的。不过话说回来，考虑到这些天数总体来说还是比较接近的，所以太阳的运动总体来说还是比较匀速的。

除了发现太阳在星图上的运动如此简单外，我们在观测过程中还发现了一个很有意思的现象：在整个周期的观测过程中，月亮、5颗行星都在黄道附近！

对此，你可能不觉得惊讶了，因为我们之前在发现行星的时候也发现了一个类似的规律：5颗行星近似地处于星图的一个大圆上，并且月亮和太阳也总在这个大圆的附近。而现在我们发现，黄道就可以作为这个大圆！并且我们发现，在这将近365天的观测周期内，月亮和5颗行星总是在这个黄道附近，这就说明它们很有可能总是贴着黄道运行的！所以如果我们以后想要寻找黄道，只要联结这些天体中的任意两个，在天空中扫过一个大圆就可以大致确定了。

接下来你可能会提出这样一个问题：“我们仅仅观察了太阳在一个周期内的运动，那在以后的日子里，太阳会不会一直重复着这样的运动呢？”

为了解决这个问题，我们可以在这个周期过后多观测了几天。我们发现这几天太阳又重复了之前的运动，这就说明，很有可能这样的周期运动会一直重复下去。除此之外，还有一个意外发现给太阳的周期运动提供了支持：太阳在星图上移动一周的过程中，气候也变化了一个周期——太阳从H1移动到H2，再移动到H3、H4，又回到H1的过程中，气候是渐渐从温暖变为炎热，再从炎热变为凉爽，再从凉爽变为寒冷，最终又变为温暖。而从太阳光携带热量、昼夜温差变化等出发，我们会觉得这样的因果关系很可能成立：太阳的周期性运动是气候周期性变化的主要原因。而反过来，气候的周期性变化，可能就暗示着太阳的周期性运动。因此，虽然我们只观测了一个周期内的太阳移动，但我们从出生开始就一直感受到气候的周期性变化，并且我们相信今后气候仍然会如此变化，所以我们有理由猜测，无论是以前还是今后，太阳都进行着这样的周期性运动。

图3-2

但这里就还有一个问题是，虽然气候变化的周期性能给太阳运动的周期性提供一些支持，但这是否就意味着太阳的每一圈运动都是完全相同的？比如，每转动一圈的时间是不是总是相同？或者在每个轨迹点上的运动速度是不是总是相同？

首先，从之前那一个周期后额外研究的几天的数据来看，太阳的确是完全重复之前的运动，所以我们猜测可能太阳每圈的运动都是相同的。另外，我们也可以从气候变化来看：虽然每年的气候都会略有不同，但从长期来看，气候变化还是比较稳定的，这可能就暗示着每年太阳的运动都是基本相同的。不过当然，我们也很难从这里下定论，因为一方面气候并不容易定量测量，另一方面影响气候的可能不止有太阳（你会发现地球上不同地区的气候会有所不同）。

实际上，如果转换一下思维，把重点放在研究气候而不是研究太阳上，你就会发现，我们可能通过研究太阳的运动来了解气候的变化。比如，我们可以通过测量太阳的运动周期来获得气候变化周期。

你会发现，对于气候变化周期的测量是很困难的。你不能说你从某年夏天感觉最热的时候开始计时，然后等到明年最热的时候停止计时，因为你根本无法准确判断哪天是最热的！那你可能说，既然如此，气候变化就没有周期，因为我们测量不到。但是可以想象，如果我们测量相当多年（其实一年的原始定义就是气候变化周期）气候变化的总时间，再除以年数，就可能得到一个相当稳定的值。而现在，通过测量太阳的运动周期，我们或许可以不用花那么长时间就直接获得气候变化周期——365.2天左右。当然了，我们还要估计误差：由于太阳在星图上平均一天移动59′（可由365.2天移动360°计算），那么移动1′就需要将近24分钟，而在这24分钟时间内，我们不知道什么时候开始或者结束计时，所以可能的最大误差会达到48分钟。48分钟相对于365.2天这么长的时间，倒也不大，不过我们当然想获得更加精确的测量结果了，而这就需要更多次的测量了。不过，我们先不急着测量，我们还是回到原来的目标上，因为在这一年的观测中，我们已经建立起了模型，也已经具备了推测这一年地球上任何地点任意时刻的太阳方位的能力，所以我们不妨先获得这一年的研究成果，再去考虑需要花更长时间的测量。另外，我们在画星图的过程中也在北纬40°地区观测了这一年内每天太阳的方位变化，我们到时候可以对比模型给出的结果和实际观测结果，看我们的推测对不对。

§3-3 用模型推测一个地点的观测结果

§ 3-3-1 太阳方位变化

由于我们是站在地面，感受不到地球的转动或者进动，因此我们现在要对之前的模型进行一个调整，我们要将所有地球的运动转化为天球的运动。

首先，自转很好解决，我们让地球停止转动，然后让天球反方向转动就可以了。至于地球的进动，我们之前说过需要三年才能察觉到，因此，我们不妨先不考虑这一项。这样，我们就得到了一个新的模型：地球静止，太阳在天球上以将近365.2天运转一周的速度在黄道上运行的同时，天球绕着天轴（为了区分，我们叫天球转动所绕的轴为天轴，叫地球转动所绕的轴为地轴，实际上它们是重合的）以23小时56分钟4秒转动一周的转速旋转，如图3-3（a）所示。

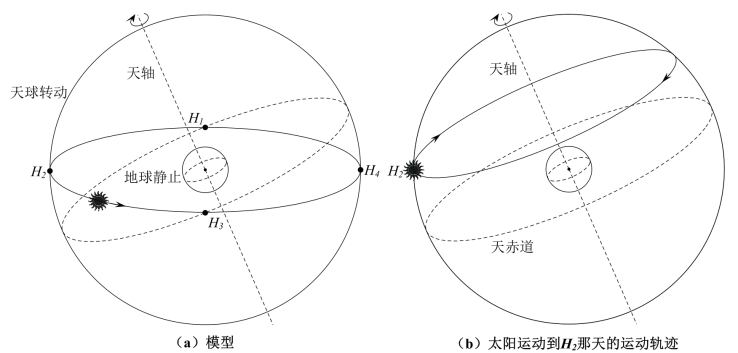
图3-3

由于太阳在黄道上的运行速度很慢，因此，当太阳处于天球上任意一点时，这个点对应的恒星旋转规律就可以近似作为这天太阳的运动规律。比如在图3-3（b）中，当太阳运动到H2点时，这天太阳随着天球转动的轨迹就是平行于天赤道的轨迹。现在，假如地球上任何地点的人都可以看穿地面，那么他们看到的太阳轨迹将会是一模一样的。我们再考虑一下地面对他们视线阻挡方向的不同，太阳在地球上任一点的方位变化在原则上就全都出来了。

具体来说，我们可以这样做：如图3-4所示，我们可以在地球上随便挑一个点，然后把整个旋转的天球（包括在天球上移动的太阳）缩小为一个投影球，接着将这个投影球平移到这个点的地面，让其一半处于地下，一般处于地上。在这之后，这个投影球上的太阳就会时刻保持和天空中的太阳重合，我们就可以把握太阳的方位变化规律了。

图3-4是以北纬40°的某一点O为例子绘制的，但实际上，对于地球上任何一个点都可以进行完全一样的操作，所以我们已经可以给出地球上任何一个地点的观测结果了。当然，这些都是原则上的，我们还要进一步研究太阳具体是怎么运动的。我们就以O点为例研究，并且检验模型给出的结果是否和观测结果吻合。

图3-4

接下来，为了让O地的地面水平，我们要把图3-4逆时针转上一定的度数，然后把视野拉近到投影球，并且再画出一个水平的圆弧分出地上和地下，这样就得到了图3-5：

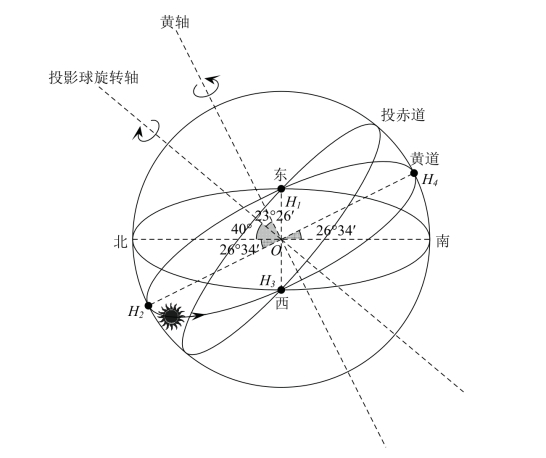
图3-5

由图可以知道这个转动的角度为26°34′。现在，我们用这样一个图像来推测太阳在一天中的运动情况。我们先来考察太阳在一个周期中分别运动到H1、H2、H3、 H4这4个特殊点时对应的一天当中的运动规律，然后寻求太阳运动到其他任意点时的规律。

H1点：将图3-5中的OH1线段绕着投影球旋转轴转动一周就得到了太阳在这天的运动轨迹，这个轨迹实际上是和投赤道重合的，如图3-6所示。

从图3-6可以看到，太阳从正东方升起，以偏南方的弧线越升越高，到达最高点M后开始降低高度，然后往偏北的方向以对称的弧线落下，直到从正西方落下。由于晚上看不到太阳，因此，就不考虑地下部分的太阳轨迹了。

我们注意到，这天日出和日落分别在正东和正西方，并且还有一个点会引起我们的注意，那就是太阳达到最高点M时。很容易知道M点处于正南方，且根据图中的几何关系可以算出这一点的高度角为50°。我们称太阳升到最高点M的时候是日中。这样，一天之中太阳的运动轨迹一方面可以精确地由绕轴运动表示出来，另一方面可以由日出、日中、日落三个点以及三点夹的两段对称弧线粗略但又直观地表示出来。这一天的太阳运动轨迹和我们观测到的结果是完全一样的。

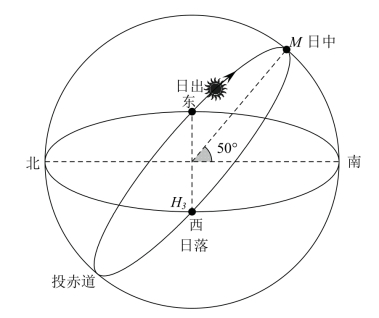
图3-6

H2点：过了近92.7天，太阳从H1点移动到了H2点，H2点是最为偏离投赤道的位置之一，也就意味着它升起和落下的位置是最为偏离东西方向的。我们可以通过OH2线段的绕轴转动得到太阳扫出的轨迹，或者我们只要过H2点做一个平行于投赤道的轨迹就可以了。最终我们得到图3-7所示的图案。

这次，我们只画了地上的太阳运动轨迹。可以看出，这次太阳已经不是从正东方升起了，日出点相比正东方偏北一定的度数，这个度数是31°16′，它完全可以根据几何关系计算出来^[1]。太阳在日出后仍然以一个偏南的弧线升起，直到达到最高点日中后又从偏北的弧线落下，直至日落。这两段弧线是对称的，所以我们可以知道日落的位置在西偏北31°16′。日中时，太阳依旧在正南方，且此时的太阳高度角可以根据几何关系计算出来为73°26′。这样，这天的太阳运动轨迹就出来了，和我们观测到的结果也是吻合的。

H3点：又过了近93.6天，太阳渐渐在黄道上从H2点运动到点H3。将OH3绕投影球旋转轴转动一周后的轨迹是和OH1绕轴旋转一周的轨迹一模一样的，所以太阳在H3点这天的运动情况是和其在H1点一模一样的：日出日落分别在正东和正西，日中高度角50°。

H4点：又过了近89.0天，太阳从H3点移动到了H4点，这又是最为偏离投赤道的位置。仍然将OH4绕投影球旋转轴旋转一周，或者过H4作平行于投赤道的轨迹，我们得到图3-8。

同样的，太阳在空中划出对称的弧线，我们仍然关心日出、日中、日落这3个关键的节点。此时日出日落已经不在正东方了，而是比正东和正西都偏南了，且偏离的角度都仍然是31°16′。日中时，太阳依旧在正南方，但高度角减小为26°34′。日出、日中、日落3个点确定后，太阳的运动轨迹就基本确定了。这一天的情形和我们的观测结果也是吻合的。

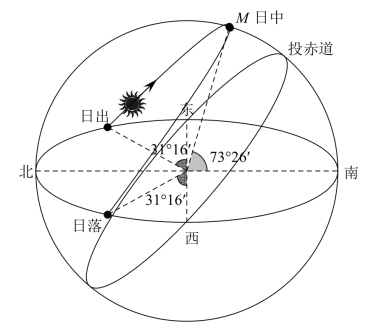
图3-7

图3-8

过了近89.9天后，太阳又会回到H1点。

上面只是给了一个周期中的4天的太阳运动轨迹，但实际上，任何一天的情形都可以通过完全一样的方式来获得。不过，其实我们可以通过另外一种方式，即过渡的方式获得每一天的情形。为此，我们先把这特殊的4天的太阳运动轨迹画下来，并且去掉地下的投影球，得到图3-9。

图3-9

在图3-9中，轨迹2（和投赤道重合）是太阳处于H1、H3点那天的运动轨迹；轨迹1是太阳处于H2点那天的运动轨迹；轨迹3是太阳处于H4点那天的运动轨迹。我们现在先考虑这个问题：从H1点到H2点的这些天中，太阳的运动轨迹是怎样的呢？

考虑到每天观察到的太阳运动轨迹都要垂直于投影球旋转轴（或平行于投赤道），你可以想象轨迹2沿着投影球旋转轴的方向往轨迹1的方向平移，并且平移的过程会同时放大直到正好可以和投影球相交，那么在移动过程中的轨迹就是太阳从H1到H2的这些天中的运动轨迹了，如图3-10所示。

图3-10

这些轨迹的一些特性是，日出和日落方向都渐渐往北移动，且日中时高度角越升越高。以此类推，将轨迹1沿着旋转轴平移至轨迹2，途中生成的轨迹就是从H2到H1这些天内太阳的运动轨迹了。轨迹2到轨迹3或者轨迹3到轨迹2的过渡也是一个道理。而这些推测的结果都和我们观测的结果相吻合。

现在一切都显得非常明了了，但是我们一直都只顾着考虑太阳在天空中划过轨迹是什么样的，而忽略了太阳在这些轨迹上的运动随时间的变化。不过你可能会觉得这太简单了，我们已经知道了投影球的旋转是匀速的，那方位就是匀速变化的了，那这个问题就解决了。实际上，为了简单起见，我们一直忽略了每天太阳在星图上将近1°的移动，而这1°的忽略会带来微小的误差，我们不妨来估算一下：如果我们忽略太阳在星图上将近1°的移动，那么太阳就相当于恒星，一天中绕旋转轴转动一周所花的时间就是23小时56分4秒。但是由于这1°的存在，因此，我们应该少算了（因为太阳往投影球旋转的反方向运动）23小时56分4秒的1/360，也就是4分钟左右。考虑到白天只有半度左右的移动，也就2分钟，也不是很大，所以作为某种近似还是可以的。另外，一方面，太阳在星图上的运动其实并不是严格匀速的；另一方面，其运动方向还不是和投影球旋转方向重合，所以按理每天的差别也不一样。

我们还会发现，并不是每天白天的时长都和夜晚的时长一样。由于太阳绕着旋转轴做近似匀速的转动，因此，太阳在地上部分绕轴转动的角度越大，就意味着这天的白天时长越长；太阳在地下部分绕轴转动的角度越大，就意味着这天的夜晚时长越长。从轨迹3到轨迹2到轨迹1，太阳在地上绕轴转动的角度越来越大，在地下绕轴转动的角度越来越小（因为地上和地下的角度和是360°不变，所以地上多了地下自然就少了），也就意味着白天的时长越来越长，夜晚的时长越来越短。其中，轨迹1的白天时长最长，夜晚时长最短；轨迹3的白天时长最短，夜晚时长最长。只有轨迹2的白天时长和夜晚时长相等。

当然，前面有关时间的讨论也是和我们观测的结果相吻合的。

§ 3-3-2 太阳对于该地气候影响的分析

这样，我们用模型给出的O地太阳方位变化就和我们观测到的结果相吻合了。另外，在这一年中，我们还同时感受了O地气候的变化，我们不妨分析一下这一年中的太阳到底是怎样影响气候的。

我们仍然使用图3-9帮助我们分析。在图3-9中，从轨迹1到轨迹3，太阳的平均高度逐渐降低，由此我们可以猜测，其对应的气温也会逐渐降低，理由如下：日出和日落时太阳高度低，太阳光柔和；日中时太阳高度高，太阳光强烈。可见太阳高度越高，太阳光越强烈。由此，我们就可以推测，在一年中，太阳“平均高度”越高的日子里，太阳光应该越强烈，气温就应该越高；太阳平均高度越低的日子里，太阳光应该越柔和，气温就应该越低。那也就意味着，轨迹1对应的那天气温应该是最高的，而轨迹3对应的那天气温应该是最低的。

但实际观测结果并不是这样的！虽然轨迹1对应的那天是夏天，气温较高，但是它并不是一年中气温最高的时候！我们发现一年中气温最高的时候出现在太阳从轨迹1运动到轨迹2的一些日子里。同样的，虽然轨迹3对应的那天是冬天，气温较低，但是它并不是一年中气温最低的时候。我们发现一年中气温最低的时候出现在太阳从轨迹3运动到轨迹2的一些日子里。

想来我们之前的推理太武断了。太阳光强烈程度和温度高低并不画等号啊！就拿一天中的情形来说，你会发现在日中的时候，虽然太阳光是最强烈的，但这时候并不是一天中气温最高的时候！一天中气温最高的时候往往出现在日中往后的一两个小时里。所以其实我们之前忽略了一点，温度的升高是需要积累的。我们就考虑这样一个例子：假如你用火烧水，你慢慢将火调大，达到最大后再慢慢调低。你会发现，水最烫的时候其实不是出现在火最大的时候，而是出现在火从最大调低的一小段过程中，因为在这个过程中，只要火焰没有被调到非常低，它给水加热的速度仍然大于水散热的速度，那么温度仍然在升高!

所以现在我们就知道怎么更好地描述一年中太阳对于O地气候的影响了：当太阳的平均高度越高的时候，它对于地面的加热效率越高；当太阳的平均高度越低的时候，它对于地面的加热效率越低。

我们现在就可以想象，当太阳在轨迹1和轨迹3之间来回移动的时候，相当于地下有个火炉，其火焰的强度在来回地调低和调高。而地面温度变化对于火焰强度变化的反应因为需要加热时间累积所以会有个延迟。在这样的假设下，我们再给出两个临界点，如图3-11所示。

在图3-11中，假如分界线1对应的那天是一年中最热的一天，而分界线2对应的那天是一年中最冷的一天，那么这两个分界线就分别是气温从热到冷和从冷到热的临界点，从而我们就可以这样描述一年之中气候的变化：太阳从轨迹2开始往左运动到轨迹1的过程中，气温在逐渐升高；从轨迹1回头往右运动到分界线1的过程中，气温继续升高直至最高；从分界线1一直往右运动到轨迹3的过程中，气温一直在减低；从轨迹3回头往左运动到分界线2的过程中，气温继续减低直到最低；而后运动回轨迹2，气温逐渐升高。这样就完成了一个周期了。或者我们简单点描述：太阳从分界线1一直往右运动到轨迹3又回头移动到分界线2的过程中，气温一直在减低；太阳从分界线2一直往左运动到轨迹1又回头移动到分界线1的过程中，气温一直在升高。

不过，其实从一直以来的经验来看，一年中的气温变化并不严格像我们描述的一样分成两段，一段增温一段降温。气温总是存在波动的，尤其在冬天，这样的波动最明显，比如我们经常听到天气预报说“冷空气南下”，然后就突然变得很冷，而一段时间后气温又会回升。不过，总体来讲，气温是“波动着”朝着我们所说的大方向前进的，这说明太阳是影响气温的主要原因，但不是所有原因。

图3-11

§3-4 用模型推测全球的观测结果

§ 3-4-1 太阳方位变化

在前面，我只是以北纬40°的观测点O作为例子，来考虑如何由模型获得准确的观测结果。其他地区的太阳方位变化规律是可以按完全一样的步骤给出来的，所以我们对于地球上的任一点的太阳运动情况原则上都已经出来了，只剩下我们去检验了。不过让人感觉非常不舒服的一点是，虽然原则上我们都把握了整个地球上对于太阳的观测结果，但是还是觉得不直观，因为好像为了获得任何一点的观测结果，我们都要进行一番上面的复杂推导过程。为了让其直观，我们可以将推导过程转换成这个思维：只要根据一个地点的纬度，将前面的投影球（包括球上的星图，黄道等）连同其旋转轴变化一下和地面的角度，然后用旋转规律推导就可以了。不过，我还是觉得不够直观，问题出在我们老是想得到准确定量的观测结果，以至于对于整体的定性把握不够好。我们接下来要整体地把握整个地球上不同点的观测结果，以期获得十分直观的理解。

要想获得直观性还是离不开模型的使用。我们前面已经有模型了，不过当我们尝试了以后，我们决定使用地球自转、太阳在天球黄道上运行的模型（如图3-12所示）。然后，我们考虑地球上任何一个地点观测太阳会在哪个方位。

图3-12

我们之前说过，由于地球上任意两个点同时观测太阳的时候，其方位都是平行的，也就是说，对于地球，太阳发出的光是平行光；因此，实际上只要我们掌握了太阳照射在地球上的一条光线，就掌握了太阳照射在地球上任何一个地点的光线了。而这条光线我们可以通过直射点来确定出来。

如图3-13所示，一束平行光照在了一个球上，这个球就会有一半是亮的一半是暗的，而在亮半球上的正中间一点，光线是正好和球面垂直的，我们可以叫这个点为直射点。一束平行光打在球面上可以确定出唯一的直射点；而反过来，只要确定了这个直射点在球上的哪里，这束平行光就完全确定了，从而球上的其他地点会看到这束平行光处于哪个方位也完全确定了。所以我们现在只要确定太阳在黄道上的任一点时，照射在地球上的直射点在哪里就可以了。

地球相对整个天球而言就是一个点，而我们在图3-12中将地球画大了，所以你可以想象整个地球被缩放到地心。现在，联结黄道上太阳的位置和地心得到的连线实际上就表示出了太阳发出的光线，这条光线和地球表面的交点就是直射点。非常巧的是：在图3-12中，如果我们把地球放大，大到和天球重合，那么太阳运行到黄道上的任何一个地点就会对应于地球上的一个地点，这个地点实际上就是直射点。也就是说，太阳在H1、H3点的时候，其直射点就在地球的赤道；太阳在H2点的时候，其直射点在赤道偏北的位置，而且我们可以根据地轴和黄轴的夹角知道这个位置对应的纬度是北纬23°26′；太阳在H4点的时候，其直射点在赤道偏南的位置，而且根据对称性我们可以知道这个位置对应的纬度是南纬23°26′。其他位置就是过渡的过程了，从H2点到H4点，直射点从北纬23°26′移动到南纬23°26′；从H4点到H2点，直射点从南纬23°26′移动到北纬23°26′。

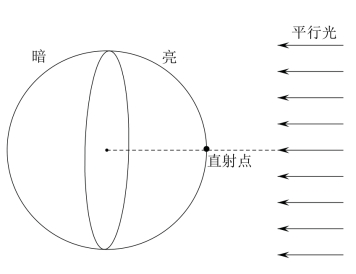
图3-13

不过，你可能会好奇：我只给出了直射点的纬度，没给经度啊！根据模型，地球是自转的，所以随着地球的自转，直射点会在纬线圈上移动，从而我们所说的直射点实际上指的是直射的纬线圈。

那接下来，有了直射点的帮忙，对于全球太阳方位变化的分析就变得很直观了。

图3-14

如图3-14所示，太阳在H1点的这天，其直射点在赤道上，其他位置的太阳光可通过平行确定。太阳光将地球分出了两个半球，这两个半球可以用经过南北极的两条相距180°的经线分割开来。其中，右边一个半球是被太阳照亮的，所以这半球的人会发现他们处于白天。而左边的半球是暗的，所以这半球的人会发现他们处于黑夜。你可以在地球上随便选一个点，并且想象此时地球开始自西向东转动。随着地球的转动，这个点会正好沿着它所处的纬线圈轨迹转动。当它经过图中离我们较近的那条分界线时，它从暗半球进入亮半球并会观察到日出。继续转动，转到距离太阳最近的那条经线时，太阳处于它的子午面上，也就意味着太阳升到最高，这就是日中。继续转，转到离我们较远的那条分界线时，它从亮半球进入暗半球，此时它正经历日落。经过一个晚上，它又会回到图中离我们较近的那条分界线，重复之前的过程。由于地球的自转是匀速的，而且任何一个地点所在的纬线圈都正好是一半处于亮的半球，一半处于暗的半球，因此，我们可以直接推测出，这天地球上任何一个地点的白天和黑夜的时间长度都是一样的。

由上面的分析可以看到，对同纬度的不同地区而言，人们在地球自转时经历的过程是一模一样的，所以以后我们的讨论就以纬度为单位了。接下来，我们比较关心的是每个地区观察到的日出日落的方向以及日中时的高度角。

日出日落：离我们较近的那条交界线正发生着日出，可以看到在这条交界线上的任意一点，太阳光线都和当地的纬线重合，而纬线总是往东西方向延伸的，就说明这些地点观察到的日出方向都是正东。而这些地点包含了所有的纬度地区，也就说明在这一天地球上的任意一个地点观察到的日出方向都在正东。同理，这一天在地球上任何一个地点观察到的日落方向都在正西。

日中时太阳高度角：最右边那条经线上正经历着日中。由于太阳光直射在赤道，因此，在赤道上的人会发现此时太阳正好处于他们头顶，即和地面的夹角是90°。而从赤道往北移动，由于地面在往北弯曲，而太阳方位始终保持平行，因此相对而言，越往北的地区的人就会发现太阳越往正南方移，且和地面高度角越来越小，直到北极点时，这个角度就变为0°了。现在，我们得到的规律就是：赤道纬度为0°，太阳日中高度角为90°；北极点纬度为90°，太阳日中高度角为0°；再考虑到地球的弯曲是相对均匀的，所以我们大致可以判断，如果一个地区的纬度为n°，那么该地区的日中高度角就是90-n°。对比我们之前在北纬40°地区测量到的日中50°的高度角，正好吻合，所以我们觉得这个关系没问题。这里只考虑了从赤道往北的情形，而往南的情形可以完全类似地给出。我们很容易知道，在南半球，除了日中时太阳总是在正北方而非正南方，其他关系是和北半球一样的。

还有两个比较特殊的点我们之前默认不考虑——南极和北极。根据图我们可以推测，在北极点，这一天我们会观察到太阳沿着地平线顺时针移动，也就不存在日出日落或者日中了。之所以我用顺时针的说法，是因为在北极哪个方向都是南方，所以我根本无法用东西南北来描述太阳的移动方向。同理，在南极点，我们也会观察到太阳沿着地平线移动，只不过其运动方向变成逆时针了。

在接下来的日子里，随着太阳在星图上的移动，太阳在地球上的直射点会渐渐北移，所以之前说的情况都有可能发生变化。我们现在来考虑当太阳移动到H2点的那天，即直射点达到最北的北纬23°26′时的情形。

如图3-15所示，太阳的光线仍然将地球分为了亮和暗两个半球，不同的是这次两个半球的交界线不再和经线重合。我们之前说过，由于地球绕着地轴转动，因此，地球上任何一个点其一天中的转动轨迹就是该地的纬线圈。那这样的话，我们首先会观察到一个很有意思的现象：在北极附近有一块区域，其纬线圈是始终处于亮的半球，也就意味着这块区域始终是白天；同理，南极附近也有一块区域，其纬线圈始终处于暗的半球，也就意味着这块区域始终是黑夜。根据几何关系，我们可以具体计算出这两块区域的纬度范围，它们分别是北纬66°34′纬线圈以北的区域和南纬66°34′纬线圈以南的区域。而除了这两块区域，其他地点都存在着白天和黑夜的交替。根据每个地点纬线圈在亮半球和暗半球占据的长度不同，我们可以判断：在赤道地区，白天和黑夜的长度相等，但是从赤道往北，白天的时间长度渐渐增长，晚上的时间长度渐渐变短，直到北纬66°34′的时候，全天都变成白天了；同理，从赤道往南，白天的时间长度渐渐变短，而晚上的时间长度渐渐增长，直到南纬66°34′的时候，全天都变成晚上了。

接下来，我们仍然考虑日出、日落、日中的位置。

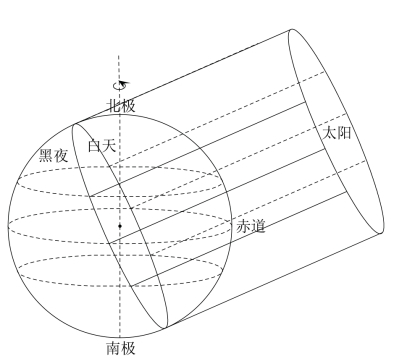
图3-15

我们先考虑日出和日落。在图中靠近我们的这个交界线上正经历着日出，你会看到无论是这个交界线上的哪个点，太阳光线相对于当地纬线都会偏北，也就意味着交界线上的任何一个点都会观察到太阳从东偏北的位置升起。但是这个东偏北的角度在不同的地点是不是一样的呢？光从图来看，我们感觉是这样的，但只要你考虑一下最极端的北纬66°34′的情形，就知道不是这样的，因为这个地点观察到的太阳方位是正北方。仔细思考后我们发现，这些地点的经度不一样，从而它们的纬线向东延伸后并不彼此平行，从而和平行的太阳光的夹角会不一样。实际上，如果你认真分析一下会发现：这个角度在赤道是最小的，且正好是23°26′，并且从赤道往南北方向都逐渐增大，到北纬66°34′和南纬66°34′地区的时候都达到了90°。那现在的情况就是，赤道地区，即0°纬线地区，夹角为23°26′；北纬66°34′和南纬66°34′地区，夹角为90°。那其他地区的夹角会不会是据此线性增加呢？实际上，我们不好判断，因为这不像地球弯曲是均匀的这么容易判定了。不过，通过考虑之前在纬度40°地区得到的31°16′，我们可以判定并不是这样的，因为按照线性增加的规律，在北纬40°地区观察到的角度应该是63°26′而不是31°16′。那现在问题是，既然这个角度的增加不是线性的，那么具体是什么关系呢？我们现在还没能力解决，不过等我们以后学了数学，就可以想办法找到一个公式，以至于我们只要将纬度代进公式一算就能得到夹角。以上考虑的是日出的情形，根据对称性可知日落的情形是一模一样的，只要把东偏北改成西偏北就好了。

接下来，我们考虑日中时的太阳高度角。仍然是最右边的那条（或那两条）经线经历着日中。这个问题其实和之前是一样的，只不过这次太阳的直射点在北纬23°26′地区了。首先我们可以知道，北纬23°26′地区在日中时太阳正好在头顶，达到高度角90°。而从北纬23°26′往北移动，日中时太阳就会往正南方降低高度角，而移动多少纬度，高度角就减低多少度。我们仍然可以用之前在O点得到的角度来验证：从23°26′往北移动16°34′就正好到达北纬40°了，就意味着太阳的高度角降低了16°34′，即变为90°-16°34′=73°26′，和我们之前得到的结果是一模一样的。另外，北纬23°26′以南的地区也是同样的情形，只不过日中时太阳在正北方。这样，日中的问题也解决了。

不过，在这里我们其实还有一个很感兴趣的问题，虽然我们说在北纬66°34′以北的地区全天都能看到太阳，但具体看到的太阳方位变化会是什么样的呢？我们可以考虑这块地区的两个特殊位置：一个是北纬66°34′地区，一个是北极点。首先，我们考虑一下比较简单的北极点。实际上，因为在这个地点地轴正好穿过地面直指头顶，所以如果你垂直竖起一根木棍，你会发现太阳在天空中会绕着这根木棍一直转动，并且一整天的太阳高度角都不会变化。通过图形，我们可以知道这个高度角就是23°26′，就是直射点的纬度。所以其实我们可以判断，在太阳从直射赤道渐渐移动到直射北纬23°26′地区的过程中，在北极观测到的太阳运动情况是：绕着垂直于地面的木棍顺时针螺旋式从地平线渐渐上升直到高度角为23°26′。我们也可以预测，随着太阳在星图上继续移动，在北极点又会看到太阳螺旋式下降直到地平线以下，而后又螺旋上升到地平线，完成一个周期。

我们再考虑一下北纬66°34′地区会观察到怎样的太阳运动情况。此时，这个地区的投影球旋转轴指向北面，高度角为66°34′，一天之中太阳就绕着这个轴转动。太阳转到最低点的时候，正好贴着正北方的地平线扫过，然后又开始升高，达到最高点时处在了正南方向，高度角可以算得为46°52′。看样子，这些特殊地区的太阳运动现象还是相当有意思的。当然，对应的南纬66°34′以南的地区都看不到太阳，也没啥好研究的。

接下来，太阳直射点又开始从北纬23°26′地区渐渐往南移动，直到又开始直射赤道，一切又回到了之前考虑过的第一种情形。太阳直射位置继续往南移动，直到移到最南方的时候直射南纬23°26′，我们来考虑一下这天的情形。

如图3-16所示，现在这个情形除了南北方向的区别，其他都和之前太阳直射北纬23°26′时的情形一模一样。我们很容易通过分析得知，在北纬66°34′以北的地区一整天都是黑夜，而在南纬66°34′以南的地区一整天都是白天。赤道地区白天和黑夜的时间长度都是一样的，而从赤道往北，白天的时间在缩短，黑夜的时间在增长，直到北纬66°34′的时候一整天都是黑夜了。而从赤道往南，白天的时间在增长，晚上的时间在缩短，直到南纬66°34′的时候一整天都是白天了。日出和日落的角度都变为东偏南，且赤道地区正好是东偏南23°26′，往南北方向移动时，这个角度都变大，直到南北纬66°34′时，角度变为90°（正南方）。日中时候，在南纬23°26′太阳高度角正好为90°，往正北方移动的时候，移动多少度，日中太阳就往正南降低多少度，可以计算得北纬40°地区的角度正好是我们之前得到的26°34′。同理，往正南方移动的时候，移动多少度，日中太阳就往正北降低多少度。另外，此时在南纬66°34′以南的区域观察到的太阳和我们之前考虑的北纬66°34′以北地区的太阳运动情况是一模一样的，只是南北方向调换了一下而已。

我们在这里只考虑了特殊的4天地球上不同点观察到的太阳方位变化，其他的日子就是过渡期了。在分析过渡期情形的时候，我们仍然要注意一个关键点，即太阳直射的纬线圈。你可以自己将整个过渡的过程在脑中呈现一下，等你对此很熟练后就会获得很直观的认识，我就不多说了。

§ 3-4-2 对全球气候的猜测

接下来，我们顺便考虑一下气候的问题，推测一下全球的气候是如何变化的。首先，从前面所有的推测我们可以看出，对同一个纬线圈而言，它与太阳之间的相对位置关系都是一样的，所以我们可以推测，如果太阳是引起气候变化的主要原因，那么同一个纬线圈的气候应该都是基本一样的。同时，结合之前我们研究过的北纬40°的某一点O的气候，我们就可以推测在北纬40°的所有地区，气候都是和O点的气候基本相同的。接下来，我们要猜一猜除了北纬40°外，其他纬度地区的气候会是怎样的。

图3-16

由于我们对于O点的气候很了解了，而太阳的位置由其直射点可以完全确定，因此，我们研究的突破口就是观察O点的气候变化和太阳的直射点移动有什么联系，然后运用这个联系来判断太阳在不同直射点时其他点的气候是什么样子的。我们之前对于O点的气候和太阳的关系总结出了一个很有说服力的假设：当太阳的平均高度越高的时候，它对于地面的加热效率越高；当太阳的平均高度越低的时候，它对于地面的加热效率越低。而当太阳的直射点从北纬23°26′移动到南纬23°26′的过程中，在O点的人，会观察到太阳的轨迹渐渐从轨迹1变为轨迹2然后变为轨迹3，即太阳的平均高度渐渐下降。那也就意味着，太阳直射点从北纬23°26′移动到南纬23°26′的过程中，太阳对于O点的加热效率在渐渐降低，由此，我们可以猜测：对一个纬线圈而言，太阳的直射点离这个纬线圈越近，太阳对这个纬线圈的加热效率就越高；太阳直射点离这个纬线圈越远，太阳对这个纬线圈的加热效率就越低。

其实，根据生活的常识，我们会发现这样的假设是相当可信的。就比如冬天的时候，当你在一个火炉旁边暖手时，你会下意识地把手掌张开正对着火炉暖手，而不会“斜斜地”对着火炉，这就说明在直射的情况下我们可以吸收更多热量。当然，火炉毕竟不是太阳，它发出的光不是平行的光。为此我们可以针对太阳来做一个小实验：你站在太阳光下，张开两只手掌，让一只手掌直接朝向太阳，接受太阳的直接照射，让另一只手掌相对太阳“斜斜地”放置，然后你对比一下两只手掌感受到的温热程度。你会发现直接朝向太阳光的手掌会感受到更多热量。

回到地球接受太阳光照射的情形，当太阳光照射在地球上的时候，离直射点越近的纬线圈，它就越是“正对”太阳，感受到的太阳光就应该越强烈；离直射点越远的纬线圈，它就越“倾斜”地对着太阳光，感受到的太阳光就应该越柔和。我们现在就用这样的原理来猜猜全球的气候会是怎样变化的。

首先，我们会想到的一个结论是：太阳的直射点在北纬23°26′和南纬23°26′之间来回移动，那这块地区就始终是离直射点非常近的，也就意味着这块地区的温度肯定是全年都非常高的。我们可以以赤道作为例子，太阳直射点离赤道最远的时候只有23°26′，这比我们在O点和直射点的平均距离40°要小得多，也就是说，赤道地区即使在一年中最冷的时候，也会比我们的春天和秋天热得多。

我们再考虑一下北纬23°26′以北地区的温度。对于这些地区，首先我们会知道它们的季节变化是同步的，因为太阳直射点对这些地区的远近变化是同步的：太阳从北纬23°26′往南移的时候，这些地区和太阳直射点的距离都是增大了，气温总体都往冷的方向变化；太阳从南纬23°26′往北移动的时候，这些地区和太阳直射点的距离都减小了，气温总体都往热的方向变化。然后，我们会发现，无论太阳直射在哪一个点，对这些地区而言，越往北的地区，它和太阳的直射点会越远；越往南的地区，它和太阳的直射点会越近。也就是说，拿任何时候这些地区的气温进行同时比较，南方地区的气温总会比北方地区的气温高。

接下来，我们再考虑一下南半球的情形。其实我们会发现一个很有意思的推论：南半球的气温是完全和北半球的气温相反^[2]的。这是因为，太阳在北纬23°26′和南纬23°26′这对称的区域移动，所以当太阳直射在北纬地区的时候，它离北半球近，离南半球远，也就意味着北半球是夏天的时候，南半球是冬天；当太阳直射在南纬地区的时候，它离南半球近，离北半球远，也就意味着北半球是冬天的时候南半球是夏天。由此，我们可以根据北半球的情况非常容易地确定出南纬23°26′以南地区的气候：这些地区的气候都是同步变化的，且在同一时刻，越往南的地区其温度越低。另外，我们还可以知道，对于南北半球同纬度的两个地区，比如，北纬40°和南纬40°而言，这两个地区的气温是完全对称相反的。

对于全球的气候，我们似乎已经非常了解了。但是等等！不对！我们忽略了白天日照时间对气温的影响！

夏天的时候，太阳直射北半球，那么越往北的地区，其日照时间就越长。我们就面临一个问题了：越往北的地区，虽然它离直射点越远，从而太阳对其加热的效率越低，但是它的日照时间长，从而加热的时间就长啊！那到底是加热效率低占上风还是日照时间长占上风呢？如果说加热效率低占上风，那么从南到北仍然是温度从高到低。但是如果日照时间占上风，北方的温度就会更高！到底是哪种情况呢？我们不知道，这需要实实在在地去检验了。对在南北方都生活过的人而言，其实他已经检验过了，就中国而言，夏天的时候，对南方和北方而言，总体来说是同样炎热的。所以可以看出，日照时间和加热效率基本打了个平手。不过对于较极端的位置，比如北极附近和接近赤道的位置，夏天的时候一个气温很低一个气温很高，可见极端位置加热效率减低导致的影响更为显著。

我们还要考虑一下冬天的情形。冬天的时候，越往北的地区日照时间越短，也就意味着冬天的时候北方不光加热效率低，而且加热的时间还短，所以我们可以很判断，越往北的地区温度是越低的。而同样的，在南北方都生活过的人会明显感受到，冬天的时候南北方温度差异相比夏天大得多——南方温度还可以保持0℃之上的时候，北方可能都降到零下几十度了。

对于南半球，我们也可以同样地考虑，得到的结果和北半球类似：夏天普遍高温，冬天越往南的地区温度越低。

§3-5 对所有猜测的检验

到现在，我们已经将地球上任何地点的太阳方位变化以及气候变化都猜测出来了。不过很神奇的是，虽然这些成果很多，但是它们基于的原理非常简洁：1）它基于在A、C两个遥远的地方确定的太阳在星图上的位置相同，从而得到的太阳光对地球而言是平行光的规律；2）它基于我们在O地观察到的太阳在星图上的移动规律。

不过，你也会发现，除了这些基本原理，在推测过程中，我们也做了些其他假设，比如关于太阳加热效率的假设。虽然说很多假设都是建立在合理的观测现象上，不过说到底总是存在这些可能：1）一些假设是错误的；2）我们在猜测的过程中犯了一些逻辑错误；3）大自然本身就是不讲逻辑的，你拿它没办法。从一直以来的经验来看，大自然还是很讲逻辑的，所以第三项我们基本不考虑。前面两项还是有可能发生的，所以无论如何，我们都要对这些猜测进行检验。

当我们真的去实际检验的时候，我们发现不管我们走到哪里，模型给出的太阳方位变化都十分符合观测结果！对气候而言，我们发现我们对于地球上不同地点的气候预测是相当准确的，不过不是百分之百的吻合。比如，我们发现同纬度沿海地区的气候和内陆地区的气候会有所不同。所以这也就再次说明了，除了太阳这个主要因素，其他的一些因素也会影响气候。不过总体来说，无论是对于太阳的方位变化还是全球气候的预测，我们都取得了相当大的成果！

§3-6 对长时间测量结果的猜测

§ 3-6-1 区分恒星年和回归年

到此为止，我们在太阳的一整年研究中取得了很大的成果。那么接下来还剩下的问题是：我们毕竟只探究了一年的情形，那以后太阳的运动是不是真的都这样呢？这需要更加长期的测量来决定。不过考虑到长期测量要花的时间和精力太大，我们可以先花一些时间对长期测量结果做点猜测，因为毕竟这样的猜测仅仅是想想，成本不高，而如果猜对了会非常有助于指导我们的测量。

首先，我们当然会设想这样一种可能性：太阳会一直在星图上完全一样地运动下去。那你可能就会说了，如果是这样的话，那我们对每一年的分析不就和上面的完全相同了！

其实不是这样的。我们之前忽略了地球的进动！在一年的过程中，或许我们还可以不考虑进动，但是在3年、4年、5年等长时间的情况下我们就要考虑进动了。我们接下来先研究这样一个问题：如果太阳的运动真的是一圈又一圈在星图上进行完全相同的运动，那么在我们新增了对于地球的进动的考虑后，模型的预测会和之前有何不同？我们接下来不妨将它们都加入模型进行考虑。

我们这次其实回到了将进动去除前的模型，即图3-2所示的模型：天球和黄轴静止不动，太阳在黄道上周而复始地运动，并且每一圈的运动都是完全相同的（这是新加的假设），而地球在自转的同时，还会绕着黄轴进动。

首先，我们会注意到的一个问题：当地球进动的时候，H1、H2、H3、H4在星图上的位置是会变化的。这是因为，地球一旦绕着黄轴扫动，地球的倾向就变了，从而天赤道就会发生变动，它和黄道的交点H1、H3就会发生变动，进而引起H2、H4的变动。或者换一种更为直观的说法，由于H2点是地球倾向黄道的那个点，因此，一旦地球倾向变了，H2点的位置就会变，从而其他3个点就也跟着变了。这就引出一个问题，我们之前研究的时候都是以太阳在H1、H2、H3、H4上移动一圈的周期进行研究，而一旦这些点不固定，那还有周期可言吗？我们之前测量到365.2天又意味着什么呢？

我们来研究一下：

如图3-17所示，根据地球的倾斜方向，我们在黄道上定出正对着其倾向的一个点，这个点即H2。假如太阳从这一点出发，在黄道上转上一周，当它又回到H2的时候，实际上地球已经不再倾向H2了，而是倾向于与太阳运动方向相反的一个临近的点。所以实际上在太阳回到H2点的路途中已经经过了地球的新倾向点H2′，而我们之前研究的周期就是太阳从H2运动到H2′的周期。可以看到，这个周期和太阳在星图上运动的周期，即从H2 出发到回到H2的周期是不同的。

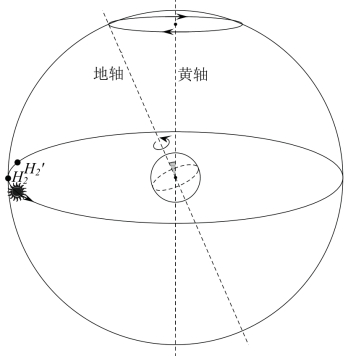
图3-17

太阳在4个H点间的运动周期是太阳和地球的相对关系变化的周期，理应是我们更加关注的周期。而且由于气候变化的周期是太阳在地球上的直射点变化的周期，因此，气候变化的周期也应该是这个周期。为了区分这两个周期，我们不妨把太阳在星图上运动的周期称为恒星年，把太阳在H点间移动的周期称为回归年。我们将这两个周期的差值叫作岁差。可以看出，岁差实际上就是太阳从H2′运动到H2所花的时间。

从这里我们会得出一个推论：回归年是会变化的。因为你想，恒星年是不会变化的，而回归年取决于恒星年和岁差，但是岁差按理是会变化的（理由如下：地球的进动是匀速的，那就意味着每次岁差期间太阳走过的路程都是一样的，但是因为太阳在黄道上的运行速度会变化，所以按理岁差会变化），所以回归年是会变化的。

这个推论其实是很恼人的，因为我们对于“周期”这个词的定义就是一段不变的时间，所以如果回归年会变的话，那它还可以被认为是一个周期吗？令人欣慰的是，近似可以，理由如下：地球的进动是非常缓慢的，每年只有50.29″，也就是说即使过了100年，地球的进动也只有1°左右，而实际上太阳在这1°的轨迹内是非常接近匀速的，所以我们之后如果测量回归年，每年测量到的值肯定是非常接近的。

好了，现在我们就区分出两个周期了：一个是恒星年周期，它是太阳在星图上运动一周的周期；第二个是回归年周期，它是太阳和地球之间相对位置变化的周期，也是地球气候变化的周期。

§ 3-6-2 预测太阳方位的方式的小改动

接下来，我们要考虑在地球进动的情况下如何预测在地球上不同点观测到的太阳方位。我们之前的做法是将所有的地球运动转化为天球运动，我们看看这次这种方法还能否行得通。首先，地球的自转可以转化为天球的反方向转动，这和之前是一样的。但是地球的进动呢？虽然说地球的进动也可以转化为天球整体绕着黄轴的转动，但是这看起来非常麻烦。而这时候非常幸运的是，由于地球的进动和太阳的运动正好都是在绕着黄轴，而且我们这次研究的只是地球和太阳之间的相对关系，并不研究星图上的恒星，因此，我们只要把地球进动的速度加到太阳在黄道上的运行速度（之所以是加不是减，是因为二者转动方向相反），以使得太阳在黄道上运行的恒星年周期变为表征太阳和地球之间相对位置关系的回归年周期就可以了。在这种情况下，我们就可以假定地球不再进动了。

如果你感到费解，你可以想象这样一个实验：假如你和你的朋友在绕着同一个点转动，你是顺时针转动，每秒转动10°，而你的朋友是逆时针转动，每秒转动15°。这时候，还有两个朋友也在玩同一个游戏，但是这两个朋友中一个完全不动，而另一个以每秒10°+15°=25°的速度值逆时针转动，那么在这两个转动的游戏中，你与你朋友之间的相对位置关系和另外两个朋友之间的相对位置关系是一模一样的。

接下来，我们仍然可以将天球缩小为投影球并且放到地球上的任何一个地方，但是唯一不同的一点是，原来天球上太阳运动一周的周期由恒星年变为了回归年。剩下的推导过程可以按照之前的步骤完全一样地进行了。对于气候来说，也是如此。

§ 3-6-3 恒星年和回归年的测量方案

接下来的问题就到了对于恒星年和回归年的测量了。

当然，回归年周期是我们最关注的，因为它是对于太阳方位以及全球气候预测的周期，不过我们先挑简单的恒星年周期来解决。对于恒星年，只要我们测量一下太阳从星图上的某个点出发到重新回到星图上的这个点的时间就可以了。当然，因为白天看不到天上的星星，而我们要用投影球来预测白天天上的星图，所以我们一定要保证在测量的时候投影球星图和天上星图重合。考虑到地球进动影响，如果我们将投影球放在地面连续好几年不调整，我们会发现天上的星图慢慢偏离投影球上的星图。为了让二者再次重合，原则上可以这样：我们把投影球从旋转轴上脱离出来，然后找准一个合适的位置再插入旋转轴，使得天空中的星星和投影球上的星星重合就好了。这样，我们边调整边绘制太阳轨迹，就可以测量到恒星年的周期了。当然，你可能觉得完全没必要那么麻烦，我们只要在相隔很长时间的情况下测量太阳从某一颗恒星出发到又回到这颗恒星的时间，然后将其除以太阳转动的圈数就可以了，并不需要理会这之间太阳的移动。

下一个问题是：如何在地球上测量回归年的周期呢？

原则上可以这样：我们在地球上任意点放下一个没有星图，完全空白的投影球。然后我们将投影球按照地球的自转速度同步地转动，就这样一直转动下去，不管转动多少年都不考虑什么调整的问题。然后我们在这个投影球上描下每天看到的太阳，经过一段时间的描点，我们理应发现这些点形成了一个封闭的圆，这段时间就是回归年的周期。我们继续让投影球转动继续描点，如果我们发现不管转动多少年，太阳描下的点仍然在这个封闭的圆上，我们就可以多次测量它的周期取平均值获得较为精确的回归年周期。当然，你还会说，没必要那么麻烦，我们可以在投影球上画一个投赤道，那么一旦太阳运动到了投赤道上，就表明这一时刻太阳运动到了H2点或者H3点，接下来我们根本就不要转动球，当太阳的方位和这个投赤道再次重合的时候，就说明过了半个回归年了，再下一次重合就过了一个回归年了。我们可以测量好几次的时间总长并取平均值获得更加精确的回归年周期。

§3-7 对于猜测的检验及实际的测量

这样的猜测出来后，原来的探索现在就变成了检验猜测了。那么怎么检验呢？实际上，所有的检验都可以通过上面的测量恒星年和回归年的过程来完成，只不过我们在测量的过程中不能只关注计时开始和结束的时候，而要考虑整个过程。

首先，我们在测量恒星年的过程中要检验太阳在星图上是不是真的进行着一圈又一圈完全相同的运动，并且每次测量到的恒星年周期是不是都和平均值相差不到48分钟。然后我们可以通过测量回归年中所说的观测结果来检验我们对于进动转化为太阳的运动速度变化是不是成立，并且每次测量到的回归年周期是不是都和平均值相差不到48分钟。

通过长期的测量，我们发现观测结果和我们的预测是完全一致的，并且得到恒星年的周期为365日6小时9分9.5秒，或者说是365.25636天。回归年周期为365日5时48分46秒，或者说是365.2422天。后者比前者短了20分钟左右，这个差值就是我们之前说的岁差。由于岁差来源于地球的进动，因此，地球进动的速度一定和岁差的数值有关。我们可以来计算一下：地球的进动为每年50.29″左右，是黄道一周360°的25 770分之一，而太阳在黄道上转动一周需要365天，那么它在地球进动区域的运动时间就是365天的25770分之一，即20分钟左右，和刚刚说的岁差是吻合的，也就让这两个周期的测量结果更加可信了。

§3-8 应用

§ 3-8-1 制定从零开始建立时间体系的目标

就像我们之前将恒星的运动规律应用到绘制世界地图一样，太阳的运动规律也给了我们非常多的应用，其中最大的一个应用是我们现在使用的时间体系，即描述某一个时间点所用的某年某月某日某时某分某秒。其实，如果你仔细分析一下我们使用的时间体系，你会发现许多优点：

1. 每天都是一个白昼的交替，很符合我们的作息，所以即使你不翻日历都可以大致知道过了几天。

2. 一天中的几点是和一天中的太阳运动情况联系起来的：12点时，太阳达到日中，而12点之前的早上是太阳升起的阶段，12点之后的下午是太阳落下的阶段。

3. 每年都是一个气候变化周期的交替，从而每年的月份都和当月的气候有联系，比如每年七八月总是最热的，每年的一二月总是最冷等。这样的历法可以提醒我们气候的变化，同时有利于指导农民的耕种。

现在，我们要根据掌握的太阳运动规律，从零开始建立起这一整个时间体系，并且探索：为什么这样的时间体系会有如此多的优点，又或者为了达到这些优点，我们该如何自己建立起这样的时间体系呢？

我们采取的方案是：先根据在地球上一个地点观察到的太阳运动情况建立起当地的时间体系，然后从这一个地点得到的经验出发，给出其他地点的时间体系，最终进行全球整体的统一。

§ 3-8-2 日晷对一天时长及时刻划分的参考

首先，我们来考虑一天。我们想要的一天是一个昼夜，并且还要根据太阳的运动情况划分时刻。这样的话，一方面我们要搞懂一天有多长，另一方面要适当划分时刻，而我们想要的效果是可以通过日晷表达出来的：

图3-18　日晷的制作

如图3-18（a）所示，我们拿出一根针，将针指向北天极，使得这根针可以作为投影球旋转轴。我们再拿出一个圆盘，令针穿过圆盘圆心，并令圆盘垂直于针，这样圆盘的位置也定了^[3]。现在，由于这根针相当于投影球旋转轴，因此，每天太阳就会近似匀速地绕着这根针旋转^[4]，针的影子就会被投射于圆盘，并且会在圆盘上近似匀速地转动，从而就可以作为一个天然的“钟表指针”了。接下来，我们只要在圆盘上适当地等分时刻，就做成了一个天然的“钟表”了。

日中的时候，影子在正北方，我们在圆盘的正北方向画一条线段（虽然这条线段在圆盘上是往下斜的）并标记为12时；我们在12时的反方向，即正南方向画一条线段并标记为0时（或24时）；我们在正西方向画一条线段，并标记为6时；我们在正东方向画一条线段，并标记为18时。4个主要的时刻定了，其他时刻根据等分就可以定下，如图3-18（b）^[5]所示。

不过这时候你会可能会问：“为什么我们要选择午夜作为日期变更的时候呢？为什么不选取日出的时候为0点呢？”

这是因为日出的方向是在东偏南到东偏北变化的，也就意味着日出时太阳的影子不总是指向一个方向，所以我们没办法在圆盘上定下一个位置。你可能还会问：“既然如此应该选取日中的时候为0点啊，因为日中的时候太阳总是在正南方（对于北半球大多数地区而言），从而影子总是在正北方啊！”

原则上是这样的，只不过我们要是在大中午把日期拨过一天，就太不符合作息规律了，所以我们选择在中午对面的午夜进行日期变更，并定为0时。

制作完了日晷，接下来，我们做什么呢？我们要对照着日晷做一个钟表。你可能会问：“日晷本身不就是钟表吗？为什么还要再做一个？”这是因为日晷有诸多缺点，比如，日晷只能放在户外，在白天、晴天时使用，而且携带不方便。还有一个根本的原因是，严格来说日晷的运行其实并不是匀速的。

我们以前就说过，由于太阳在黄道上的运行并不匀速，且黄道和天赤道还有一个夹角，所以太阳在天空中运转一周的时间是会变化的，也意味着以日晷定出的一天时长会发生变化；甚至在一天内的不同时候，用日晷定出的一小时时长都会有所不同。而钟表不存在这样的问题。

其实，我引出日晷的目的在于指导我们制作钟表，因为日晷是和太阳方位紧密结合的，所以我们只要做一个和日晷几乎同步的钟表，这个钟表就也会和太阳方位紧密结合。而为了实现这一点，我们可能会这样做：我们在某天日中的时候用一个钟表（注意：这个初始的钟表不使用小时或者分钟作为单位，因为我们还不知道一天有多长！）开始计时，到下一次日中的时候停止计时，根据这段时长就可以给出一天的长度，从而确定出钟表运行的速度。我们再将钟表拨至和日晷同刻度的位置，接下来钟表的示数就会和日晷的示数同步了。但是问题在于，由于日晷给出的一天时长会变化，因此，过了一段时间后，随着误差积累，钟表的示数可能会明显偏离日晷的示数，我们就又不得不调整钟表了。其实，重点在于，我们究竟该确定钟表运行速度为多大，或者更直接地说，我们要定一天或一小时的时间为多长，才可以让它保持长时间和日晷示数近似相同而不用调整呢？可以看到，让二者长时间同步才是我们要解决的重点！

§ 3-8-3 确定钟表的运行速度

为了解决这个问题，我们引入了平太阳模型。图3-19是之前的投影球。我们这样想象：当太阳从H1点出发沿着黄道前行时，有一个平太阳同时从H1点出发，但是沿着投赤道前行。太阳在黄道上运行一周的时间是回归年的长度，而我们规定平太阳在投赤道上运行一周的时间也是回归年的长度，那么我们可以知道，一个回归年后平太阳和真太阳又会同时回到H1点。如此一来，它们就一直从H1点出发然后又同时回到H1碰头，周而复始。但是有一个很重要的不同点是，太阳的运动是不匀速的，而我们规定平太阳的运动是匀速的。

现在，我们要对平太阳每天相对于地面的方位变化进行分析。由于平太阳一直处于投赤道上，因此，平太阳每天在天空中扫过的轨迹都会和投赤道重合，永远不变。而且由于平太阳相对星图在投赤道上是匀速运行的，因此，平太阳每天在轨迹上的运动也是完全匀速的。结合轨迹不变与速度不变，我们可以推出：如果我们用一个日晷来给平太阳进行投影并计时，则给出的每天时间长度、每小时时间长度等都是一样的！

那问题就在于，如果现在有两个日晷，一个记录平太阳的时刻，另一个记录真太阳的时刻，那这两个时刻会很接近吗？如果很接近，我们就可以用平太阳的时刻代替真太阳的时刻，从而就同时保持匀速和与太阳方位结合两个优良特性了！

实际上你会发现，由于平太阳和真太阳的周期都是回归年，且两个太阳的轨道很接近，因此，无论它们在各自的轨道上运行多少圈，两者都会保持很靠近。那也就意味着，它们会在很小的时间间隔内分别日中，而日中的时间一旦接近，其他时刻由于一天中地球自转占主导地位从而就基本相同了。

你可能会问：“难道我们真的要做一个缩小的道具来模拟平太阳和真太阳的运动吗？”

不需要的，这些都是假想的。只要我们根据这些假想确定出一天或一小时的时长有多长，然后根据这个时长制作出钟表就行了。那我们该怎么确定这些时长呢？

我们现在不能用之前的小时、分、秒等单位，因为这些正是我们现在需要测量的时间长度。那我们用什么单位呢？有很多种选择。打个比方，我们做一个水钟，并令一滴水从1米高处落下的时间为单位来计时，并且把这个单位叫作一水滴。我们首先用这个水钟测量投影球转动一周的时间长度（即地球自转周期），假设我们发现是n水滴。然后，我们测量平太阳在投影球上运行一周的时间长度（即回归年长度），假设我们发现是m水滴。现在，我们要确定一天时长该定为多少水滴（接下来的推导涉及一些数学，如果你觉得看不懂没关系，只要知道通过m和n可以确定一天时长就可以了）：由于在n水滴时间内，投影球转动了360°，那么在一水滴时间内转动的度数就是360°/ n ；同理，由于在m水滴时间内平太阳在投影球上移动了360°，那么在一水滴时间内移动的度数就是360°/m。接下来，投影球带动平太阳每水滴转动360°/ n的同时，平太阳会在投影球上往反方向每水滴移动360°/m，因此，平太阳真正转动的度数为每水滴360°/n-360°/m。那要花多少水滴时间才能转过360°呢？答案是360°/（360°/n-360°/m），这个时间就是我们定出来的一天时长了。

图3-19

我们将这一天时长等分为24份，叫每份为一小时；再将每小时等分为60份，叫每份为一分钟；再将每分钟等分为60份，叫每份为一秒钟。所以一秒钟这个单位就是这么来的，我已经解答了在§2-4中遗留的问题。

知道了该定钟表的运行速度为多少，我们只要合理调整初始时刻，在这以后钟表就会一直指示着平太阳的时刻，从而就和真太阳的时刻非常接近了。

§ 3-8-4 闰秒的产生

即使到了21世纪，每天使用的几时几分几秒等仍然是根据之前的原理设定的，不过，我们比较高科技了，我们用的是原子钟计时，然后授时给其他仪器。但这里就产生一个问题了，我们说过地球自转会相对于原子钟变慢，这就会使得我们所定义的一天时长会变长！

为什么呢？地球自转速度的减慢，会导致太阳绕着旋转轴转动一周的时间变长，那一天的长度自然会变长了！这就意味着，我们以平太阳制作的日晷，其针影在圆盘上转动的速度其实会渐渐变慢！

现在，我们冷静冷静分析一下问题：我们想象手上戴了两个表，一个叫作“日晷”，另一个叫作“原子钟”。在“日晷”的表盘上，指针转动的速度会越来越慢，而在“原子钟”的表盘上，指针转动的速度为匀速^[6]。当这两个钟表开始同时转动的时候，我们会发现“日晷”越来越落后于“原子钟”。而现在的问题是，我们平时只看“原子钟”这个表，但是想要得到的却是“日晷”这个表的示数，那该怎么办呢？

我们采取这样一个方法：当我们发现“原子钟”上的示数比“日晷”的示数多一秒的时候，我们把“原子钟”暂停一秒（或加一个无用秒，比如第60秒），给“日晷”一秒钟时间赶上，然后再继续计时。反映到真实的日晷和原子钟，这多出来的一秒就叫作闰秒。

那闰秒多长时间加一次呢？我们发现，有时候一年就要加一次，有时候过两三年都不用加，这说明地球自转不是匀速减慢的。

从闰秒的引入可以看到，虽然我们希望钟表可以长时间不用调整，但我们仍然做不到完全不需要调整。当然，也有人建议放弃钟表时刻和太阳的对应关系，如此一来就不用引进闰秒了，因为其实要让全球钟表拖延1秒并不是件容易的事。但这样的话，按经验大致推算，七八千年后日中的时刻都要到下午两点多了，这会是我们想要的结果吗？还有比较折中的方案是不要差1秒就调整，差个一两分钟再调整也行，如此一来就是1世纪1次的问题了。对于这些人为规定的问题，我们就不深入研究了。

另外还有一个问题是，既然一天的时间长度会发生变化，那么按照定义，1小时、1分钟、1秒钟的时间长度也会发生变化，那我们要不要去修改这些单位对应的时间长度呢？

如果我们希望24小时始终是一个昼夜，那么秒（包括小时、分）的定义还是要改的。但问题是，我们对于这个单位早就用习惯了，并不想改^[7]。所以考虑到短期内地球自转速度变化不大，我们可以暂时不改，而且为了让秒是一个特定的长度不变，我们还要依据原子钟的原理来重新定义秒：我们定义1秒为铯133原子基态的超精细能阶间跃迁时所辐射电磁波周期的9 192 631 770倍^[8]。如此一来，秒这个单位就依附于原子钟而不依附于地球自转，也就不存在发生变化的问题了。

§ 3-8-5 公历的建立

有了一个调好时间的钟表计时后，我们现在完全可以这样计日：第一天、第二天、第三天……完全不需要年月。那年月拿来干什么呢？有的人可能会说，就像我们的长度单位，其实只要有了米这个单位就可以进行测量了，而之所以还搞出千米这样的单位，是为了让长距离的表达更方便，那年月的出现也只是为了让长时间的表达更方便。但问题是，如果只有这个原因，我们完全可以定10天为1个月，10个月为1年……

先不说月份，年份的出现主要是为了利用起四季更替这个自然周期，这样每一年都是一个四季的变化，和一天是一个昼夜一样，非常有利于我们的作息和计数。

首先遇到的一个问题是，我们肯定希望一年的长度是整数天数，但四季更替的周期是回归年周期365.2422天，并不是整数。那该怎么办呢？我们有解决方案：我们有时候让一年是365天，有时候让一年是366天，而在长时间的过程中让其平均值稳定在365.2422天。那现在的问题就是：什么时候让一年是365天，什么时候让一年是366天呢？我们来解决这个问题：

如果前4年都以365天为1年，那么这4年我们就少算了4×0.2422=0.9688天，为此，我们在第4年补上1天。这样，第1、2、3年是365天（我们称之为平年），第4年是366天（我们称之为闰年）。但是在4年中，我们又多算了1-0.9688=0.0312天，如果我们不顾这样的误差一直按照每四年一闰的规律计算，过了100个这样的4年，即400年后就会多算出100×0.0312=3.12天，所以我们还要在这400年内减去3天。那我们就在第100、200、300年扣去1天，而这3年本来都是闰年366天，扣去1天就都变成平年365天了。那也就是说，每400年中，除了第400年保持闰年，前面整百的年数不再是闰年。现在这400年还多算了3.12-3=0.12天，如果以后都以这样的400年为单位重复，要过10个400年，即4000年后，误差才会有1.2天。由于这个时间太久远，而且到那时候可能回归年的长度已经有明显变化了，因此，我们暂且不管了。

为了方便，在1年之内我们还分出了月。公历中将1年分为12个月：1月31天，2月28天（闰年29天），3月31天，4月30天，5月31天，6月30天，7月31天，8月31天，9月30天，10月31天，11月30天，12月31天。这样总共合起来，平年就是365天，闰年就是366天。其实这个月份的划定带有人为和历史因素，它本质上和月亮无关^[9]。

我们定下了公历的体系，只要再定下某天为第一年第一月第一日，以后任一天是哪年哪月哪日就完全确定了。至于公元1年1月1日该设为哪天，其实带有任意性，不过我们已经设定好了，并且据说这天是耶稣生日。但是毕竟年代有点久远，我们不知道当时设定这个日子的人是否真想按照耶稣生日进行设定，而即使他想这么设定，他有没有搞清楚耶稣生日是哪一天也是个问题。不过可以确定的是，并不是说从公元1年1月1日那天就开始施行公历了，我们仅仅是把那天放在历史上的某一天而已。那公历最早什么时候开始实施呢？这是历史问题了，不是我们研究的重点。

如此一来，我们就制定好了一个可以指示气候变化的历法，非常符合我们的作息。不过，它有一个小小的缺点：一年有时候是365天有时候是366天，一个月从28天到31天都有，所以如果你想用年或月表达一段时间，你很难说得十分准确。当然，我们也可以约定一下，比如我们约定当用年表示一段时间时指的是365.2422天，这样会准确一些。不过大多数情况下，如果我们要用这么大的单位表达时间，其实也不是很在乎这一两天的区别，又或者我们总是指定一些特定的年份或月份，而这些年份或月份的时长是确定的。

§ 3-8-6 公历和阳历的区别

回顾公历的制定，可以看到其中有很多任意项。比如一年定为几个月，一个月定为几天，四年一闰中该定哪一年为闰年，百年不闰四百年再闰中又该定哪一年为再闰，还有以哪一天作为公历的起点，等等。在这些任意项中，即使我们选择不同的选项定历法，得到的历法也是和四季相协调的。或者我们完全可以不按四年一闰、四百年再闰这样的方法，我们还可以想出其他的方法制定闰年……所以这里就有必要说说阳历和公历的区别了。

凡是以太阳运动周期为基础制定的历法都叫阳历，它都可以指示气候的变换。公历是一种阳历，它选择了我们之前所说的任意项选项，而如果我们选择其他的选项就形成了另外一种阳历，但不叫公历了。另外，早期人们对于回归年的周期测定有所偏差，导致他们制定的历法不够准确，以至于历法使用长了会和四季变化明显不吻合。我们也叫这些历法为阳历，毕竟它们都是基于太阳的运动制定的。我们现在得到的回归年周期（365.2422天）其实也是经过很多阳历发现偏差慢慢调整得到的，仅仅一次对于太阳的运动周期测量是很难做到准确的。而且我们还说过，回归年长度会缓慢变化，也就意味着很久以后我们的历法制定规则可能会发生变化。(www.xing528.com)

§ 3-8-7 时差

前面是在一个地点建立的时间体系，那其他地点呢？我们先考虑对于时刻的划分，然后再考虑日期。

回顾我们对于时刻的划分，我们用到的是平太阳。那么不同地点观察到的平太阳有何不同呢？假如我们让地球不动，平太阳就是在地球赤道上方以每24小时一周的速度做匀速圆周运动，那么对地球上的任何一个地点而言，当平太阳运动到它的子午面上时，这个地点就正好是12点，一天中的其他时刻也就定下来了。这就意味着，对同一条经线上的地区而言，它们的计时体系是完全一样的（因为同一条经线上的子午面是一样的）。那不同经线的地区呢？由于平太阳的运动是匀速的，且运动速度是每小时15°（可根据每24小时转动360°计算），因此，不同经度的地方每隔15°，平太阳日中的时间会相差1小时，从而所有时刻都会相差1小时。那问题是，这个差值是哪个方向变化呢？由于平太阳自东向西运动，所以偏西的经线会更晚日中，从而它的时刻会比偏东的经线小，比如0°经线12点的时候，西经15°经线为11点，东经15°经线为13点。

这样，我们就建立起了各个地点的地方时。但是我们在应用的时候会发现一个问题：只要经度有所不同，地方时就会有所不同，这很容易导致不同地区的人交流上的麻烦。比如，你可能在一个很大的城市工作，但是住在郊区。你会发现，城市和郊区的经度有些差别，从而所使用的时间有点不同，这就很不方便了。所以为了解决这个问题，不同于地方时，我们还创造了区时的概念：

我们在地球上每隔15°经度建立一个时区，在每个时区都使用其正中间的那条经线对应的地方时，这样对这个时区内的人来说，他们就可以用同一个时刻了。具体来说，以西经7.5°到东经7.5°为中时区（也称零时区），这个时区使用0°经线的地方时；然后往西分别划分出西一区、西二区、西三区……西十二区，它们分别使用西经15°、西经30°、西经45°……西经180°经线的地方时；往东分别划分出东一区、东二区、东三区……东十二区，它们分别使用东经15°、东经30°、东经45°……东经180°经线的地方时。可以看到，由于西经180°经线和东经180°经线是同一条经线，所以西十二区和东十二区其实是一个时区，我们一般叫它东西十二时区。

另外，有的国家跨过很多个时区，所以为了交流上的方便，它们可能统一使用一到两个区时的时间。比如，中国跨过东五、东六、东七、东八、东九五个时区，为了管理和交流的方便，中国统一使用北京所处的东八区时间，即北京时间。不过，这也就意味着，经度比较远离北京的区域，其日中时刻会较大地偏离12点，从而整个作息时间都偏离北京时间。比如，新疆维吾尔自治区首府乌鲁木齐经度为87°左右，北京经度为116°左右（虽然北京时间用的是东经120°的地方时），两者差了将近30°，从而地方时就差了将近两个小时。这就意味着，乌鲁木齐日出时间在北京时间早上8点左右（夏天甚至会到早上10点多），日中时间要到下午2点左右，日落时间要到晚上8点左右（夏天甚至会到晚上10点多），这就使得当地的作息时间有2小时的延迟，比如新疆的孩子们可能早上10点才上学，下午2点吃午饭，晚上7点半才放学，回到家连“新闻联播”都播完了……而一旦遇到全国统一的事情，就更加凸显出作息时间的不同了，比如全国统一高考的时候，让新疆的孩子们在早上7点半到达考场，就相当于让北京的孩子们在早上5点半到达考场，更别说该多早起床了……

好了，关于时刻的划分，我们先说到这。接下来，我们来考虑一下日期的问题。

假如在某一时刻，我们定地球上所有点的日期相同，比如为1号，那么随着地球的转动，会发生什么呢？我们会发现，在时刻为0点的那条经线偏西15°的地区，时刻（考虑地方时）为1号23点～24点；偏东15°地区，时间为1号0点～1点。过了1小时，偏西的地区全部跨过一天变成2号0点～1点，但是偏东地区仍然停留在1号1～2点。也就是说，这两块地区的日期正好差了一天。假如有人从偏西（东）的区域走向偏东（西）的区域，他会发现日期被减少（增加）了一天。

这个思想实验告诉我们，我们不可能保持地球上所有点日期总是相同，必须要有条经线将不同日期的地区分割开来。我们称这条经线为国际日期变更线。

那么国际日期变更线该放在哪里呢？最好避开有人的地区，因为谁都不希望在自己居住的地区走着走着日期就变了。我们现在将国际日期变更线放在180°经线上，这条经线大都经过海洋。而为了避开它经过的少许陆地或岛屿，我们甚至将其进行了弯折。当然了，弯折后的国际日期变更线并不影响使用。

到此为止，我们就将地球上任何一个地点的时刻、日期都建立起来了。

§ 3-8-8 二十四节气

除了根据昼夜和气候的变化建立时间体系，我们还感兴趣的一个问题是：如何给四季进行划分，比如什么时候是春天的开始，什么时候是夏天的开始，等等。之前我们在O地观测到，当太阳分别运行到H1、H2、H3、H4的时候，其气候分别是典型的春天、夏天、秋天和冬天（因此，我们其实对这4个点有特定的称呼，分别为春分点、夏至点、秋分点和冬至点，而对应的那一天也就分别被称为春分日、夏至日、秋分日和冬至日），那我们可以在它们之间取中点作为分界点。

我们测量到，春分日总是在每年的3月20～21日，夏至日在每年6月21～22日，秋分日在每年9月23～24日，冬至日在每年12月21～23日，波动幅度就一年来说很小。我们可以在这些日子间选取季节更替的日子，比如把春夏交际的日子定为是3月20～21日和6月21～22日的正中间一两天。不过我们其实可以更加准确一点：考虑到气候的变化和太阳的移动有关，且太阳在黄道上的移动不见得严格匀速，我们可以在黄道上进行等分并确定日子。

图3-20

如图3-20所示，当太阳运行到H1 H2中点时，我们就说这天是春天的结束夏天的开始，并且叫这天为立夏；当太阳运行到H2 H3中点时，我们就说这天是夏天的结束秋天的开始，并叫这天为立秋；当太阳运行到H3 H4中点时，我们就说这天是秋天的结束冬天的开始，并叫这天为立冬；当太阳运行到H4 H1中点时，我们就说这天是冬天的结束春天的开始，并叫这天为立春。

由此得到立春的日子是2月3～5日，立夏是5月5～7日，立秋是8月7～9日，立冬是11月7～8日。现在真拿到具体日子了，我们开始感觉不满意了。就拿立秋来说，立秋在每年的8月7日左右，但是这天天气仍然十分炎热，我们怎么能把它作为秋天的开始呢？想了想，我们不妨简单点，回到最初的那4天，以秋分，即9月23日作为秋天的开始。但是这样一来夏至（即6月21日）就只能作为夏天的开始了，但是这天已经很热了，作为夏天的起点又不怎么好。

问题出在，前面这8个节点之间的间距太大，温度变化幅度有些大，为此我们不妨再细分一下，在这8个点之间再进行三等分，得到24个节点，然后观察当太阳到达每个节点时对应的气候是怎样的。由此得到的24个节点对应的日子就是我们中国从古代开始就建立了的二十四节气，其对应的名字和测得的日期见表3-1。

表3-1

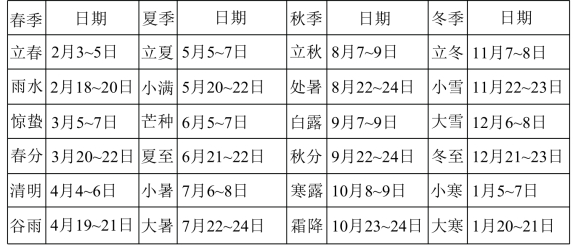
可以看到，它们的名称中都有表征气候的含义。比如，我们之前说了夏至并不是一年中最热的，而是在夏至之后的一段日子里，在这个节气表中就有反映：夏至之后就是小暑（炎热）和大暑（最炎热）。还有立秋之后的处暑（“处”表示结束），冬至之后的小寒和大寒等。另外还有反映天气现象的，比如雨水、谷雨、白露、寒露、霜降、小雪、大雪，还有反映农作物生长的，比如小满、芒种。还剩下惊蛰和清明两个节气，惊蛰的意思是冬天蛰伏土中的冬眠生物开始活动，清明就是清明节这天。^[10]

从二十四节气中可以看到，古人不单单只关注气温的变化，还关注天气现象和谷物生长等。如果只看气温变化，或许这样划分季节会更好：将小满（5月20～22日）到处暑（8月22～24日）定为夏天，将处暑（8月22～24日）到小雪（11月22～23）定为秋天，将小雪（11月22～23日）到雨水（2月18～20日）定为冬天，将雨水（2月18～20日）到小满（5月20～22日）定为春天。这会更加符合季节的交替。

不过话说回来，我开始觉得我所提出的划分季节的问题有点没必要，因为气候本身就是渐变的，我们很难将季节交替划分到天的精度，而且每年的气候、不同地区的气候都会有所不同。不过研究到这我们还是很有收获的，我们可以根据二十四节气大体把握一年的气候变化，这才是重点。

§ 3-8-9 用太阳和手表辨别方向

对于太阳还有一个非常实际的应用：用太阳辨别方向。

假如你身处野外迷路了，你知道你的营地在正南方，但是你没有指南针，也不想等到晚上再利用北极星指路，你该如何辨别方向呢？

首先，由之前的研究可以知道，只要太阳的直射纬线圈在你所处纬线圈的南方，日中的时候太阳就在正南方；只要太阳的直射纬线圈在你所处纬线圈的北方，日中的时候太阳就在正北方。一般来说，根据月份和你所处纬度很容易判断是哪种情况，当然如果你在北纬23°26′以北的地区，一年中任一天太阳日中时都在你的正南方。

有了这样一个规律，我们就可以用它来指路了。现在假设我们在北纬40°地区，那日中的太阳就都在正南方了。我们可以通过观察太阳的高度或者树影的长度确定太阳什么时候日中，从而判断正南方在哪里。除此之外，日出的太阳在粗略的东方，日落的太阳在粗略的西方，我们还可以根据月份大致判断升落方向是偏北还是偏南，从而粗略判定方向。

但是想来前面的做法也有些局限性，因为你只能在日出、日中、日落的时候确定方向，一旦太阳偏离这3个位置，你就无法使用太阳辨别方向了。而如果我们有手表，就可以在某种程度上解决这个问题。

首先从原理上要明确的是，我们是根据太阳方位变化来建立时间体系的，所以太阳的方位是和当地地方时密切相关的，这就给了我们一个机会——我们可以用当地地方时来大致推测太阳的方位。

假如我们在野外有一个指示当地地方时的手表，那么对于正午的判断，我们不必再持续观察太阳什么时候升到最高了，而只要看手表什么时候指示正午12点即可。另外，你从之前制作日晷的过程中可以看到，日晷上的6点钟刻度正好在正西方，也就意味着此时太阳正好在正东方，所以我们就知道，早上6点钟的太阳在正东方，不管它此时升得有多高（或者没升起）；同样的，下午6点钟的太阳在正西方，也不管它此时还有多高（或者落下了）。

那接下来的问题是，我们知道了早上6点种的太阳在正东方、正午12点钟的太阳在正南方、晚上6点钟的太阳在正西方，那其他时刻呢？由于太阳的影子是在日晷表盘上匀速运动的，所以如果日晷的表盘是平放在地上的，那我们非常容易判断，从6点开始，每增加1小时，太阳就往顺时针方向转过15°（以6小时转过90°计算），即：早上7、8、9、10、11点，太阳分别在东偏南15°、30°、45°、60°、75°；下午1、2、3、4、5点，太阳分别在西偏南75°、60°、45°、30°、15°。

但问题是，日晷的表盘是和地面成一个夹角的，那这种关系还能成立吗？

图3-21

首先我们要明确的是，太阳的方向是表盘上影子的反方向在地面的投影方向，以图3-21（a）为例，当OY是影子的反方向时，OY′就是指向太阳的方向。由此我们做一个极限的思考：如果表盘一直抬高到垂直于地面，那么整个表盘在地面的投影就直接是东西方向的直线，从而太阳就一直都在东西方向了！

为什么会这样呢？我们看图3-21（b）。在这张图中，假如我们先把表盘平放在地面，那么Y就在如图所示的地面位置。但是当我们将表盘绕着东西方向的直线转动着抬起来时，你会发现，在抬起的过程中，Y在地面的投影Y′会沿着正南方靠近东西方向的直线，而在这过程中，如果我们联结OY′，就会发现它在渐渐转向西方。

现在我们就知道了，如果一个地点的日晷表盘和地面夹角越大，那么我们用平放在地面的表盘给出的近似方向就和实际方向偏离越大，并且实际方向会比近似方向更加偏向东西方向的直线。那么，日晷表盘和地面的夹角与这个地点的位置有什么有关系呢？与纬度有关啊！我们之前在做日晷的时候，要求日晷表盘垂直于当地的投影球旋转轴，而旋转轴和地面的夹角就是当地的纬度，这就意味着，一个地点的纬度越小，表盘和地面的夹角就越大；一个地点的纬度越大，表盘和地面的夹角就越小。所以我们就知道了，对于高纬度地区而言，我们给出的近似方向误差不会很大，但是对于低纬度地区而言，误差可能就比较大了。

那你可能会说：“我不喜欢近似的结果，我想要精确的结果！”

这在原则上是可以做到的，但是考虑到要用到较多的数学，我们暂且不去研究。

从应用上来说，如果你觉得前面这些时刻和方向的对应关系不好记，我们还可以根据原理想出下面这个好记的方法：

我们将手表水平放置，并将时针指向太阳，那么此时时针和12点刻度线的角平分线方向就是正南方了。例如，上午10点钟的时候，你将时针指向太阳，然后寻找时针和12点钟方向的角平分线（11点钟方向），那么这个角平分线方向就是正南方了。

不过你可能会问：“时针和12点钟方向夹了两个角，我们该选择哪个角作为角平分线呢？”

我们应该选择时针和正午12点的夹角。什么意思呢？比如在早上6点钟的时候，正午12点应该在顺时针180°的地方，而午夜12点在逆时针180°的地方，因此我们应该选取的是顺时针方向的角平分线。你会发现，大多数情况下，我们选的角都是较小的那个角。

你可以对照所有的刻度进行检验，你会发现得到的结果都是和之前吻合的。而当然，你会问：“为什么这种方法是可行的呢？又为什么要选取正午12点而不是午夜12点呢？” 这个可以留着你自己思考，供解答的原理都已经在那里了。

其实大多数情况下，只要掌握了早上6点、9点，正午12点，下午3点、6点太阳的方向，其他时刻的太阳方向都可以粗略判定了，对于指路来说，精度足够了。

§ 3-8-10 房屋朝向的选择

接下来我们再展开联想举些应用的例子，比如对于飞机或者汽车座位的选择。

假如在炎热的夏季，你预定了第二天下午的一架从福州飞往大连的飞机，那么在起飞前，你该如何选择座位，使得自己不受阳光的暴晒呢？答案是：你应该选择右边的座位。因为飞机朝着北方飞行，而下午的太阳是在西方的，所以飞机左面会受到太阳的照射，从而你应该选择右边的座位。当然这个例子是最简单的例子，不过对于更复杂的例子，我们也总是可以根据飞机或汽车的运行方向以及当时太阳照射的方向进行选择。

对于座位的选择还算简单，接下来，我们运用同样的原理分析一个更复杂的问题——房屋朝向的选择。

我们都听说过坐北朝南这个词，大意就是说房屋朝向应该选择南方。不过这是解释“朝南”的，那“坐北”是什么意思呢？我们可以猜猜：如果我们把这个“坐”理解为“坐落”的意思，那“坐北”就是坐落于北面的意思。现在我们想象在一个盆地修建房屋，按照“坐北朝南”的要求，我们就应该让房屋坐落于盆地的北面，背靠山，朝南修建大门。

那为什么要坐北朝南呢？一个非常好的猜测是，朝南的采光是最好的，而“坐北”又正好可以使得阳光不受山的阻挡。我们现在就利用太阳的运动规律来研究一下，究竟朝南的采光是不是最好的。

不同纬度地区的太阳运动规律有所不同的，为了具体点，我们先考虑一个纬度，比如北纬40°的情况，然后借鉴经验再考虑其他地区。我们用之前得到的图3-9帮助我们分析房屋，或者具体点，窗户分别朝向东、西、南、北时，其采光分别是什么样的。

先考虑窗户朝向东方的情况。无论是一年中的哪个时候，太阳轨迹都是东西对称的，且总是早上偏东，下午偏西。所以在早上，尤其太阳较低的时候，太阳光可以照射进窗户。但是到了下午，太阳光就照不进窗户了。这样的话，一年中的任一天，早上采光都非常好，下午采光都非常不好了。这样也还可以，因为早上温度较低，多点阳光也好，尤其是在冬天；下午温度较高，没有阳光也没事，尤其是在夏天。

当窗户朝向西方的时候，情况就和朝向东方时相反了：一年中的任一天，早上采光都非常不好，下午采光都非常好。如此一来，早上温度较低，没有阳光不怎么好，尤其是在冬天；下午本身就热，阳光一晒就更热了，尤其是在夏天。所以我们觉得朝西的采光不如朝东的采光。

当窗户朝向南方的时候，冬天的太阳一整天都在偏南的位置，也就意味着一整天太阳光都可以照进窗户，不过只能照到窗户附近。夏天的时候，太阳整体位置偏北，只有在日中前后可以到达窗户的南面，也就意味着一天中太阳光只有在日中前后可以勉强照进窗户内的一小块地区。总结起来就是冬天采光很好，夏天采光不怎么好。这种情况就很不错了，冬天正好多点阳光暖和，夏天正好少点阳光降暑。

当窗户朝向北方的时候，冬天太阳都在南面，照不进窗户；而夏天太阳更多地在北面，从而可以照进窗户。如此一来，冬天需要阳光的时候没阳光，夏天不需要阳光的时候又有阳光，就不是很好了。

所以总结起来，我想大多数人会喜欢朝南的采光，它可以让室内冬暖夏凉，所以坐北朝南还是有一定道理的。

不过，我们在这里仅仅考虑了北纬40°地区的情形，那其他地区呢？不同纬度的太阳运动情况有所不同，我们只要改变投影球旋转轴和地面的夹角就可以了。首先，无论这个夹角怎么变，太阳轨迹仍然是东西对称，所以对于东西朝向的窗户而言，仍然只有半天可以采到光。当纬度从0°升到90°时，投影球旋转轴和地面夹角越来越大，也就意味着全年太阳轨迹都要更加偏南，所以对朝南的窗户而言，全年采光都越来越好，对于朝北的窗户而言，全年的采光都越来越差。所以综合来说，对北半球而言，可能朝南都是比较好的选择。不过对纬度很低的地区而言，四季都很炎热，这种情况下我们可能希望全年采光都少点，那么朝北会是更好的选择。当然，对南半球而言，情况就正好相反了。

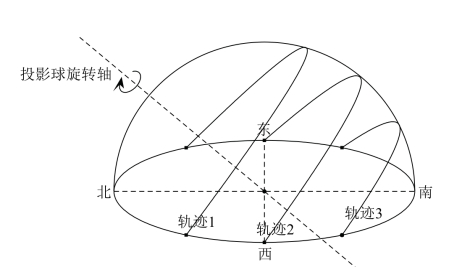
图3-9　（副本）

虽然我们比较喜欢坐南朝北，但是出于对街道以及房屋利用率提高的考虑，有时候由不得我们让每间房间都朝南。另外人们可能还不单纯考虑冬暖夏凉这个因素，有的人还就喜欢早上可以多晒太阳，或者他希望一年中阳光都可以照进房屋使其变得明媚，风大的地区的人可能还要考虑风向的影响，等等。我们可以给出不同朝向下的采光情况，但是我们不能在选择上给出绝对的结果。还有要注意到的是，我们也只考虑了东南西北四个朝向，还有东北、东南、西北、西南，等等方向没考虑。不过，方法和结果也都是类似的，我就不多说了。

§ 3-8-11 利用太阳测定经度

利用太阳的运动规律，我们还可以测量经度。我们在第二章中已经讲过测量经度的方法了，当时用的方法是，从一颗恒星升到最高点时开始计时，到达另一个地点后，等这颗恒星又升到最高点时停止计时，根据时间差来确定两个地点之间的相对经度关系。但是这个做法有一些不好的地方：一方面，我们不习惯在需要休息的晚上观测；另一方面，可能到了另外一个地点后，这颗恒星就整晚都在地平线下从而看不到，又或者它还没升到最高就日出了。而如果我们将太阳当作这颗恒星，前面的问题就都不存在了。

我们在一个地点日中时将手表设定为 12点，然后启程，到了另一个地点后，我们对比这个地点的日中时间和手表的指示时间，就可以确定相对经度关系了：假如这个地点的日中时间对应于手表上的14点，那就意味着2小时前出发地就已经日中了，同时意味着太阳从出发地子午面运动到目的地子午面的时间为2小时，那我们就知道，我们所处地点的经度相比出发地的经度偏西30°了（太阳每小时自东向西跨过15°的子午面）。接下来，我们根据出发地的经度就可以确定目的地的经度了。

不过，由于一天中太阳会在星图上略有移动，而且不是像平太阳一样正好在赤道上方匀速移动，因此，其相对地球的转动不像恒星那样匀速，从而这种测量方法的精度会比用恒星测量的精度略低点。但是由于太阳每天可见，运动又明显，而且大多数情况下我们对它的精度已经很满意了，因此，在历史上，其实这种方法被采用得更多。

§ 3-8-12 十二星座

最后，我们来讨论一下十二星座。其实说到十二星座，大家都很熟悉，有的人还比较信星座。但是十二星座是怎么来的呢？有什么用呢？又是怎么和人的性格联系上的呢？由于它和太阳有点联系，所以我们接下来就讲讲这个问题。

我们说过地球存在进动，这就意味着一段时间后地球倾向的点H2在黄道上的位置会变化，从而所有的H点都会变化，如此一来，我们之前用来描述太阳运动速度的说法，即“太阳从H1点移动到H2点所花的时间是92.7天，从H2点移动到H3点花了将近93.6天……”，可能过了一段时间后就不成立了。

当然，考虑到地球的进动非常慢，我们可以暂且不考虑这个问题。不过如果我们真的要严格展现太阳在各个位置的运行速度，我们应该根据黄道上的星图定出不同的位置来分析其不匀速性，比如太阳从星图的这个位置运动到那个位置花了多少时间……这样的描述就可以长期有效了。

那这和十二星座有什么关系呢？十二星座就可以用来表示黄道上的不同位置。3000多年前，古巴比伦人以那时候的H1点为起点，往太阳运行的方向在黄道上依次将一些比较亮的恒星通过想象力连线从而划分出12个星座：白羊座，金牛座，双子座，巨蟹座，狮子座，处女座，天秤座，天蝎座，射手座，摩羯座，水瓶座，双鱼座。它们就是著名的十二星座。如此一来，我们在描述太阳的不匀速性时，就可以说太阳从白羊座哪一点运行到巨蟹座哪一点花了多少时间，从巨蟹座哪一点运行到天蝎座哪一点花了多少时间……

另外，由于这些星座各自在天空中所占地盘不一样大，也就意味着各个星座在黄道上所占据的长度不一样长，因此，其实在2000多年前，古希腊人还引入了黄道十二宫。

如图3-22所示，当时人们以那时候的H1点为起点，沿着黄道以太阳运行的方向每隔30°划分出一个区域，这样就将黄道切成了长度相等的12个区域。这12个区域被称为黄道十二宫，并且每个宫的名字都来源于处于这个宫内的主要星座：

白羊宫，金牛宫，双子宫；

巨蟹宫，狮子宫，处女宫；

天秤宫，天蝎宫，射手宫；

摩羯宫，水瓶宫，双鱼宫。

由此我们可以知道，那时候的H1点在白羊宫的起点，即双鱼宫和白羊宫的交界点；H2点在巨蟹宫的起点，即双子宫和巨蟹宫的交界点；H3点在天秤宫的起点，即处女宫和天秤宫的交界点；H4点在摩羯宫的起点，即射手宫和摩羯宫的交界点。而现在2000多年过去了，地球绕黄轴的进动角快要有30°了，所以这4个点都往后（指逆着太阳的运动方向）退了将近一个宫了，这是可以通过目前的观测得到证实的。

你现在一定会开始猜测，可能我们现在说某个人是哪个星座，指的就是那人出生时太阳所处的星座或者宫。你查阅一下出生日期对应的星座会得到：

白羊座：3月20日—4月21日

金牛座：4月19日—5月22日

双子座：5月20日—6月22日

巨蟹座：6月21日— 7月24日

狮子座：7月22日—8月24日

处女座：8月22日—9月24日

天秤座：9月22日—10月24日

天蝎座：10月23日—11月23日

射手座：11月22日—12月23日

摩羯座：12月21日—1月21日

图3-22　黄道十二宫

水瓶座：1月20日—2月20日

双鱼座：2月18日—3月21日

从之前的二十四节气表可以看出，太阳运动到H1、 H2 、H3、 H4的日期分别为3月20日左右、6月21日左右、9月22日左右、12月21日左右，正好和前面的白羊座、巨蟹座、天秤座、摩羯座的起点日期相同。这意味着什么呢？意味着如果我们处于2000多年前，H点都未在星图上移动，这些日期就都正好和每个宫相对应，也就意味着星座的含义就是出生时太阳所处的宫。但现在的问题是，2000多年过去了，这四个H点都已经不在原先的位置了（比如，我们可能发现在3月20日这天，太阳运动到H1点了，但是现在的H1点已经不在原先的白羊宫起点，而是退到双鱼宫起点了），那也就意味着日期和宫的对应关系已经不正确了！

所以我们不得不承认的一点是，在两千多年前，人们以一个人出生时太阳所处的宫来规定这个人的星座，并且直接用日期来对应星座。但是两千多年后，在日期和星座的对应关系已经发生显著变化的情况下，我们仍然使用这样的对应规则。当然了，如果我们想要改变这个规则，使得日期和星座再度对应是完全可以的，只是问题是大家都用习惯了，不大爱去改。我们喜欢把星座和一个人的性格或人生联系起来，那是很久以前先人们留下来的传统，当时人们认为一个人出生时太阳处于哪个宫是对这个人有影响的。但是到了现在，我们对于星座和性格的联系，实际上变成了出生日期和性格的联系，已经和古人的想法完全不一样了。不过这可能还恰好使得这样的联系变得有一点点道理，因为或许出生时的气候会对人产生一定的影响，而气候正好是和日期紧密相关的。

现在，你可能会说，前面的一些应用都是无关紧要的，因为如果我们想了解太阳运行的不匀速性，我们可以在黄道上建立类似于经纬度的坐标，这会更准确；另外，十二星座和性格、人生什么的有联系可信度不高，大多数人也只是说着玩的。

那十二星座有没有存在的意义或者应用呢？其实十二星座最主要的意义就是星座本身的意义，即帮助我们描述和定位星图的特定位置。但是因为十二星座所处的位置比较特殊，所以它还有一个应用，即帮助我们寻找黄道，进而找到行星的位置。

我们之前说过，太阳、月亮、行星都是在黄道附近的，而当我们在黄道上建立了十二星座这一整条带后，它们就基本上都在十二星座上运动了。如果我们想找行星，我们只要在夜空中辨识出十二星座，或者根据十二星座中的几个画出黄道就可以大致找到行星的位置了。不过，由于晚上平均只能看到十二星座中的一半，所以我们在不同时候要有目标地寻找不同的星座。根据日期，我们可以知道太阳所处的星座，那么这个星座和其附近的星座就很难看到，同时意味着这个星座对面的那些星座比较容易看到。打个比方，6月初的时候，太阳处于金牛座，而金牛座的对面是天蝎座，因此我们就知道，当太阳从西方天空落下后，天蝎座会从东方天空渐渐升起……

对于熟悉星图的人来说，只要找到夜空中的十二星座，然后看十二星座上有没有不属于这些星座的星星，再凭借对于行星亮度和颜色的了解，就可以找到行星了（其实除了水星，其他4颗行星都比大多数恒星要亮得多，辨识度非常高）。当然了，我们也可以根据恒星眨眼而行星不眨眼的规律来找行星，但这是对于空气较好的地区而言的，对于空气较差的地区，我们发现连行星也开始略微眨眼了。空气再差点，十二星座很难辨识出来，根据星星是否眨眼来判断更是困难，这时候，我们可以根据其他较亮的星座或恒星和黄道的相对位置关系来确定黄道。当我们找到行星后，由于行星在星图上的运动并不快且本身又较亮，因此，你以后根本不用找黄道，根据附近的恒星就可以确定这些行星的位置了。

最后要说明的一点是，为了方便大家交流，我们现在已经将全天星图统一划分为88个星座，而在这样的划分下，有些规定和古人有点不一样了。比如，实际上黄道也经过蛇夫座，而古人并没有考虑这个星座，所以在天文学（相对于占星学而言）中黄道星座就有13个。另外，天文学中的处女座叫室女座，水瓶座叫宝瓶座，射手座叫人马座……当然，这些都是比较次要的人为命名和规定的问题，我们不做深入研究了。

§3-9 模型任意项

到这里，我们已经用模型推测出地球上任一点观测到的太阳方位变化，又根据这些规律引入了诸多应用，但这时候我们又要注意将模型本身和我们实实在在观测到的规律区分开来。我们观测到的规律是不存在问题的，而给出这些规律的模型却不一定唯一。和研究恒星的时候一样，我们仍然考虑模型的任意项，即在保证模型给出的规律不变的情况下，改变模型中的一些项，看这些项和原始项有什么区别，然后看有没有办法找到一些可观测的现象来确定这些项。

模型任意项1：是太阳转还是地球转

第一个任意项还是考虑到了相对性。在前面的模型中，地球不动，太阳在星图上沿着黄道运行，而黄道是包围住地球的，所以太阳其实就是绕着地球转动。现在，无论我们假设太阳绕地球转，还是地球绕太阳转，太阳和地球之间的相对位置关系都是一样的，从而无论我们使用这两种模型中的哪一种，给出的太阳方位变化都是相同的。那我们先考虑这样一个问题：假如这个世界上只有太阳和地球两个天体，那选取太阳绕地球转和地球绕太阳转究竟有无区别？

这让我们回想起之前对于地球和天球的考虑。当时我们假设这个世界上只有地球和天球，并且认为由于没有第三个物体做参考，所以选择哪个静止哪个转是毫无区别的。但是后来我们发现，不同的选择会在力学效应上呈现出不同，并且赤道地区的隆起可以用地球的自转来解释，所以我们更倾向于选择地球自转。现在回到太阳和地球谁绕谁转的问题，有没有某些力学效应是可以用其中一种选择解释，而另一种选择无法解释的呢？这次问题有点难了，我们好像想不出这样的力学效应，或许等我们以后专门研究力学的时候会想到。

当然，这仅仅是对于两个对象的思考，我们现在有三个对象了：地球、太阳、恒星。如果综合考虑这三个对象，问题就变为：选取太阳绕地球转模型，和选取地球绕太阳转模型，会对恒星模型造成怎样的影响呢？

首先，如果选取太阳绕地球转，那么对于之前的恒星模型是不会造成任何影响的，因为我们之前就是假设地球是静止的（不考虑自转）。但这是针对地球和恒星的位置关系而言的，那么太阳和恒星之间的位置关系呢？或者具体点，太阳和恒星谁近谁远？

首先我们要明确，太阳、恒星都已经远到整个地球的线度在这段距离眼里只是一个点，所以我们没办法通过测量距离得知它们的远近关系。我们得从其他角度思考。

有人会说：“我总是看到太阳遮住背后的恒星，所以我倾向于认为恒星比太阳远。”

但也有人会质疑道：“太阳那么亮，而且白天看不到恒星，你确定你看到太阳遮住恒星了？”

那人会说：“有啊，我看到日全食的时候太阳变黑了，并且只有太阳这块区域没有恒星，这不就是太阳遮住恒星吗？”

又有人会质疑道：“你知道日全食发生的原理吗？说不定是其他东西遮住了太阳，顺带把恒星也遮住了呢？”

……

看来想通过看太阳是否遮住恒星来判断二者的远近还挺难。不过我们可以从其他角度来猜一猜：如果地球不再自转，我们会看到恒星是静止的，太阳存在明显运动。而我们在生活中都有这样的感受，对于离得近的物体（比如汽车），它们的运动都很明显，对于离得远的物体（飞机），它们的运动都很缓慢，这可能就暗示着太阳比恒星要近得多。当然，我们也要意识到这样一种可能：太阳本身的运动速度很快，所以即使它离我们更远，看起来都比恒星运动快。我们现在仅仅是猜测太阳离我们比较近。

接下来，我们考虑另外一种模型，即地球绕太阳转的模型。在这种情况下，恒星的模型会发生什么变化呢？

由于太阳和地球之间的距离非常大，那么当地球在半年时间转过180°的时候，其运动范围是非常巨大的。但是对于恒星，我们并没有发现其方位有任何变化，它们看过去好像还是静止的。这只能说明两种可能：1）恒星和我们的距离已经远到了地球运动范围（包括日地距离）在它眼里都只是一个点；2）恒星在跟着地球一起绕着太阳转。后者好像不大可能，凭什么那么多恒星要跟着地球一起绕太阳转啊！那么我们就只能选择前者了。

这时候，我们就面临着一个非常有意思的结果了。如果我们选取太阳绕地球转，那我们不大好判定恒星和太阳的位置关系；但是如果我们选取地球绕太阳转，那我们可以判定恒星远到了日地距离在它眼里只是一个点。那也就是说，如果我们有朝一日能测量到太阳和恒星的距离，就可以判定是地球绕太阳转还是太阳绕地球转了。

但这好像很奇怪啊，选择不同的参考系仅仅是人主观的思考角度不同，我们怎么可能通过测量获知你在脑中选择哪种参考系呢？难道选择不同的参考系真会导致实际观测结果的不同？

其实不是这样的。之所以我们会从日心说（以太阳为中心）和地心说（以地球为中心）得到两个不同推论，是因为当我们面对从日心说得出的1）和2）两个可能结果时，我们果断抛弃了2）选择了1）。而之所以我们会做出这样的抉择，是因为在日心说下，我们的心理不大接受2），但这并不意味着2）是不可能的啊！而且，换个角度说，对于1）中的恒星远到日地距离都是个点，难道在心理上就好接受了？

其实你仔细思考会发现，不同参考系的选择仅仅是人的思考角度的不同，并不能带来实际观测的不同。那问题是，既然如此，我们为什么还要思考参考系的问题？一开始，我们仅仅是受到好奇心的驱使，但是随着思考的进行我们发现，考虑参考系问题可能帮助我们发现新问题（比如距离的问题、太阳和恒星本身运动速度的问题等），并且可以让我们从不同角度构建出不同的模型，这样我们以后或许就可以在不同情境下从这些模型中选择出最好用的模型。

现在，我们把所有模型都列出来，看哪些是我们目前比较青睐的：

模型1：太阳绕着地球转，恒星和太阳本身的运动速度差别不大，恒星和地球的距离远远大于太阳和地球的距离。

模型2：太阳绕着地球转，恒星和太阳本身的运动速度差别大，恒星和地球的距离不一定大于太阳和地球的距离。

模型3：地球绕着太阳转，恒星和地球的距离已经远到了地球运动范围在它眼里都只是一个点。

模型4：地球绕着太阳转，恒星跟着地球绕着太阳转。

这4个模型中，除了距离和运动速度的问题有实际意义，剩下的都是相对性问题，无所谓对错。从目前来说，我们还是使用地心说，毕竟用起来方便。而对于距离和运动速度问题，目前不会影响我们对于太阳的研究，我们也不打算先定下来，我们留着以后看有没有办法解决。

模型任意项2：太阳的真实运动轨迹

之前的研究仅仅是针对太阳方位变化的，而因为我们无法测量太阳在每个方位的距离，所以我们无法知道太阳在绕地球转动时的真实轨迹是什么样的。不过，有一个参数可以让我们了解太阳距离的大致变化——太阳的视直径。

我们看一个物体，如果它离得近，就会显得比较大；如果它离得远，就会显得比较小。受此启发，我们可以去测量太阳的视直径。当我们去测量的时候，我们发现太阳在一年中的视直径基本都在32′附近，没有明显的变化，只是好像冬天时会略微比在夏天时大那么1′左右，这可能意味着冬天时太阳离我们会更近点。不过这个差别太小了，所以总体来讲我们可以判断太阳离地球的距离基本不变，从而其轨迹会比较接近圆。

另外，我们再考虑太阳在这个轨迹上的运动速度。我们之前测量到太阳在星图上的移动并不是匀速的，是不是它在轨迹上的运动就一定不是匀速的呢？其实不一定。你想象一个小球以一个点为圆心做匀速圆周运动，如果你处于圆心看小球的运动，你肯定会发现小球方位的变化是匀速的，但是如果你偏离圆心看小球的运动，你会发现当小球运动到离你较近的位置时，方位变化会更快点；运动到较远的位置时，方位变化会更慢点。这其实给了我们一个灵感：会不会太阳真的是在绕着一个点做匀速旋转运动，但地球的位置稍微偏离了这个圆心，从而我们看到的太阳在星图上的运动是非匀速的呢？而这或许还有可能解释冬天太阳离我们更近点、夏天太阳离我们更远点的观测结果！我们现在就来尝试一下：

太阳从H1点移动到H2点花了将近92.7天，从H2点移动到H3点花了将近93.6天，从H3点移动到H4点花了将近89.9天，从H4点回到H1点花了将近89.0天。据此，我们可以画出图3-23来。

图3-23

你看，非常巧的是，太阳在H4点附近时（对应于冬天的时候）太阳会离我们更近点！不过这里只是画了一张草图，并不是真实比例的图形，那现在的问题就是：我们该如何安放地球的位置，使得图中的圆弧长度符合所标的天数的比例呢？

我们可以这样分两步解决：首先，我们在适当位置绘制竖直线，将圆分成左右两半，使得左圆弧长度和右圆弧长度的比例是（92.7+93.6）∶（89.0+89.9）；接着在适当位置绘制水平线将圆分成上下两半，使得上圆弧长度和下圆弧长度的比例是（92.7+89.0）∶（93.6+89.9）。画出的两条线会交于一个点，这个点就是地球所应处的位置。

通过计算或同比例绘图，我们可以得到这样的结果：如图3-24所示，地球处于圆心右偏上13.7°，而且和圆心的距离是0.033倍的圆半径。

0.033是很小的数值，地球的位置其实是很接近圆心的，以至于当圆心擦去后你根本无法通过肉眼察觉到地球不在真正的圆心。而这里，我为了表现出地球的偏心，将它画得离圆心远了点。

得到这个模型之后，我们就可以进行检验了。比如，通过这个模型，我们应该在什么时候观测到太阳运动到了黄道上的什么位置，等等。我们选几个点进行检验。我们发现实际观测结果还是挺接近模型预测的，从而它还是挺可信的。另外，因为我们还无法测量太阳的距离，所以这里的模型只有比例关系，没有准确的数值。不过，我们对太阳在黄道上位置的预测也只需要比例关系。

接下来，如果我们再考虑第一个模型任意项并让地球绕着太阳转，地球轨迹就是一个圆，而太阳在偏离圆心的位置，其定量关系完全可以由图3-24转化得到，我就不多说了。

模型任意项3：太阳究竟是什么

在模型中，无论我们假设太阳是什么，只要它能给出亮圆盘的推测结果，就都是可行的。由此，我们可以做一些假设和思考。

首先说太阳的几何构型。我们之前在恒星模型的任意项中其实已经略微考虑过了，这次我们要更加认真地考虑一下。我们观测到的太阳就是一个发光的圆盘，而仅仅由这样的观测结果出发，我们可以有无数种猜测。比如，太阳就是一个圆盘，而在太阳绕地球转的过程中，太阳总是把它的圆盘那面朝向我们；或者太阳和地球一样也是一个球体，所以不管太阳把哪一面对准我们，我们看到的都是一个圆盘状；我们还可以猜太阳是一个半球、四分之三球……

在所有的猜测中，我们首先考虑简单性：很明显，圆盘状和球状是所有构型中最简单的；然后考虑统一性：由于地球是球状的，所以如果让太阳也是球状的，那地球和太阳就都是悬浮在空中的球体了；最后考虑可能性（即巧合越少越好）：圆盘状的构型要求太阳始终将一面朝向我们，这就有点太巧了。所以，目前还是球状的构型比较受我们青睐。

然后，太阳到底是什么？

图3-24　（示意图，非真实比例）

我们看到太阳那么耀眼明亮而带有热量，其颜色又那么像火焰，我们非常容易联想到太阳是一团火球。不过这里有个问题是，这个火球的颜色和亮度会变化吗？因为我们观察到，即使是在短短的一天之中，太阳也有明显的变化：日出时呈现红色，其光线非常柔和；而后越升越高，其颜色越来越趋于金黄色，光线也越来越强烈；日中时太阳升到最高，颜色接近白色，光线最为强烈；而后太阳高度渐渐下降，颜色又渐渐趋于金黄色，光线越来越柔和；日落时，太阳又变回日出的样子，呈现红色，并且光线柔和。

这些变化是不是意味着，太阳的亮度和颜色都会在一天中发生着变化呢？但是仔细想想，我们会发现肯定不是这样的。因为在一个地点观察到日出柔和红太阳时，一定有另外一个地点同时观察到日中耀眼白太阳，但是这两个太阳一定是同一个太阳。可是，同一个太阳不可能既是柔和的红太阳又是耀眼的白太阳啊！

那么唯一的解释就是，太阳本身是不会有变化的，而是出于某种原因使得太阳处于不同高度时呈现出不同的形态。那太阳本身的形态最接近一天中的什么时候呢？由于每时每刻地球上都有一些位置是日中，而在这些位置观察到的太阳都是非常耀眼的，那也就意味无论何时，太阳本身的耀眼程度应该至少有日中时那样耀眼。那么现在的情况是：本身是很耀眼的太阳，会在其高度降低的时候变得柔和。那就有这样一种可能：当太阳高度下降时，其光线被某种东西给削弱了。

到底是什么把太阳光削弱了呢？首先，这些东西肯定在观测点和太阳之间的区域。月亮？不大可能。星星？更不可能。那么，只剩下云朵了。这个云朵好像挺靠谱，因为阴天的时候，太阳光的的确确被云朵给削弱了；甚至云朵足够密的时候，我们都敢直视太阳了。但是也有个问题是：晴天万里无云的时候，日出日落时的太阳光线仍然柔和，日中时仍然强烈，这该怎么解释呢？想来想去，我们只有考虑这最后一个可能性了——空气。

空气？这怎么可能呢？空气怎么会削弱光线呢？

我们其实可以想想大雾天的经历。雾天，我们看发光物体时，其亮度明显减低了。虽然我们不知道雾天空气中那些白蒙蒙的东西到底是什么，但是由雾的存在我们可以确定，一定存在某些飘浮在空气中可以削弱光线的东西。所以即使我们不假设空气可以削弱光线，我们也可以假设地球表面裹了一层我们不大了解的可以削弱光线的气体。我们不妨笼统地叫所有悬浮在空中的气体为大气，它包括我们平时呼吸的空气、雾天那白蒙蒙的东西、煮沸水时升起的水蒸气，还有我们不了解的气体……

我们接下来考虑这样一个假设：地球被一层厚厚的大气层裹住，并且由于重力的向心作用，整个大气层就像一个同心的厚球壳，并且它可以削弱太阳光。

有了这个假设，我们就可以解释太阳高度和其明亮程度的关系了：如图3-25所示，日出和日落的时候，太阳光穿过的大气层是最厚的，由于我们假设大气会削弱太阳光，因此自然大气层越厚对太阳光的削弱作用就越大（我们也可以将这点作为假设的一部分），那么此时的太阳光自然最柔和。而当太阳高度渐渐升高时，太阳光经过的大气层的厚度会渐渐变薄，其被削弱的程度自然越小，那么太阳光自然变得越来越强烈了。

我们还可以进一步推测：不光是太阳，其他天体也会有这样的现象。我们首先看看最易观察的月亮。我们发现月亮高度较低的时候，其亮度是较低的，但是当月亮越升越高时，亮度就越来越高了！我们再对比恒星和行星，发现情况也是如此！

图3-25

从这个假设出发，我们还发现了一个意外收获：大气对太阳光的削弱可能也是我们之前讨论过的，离太阳直射点越近，地面加热效率越高的一种原因！因为离直射点越近的地方，太阳照射下来要经过的大气层厚度越薄，那么被削弱的太阳光就越少，传输到地面的太阳光就越强烈，对于地面的加热效率就越高了。

另外，我们还欣喜地发现，如果我们再对大气层加上一个可以被照亮的假设，那么大气层还可以解释一些其他现象。比如，为什么太阳落山以后天空并未完全变暗？

如图3-26所示，图中的太阳已经降到观测点地平线以下了，也就是说，对于图中的观测点而言，太阳已经落山了，但是这时候太阳仍然可以把观测点上方的大气层照亮，从而我们在太阳落山后就仍然可以看到天空是亮的。

另外，我们还可以比以前更好地解释白天看不到星星的现象。回顾之前的解释，我们仅仅是说因为太阳光太强烈我们看不清星星，但是这样的说法很没道理。因为你可以想象：假如现在有两盏灯——一盏非常亮，亮得刺眼；另一盏则比较暗，但还能看清。你把两盏灯放一起看，你可能会因为亮灯晃到眼睛而看不到暗灯，但是如果你背对着亮灯去看暗灯，你没有理由看不到暗灯。同样的，如果我们背对太阳看星星，我们也没有理由看不到星星啊！而如果有了大气层就可以解释了：太阳把大气层照亮，因此来自大气层的亮光和星星的亮光混在了一起，大气层的亮光亮于星星的亮光，所以我们看不到星星。这就像是把之前的两盏灯放在了一起，你只能注意到其中较亮的那盏灯。由此我们甚至可以推测，如果我们可以离开大气层，我们应该可以在背对太阳的一面看到星星（或者我们只要遮住太阳不让眼睛被晃到，就可以看到所有星星了）。

不过，虽然这里的解释都非常圆满，但有的人可能在心理上无法接受——天空怎么会被照亮？其实，如果你生活在城市，你就会发现这是很常见的现象。晚上，在灯火通明的城市，你抬头看看天空，你会发现天空是隐隐发亮的；而如果你远离城市到荒郊野外，你会发现天空是漆黑一片的（不考虑星星或月亮）。天空会被地面的灯光照亮，那么太阳会把天空照得更亮就没什么值得惊讶的了。

不光如此，如果我们再假设这个大气层是流动的，我们还可能用它来解释恒星眨眼而行星不眨眼的现象。我们之前通过行星的明显移动猜测，行星离我们是比较近的，那就说明行星可能是一个亮面，而恒星只是一个亮点，只是我们肉眼无法明显区分。现在我们可以做一个小小的实验帮助我们理解为什么行星不眨眼而恒星眨眼。我们烧水的时候会有水蒸气不断冒出，如果我们透过水蒸气看一盏距离我们很远，远到看起来只是一个小点的灯，我们就会发现这盏灯在闪烁；但如果我们透过水蒸气看距离很近，近到是一个亮面的灯，我们就会发现这样的现象微弱多了。无论是行星还是恒星，它们的亮光经过大气都是会被削弱的，而我们引入大气会流动这个假设（实际上大气本来就是流动的，不然风哪里来的？）的意义就在于，让这个削弱程度随时间变化，从而让可能只是个亮点的恒星眨起眼来，而让可能是个亮面的行星保持较稳定的光源。

图3-26

可以看到，我们引入的大气层假设不但解释了太阳的亮度变化，还解释了很多其他现象。但是你可能会说：“既然大气层是太阳照亮的，那么为什么天空看过去是蓝色而不是金色的呢？无论如何我们没见过蓝色的太阳啊！还有，你忽略了颜色的问题，为什么太阳在一天之中的颜色会变化，你可以用大气层来解释吗？”

首先，对于天空是蓝色的，而太阳光不是蓝色的问题，这二者其实没有矛盾。我们将蓝色的东西放到外面去，即使此时是金黄色的太阳光照在上面，不也显示出蓝色的吗？所以大气层可能就是某种有蓝色性质的东西，从而在太阳光的照射下会呈现蓝色。那下一个问题是：为什么同一个太阳，在一天之中颜色会有所不同呢？能不能用大气层来解释呢？

我们先明确要解释的现象：太阳高度从低到高的时候，即太阳光穿过大气层厚度从厚到薄的时候，其颜色从红变金黄再渐渐变白。由此，我们可以强行引入一些假设来解释：可能太阳光是很多种颜色的光的混合光，其中包括红光、黄光、蓝光，等等，而大气层会比较容易吸收除了红光以外的其他光，所以如果经过大气层的厚度越厚，其他光就被吸收得越多，最后剩下的红光所占的比例就越多，所以我们在日出日落的时候看到的太阳偏红。为什么太阳越升越高的时候颜色从红变黄呢？我们可以解释说，太阳光中黄光占的比例较多，所以在太阳升高的过程中，黄光被吸收得越来越少以至于其剩下的量已经超过了红光，所以此时太阳光呈现出金黄色。继续升高为什么会趋于白色呢？我们可以解释说，太阳光中存在一种白光，其所占比例最大且最易被大气层吸收，所以当其被吸收得最少的时候它剩下的最多，所以日中时太阳偏白。当然，我们也可以假设所有颜色的光混合起来呈现白色，而日中时所有颜色的光都被吸收得最少……

这只是我们尝试性地针对太阳和大气层的颜色给出的一种解释，而这样的解释还没考虑到所有有关颜色的现象，所以一旦我们想拓展开来将其应用到其他有关颜色的现象时，可能就会出问题。对于光和颜色的具体研究，我们要留到光学一卷中进行。

关于大气层，还有一个问题，这个大气层有多厚呢？我们发现，利用日落到天黑的时间长度可以测量出这个大气层（起码是可以被照亮的大气层部分）的厚度：

图3-27　测量大气层厚度

如图3-27所示，（a）图是日落的情形，此时太阳的光线和我们的观测点相切，并且截出一部分大气层，这一部分大气层就是观测点上方仍被照亮的天空。过了一段时间后，天黑了，（b）图即是天黑的情形。这个时候，太阳的光线正好只能照到观测点上方的天空边缘W。通过日落和天黑的时间间隔，我们可以知道这段时间内地球自转的角度是多少，那么图中的角θ就知道了。只要这个角度一知道，我们就可以确定出大气层的厚度了：我们可以画一个半径为63.71厘米的圆代表地球，然后联结圆心和圆上一点得到一条半径，然后将这条半径绕圆心转过角θ再确定出另一条半径，这两条半径确定出圆上的两个点，我们在这两个点上画圆的切线，两条切线会交于一个点，这个点就代表着图中的W点。然后我们再量一下W点和圆上最近的一点的距离，再乘以图和实际地球的比例就得到大气层厚度了。或者我们也可以量出图中圆心和W点之间的距离，然后扣去图中的地球半径63.71厘米，最后乘以比例就是大气层的厚度了。

不过，我们仔细想想会发现一个问题：图3-27是平面图，而实际上地球和太阳光都是三维的，因此上面这个分析只适用于在赤道的观测点，而且还要求当天太阳是在正东升起正西落下。不过其实仔细想想，你会发现上面的图还适用于另一种情况：在春分日或秋分日的时候，太阳光是和任何一个地点的纬线圈重合的，那也就是说，如果我们从南极或者北极朝着这个纬线圈看，我们看到的图像就会是图3-27的样子，只不过这时候图中的圆不代表整个地球，而是代表纬线圈。如此一来，我们就不必移动到赤道，只要等到春分日或秋分日的时候进行测量就可以了。并且我们还可以由图判断，因为大气层厚度在各个地点都相同，所以如果当地的纬线圈越小（纬度越高），那么当地测量到的角θ就越大（从日落到天黑的时间越长）。

现在我们可以去测量了，比如我们就在北纬40°地区测量，并且为了避免地平线上树木的遮挡，我们可以在海面上观察海上日落来测量。但是在测量的时候，我们又发现两个问题。第一个问题是：日落时，是太阳刚碰到海平线时开始计时，还是落到一半时，或者完全落下时开始计时呢？另一个问题是：如何确定天真的黑了呢？凭感觉吗？

对于第一个问题，我倾向于认为是在太阳完全落下时开始计时，因为天完全黑的时候，是太阳顶部（而不是中心或底部）正好无法照到测量地上方天空的时候，所以我们也应该在太阳顶部完全落下时开始计时。

对于第二个问题，除了凭感觉，我们还可以想出一个比较准确的方案：首先，我们得避开城市到一个没有地面光线干扰的地方，然后朝着日落的方向看。当看到这个方向最暗的一颗星都显露出来的时候，我们就认为天已经完全黑了。这么做的原理在于：我们刚刚说过，之所以我们白天看不到星星，是因为太阳光把大气层照亮了，那么当太阳光对大气层毫无影响的时候，星星（包括最暗的星）就可以全部显露出来了。那么怎么确定哪颗星最暗呢？我们可以在前一天（要保证这两天天气情况相同）午夜观察星空，找那些几乎快看不清的星星。

通过这个方法，我们在北纬40°的春分或秋分日测量到，日落到天黑所维持的时间将近为1小时22分钟，从而可以得到角θ为20.5°左右，再根据北纬40°地区的纬线圈半径4880千米（这也可以通过作图或计算获得），可以得到大气层的厚度为80千米左右。现在我们就知道了，起码在我们天空上方80千米左右的地方，不存在可以被照亮的气体，又或者说即使它们被照亮了我们在地面也感受不到了。

可以看到，大气层的引入解释了相当多的现象，我们还测量了大气层的厚度，大气层的存在就变得十分可信了。现在回到有关太阳的研究中，我们就可以大胆地说，太阳在不同形态间的变化是因为大气层的影响，而非太阳本身的变化了。

不过，说到这里，我们又想到了一个问题：日食现象该怎么解释呢？

日食不是经常见的，但是这个现象太难以置信了：每天高悬空中的明亮太阳突然部分或整个丧失了光芒。难道说我们之前假设的一团火球偶尔会熄个火？不大可能吧，因为即使它要熄火，干吗有时候全部熄火有时候熄一部分，而且那么大个火球要是熄火了该怎么重新点燃啊，毕竟日食持续的时间不长……

如果我们不想假设太阳在日食期间熄火，那我们只能假设是某个东西遮住太阳了。那有哪些东西可能遮住太阳呢？大气层？不大可能，按照我们之前的假设，太阳光是可以通过大气层的。星星？也不大可能，星星太小。唯一剩下的就是月亮了。如果我们在日食前后一段时间注意一下月亮，我们就会发现这段时间的月亮的确非常靠近太阳，并且月亮是一个非常弯曲的亮钩，亮的边缘正好指向太阳。月亮亮的部分指向太阳提醒我们，月亮本身不是亮的，而可能是太阳把月亮照亮。并且我们可以猜测，当月亮移动到我们和太阳之间的时候，月亮会遮住太阳，这样不就日食现象嘛！我们肯定还想继续研究一下月亮和日食现象，不过不急，我们等到研究月亮的时候专心进行，我们只要知道可以在不假设太阳会熄火的情况下解释日食就好了。

接下来是涉及测量精度的任意项，比如太阳转动周期会不会缓慢变化，黄轴会不会缓慢变化方位，等等。不过，因为我们之前本就考虑过长期的观测，所以这些任意项只能对于更加长期的观测了，我们就不管那么久远的事情了。当然，我们之前猜测过回归年的周期是会缓慢变化的，希望有机会可以检验。关于太阳的模型多样性，我们就先考虑这么多了，留下的一些问题我们之后再解决。

§3-10 下一步研究对象的拟定

对于太阳的研究告一段落了，我们接下来要选取下一个研究对象。我们之前说过，在地球上观看行星的时候，各个地点看到的行星方位都是平行的，从而对地球上不同点而言行星方位的预测较为简单；而观看月亮的时候，在不同地点观察到的月亮方位并不平行，从而对不同点的月亮方位预测更困难。但是，初步研究告诉我们，行星的运动太慢了，我们要花费很长时间来研究，而月亮的运动就快得多。另外，我们还觉得月亮更显眼、更重要点，所以综合来说，我们下一步的研究目标选取月亮。

§3-11 补充内容：云

在这章的结尾，我同样要加入一些补充内容，不过这次的补充内容只有一项——云。

我们曾在仰望天空时说过，我们研究的对象会是日月星辰云朵，但我们很快就意识到日月星辰和云朵是两类非常不一样的对象，从而渐渐把注意力放在了前者而忘记了后者。不过，现在我们要研究一下云。

云本身的形态以及方位变化相当多变且不规律，我们要研究的就是规律，如果没有规律也就没什么好研究的了。当然，这仅仅是根据日常生活经验得到的武断的判断，而更加严谨的做法应该是做一些具体的记录，比如，我们可以每天记录天上云的数量、形状、运动速度和方向等，然后看随着天数的变化有没有特定的规律。最终我们得到的结果是——基本上没有什么规律。

虽然说云在其本身形态以及方位变化上没什么明显规律，不过我们还可以研究其他问题，比如云和地面的距离。首先，云可以遮蔽日月星辰，说明它肯定比日月星辰要近，这样，我们或许可以通过在地面拉基线测量到它的距离。果然，我们发现云其实和地面非常近，总体来说只有几千米，不过不是定值，有的稍高有的稍低。

这样的近距离给了我们启发，如果我们生活在海拔比较高的地区，就有可能直接触碰到云。为此，我们可以仔细观察一些高山，我们会发现在合适的时候可以看到一些高山穿过云层，这样我们就可以爬上这座山来近距离观察一下云到底是个什么东西。

当我们在山脚看到山顶被云遮住的时候，我们往上爬。随着我们越爬越高，我们发现周围的能见度在不知不觉中渐渐减低，有时候我们会看到像空调放出来的冰凉水汽在空中飘动——我们已经处于山顶的云之中了！而在云中的感受就像是雾天在地面的感受，有些不同的是，山顶的云湿度很大，我们摸一把悬浮的水汽会发现自己的手变湿了，这其实暗示着雨是从云来的。所以某种程度上，我们可以把云理解为是海拔较高的雾，只不过这些雾主要是由悬浮水汽构成的。而至于云为什么会移动，我们在山顶很快就会知道那是因为被风吹动的缘故。这样，我们就可以把云纳入大气层的范畴了。

【注释】

[1]这个计算过程比较复杂，你只要知道在一切都确定的情况下，它总是可以通过做比例模型得出就可以了。后面也有一些或简单或复杂的计算过程被我省略了，我就不再强调了。

[2]“气温相反”这个说法好像有点问题，不过我想你知道我的意思。

[3]图中的圆盘显得一半处于地下，这是为了让你看清东西南北。圆盘肯定是处于地上的。

[4]在这里，我是为了让问题简单才用“太阳绕着针转”这样的说法，如果你想深入理解，你应该想象一束平行光绕着针转动，而且这束平行光会随着太阳直射点的变化而改变照射的方向，从而针影的长度会发生变化。理解了这个，你会发现当直射点到了南半球的时候（假设我们在北半球），平行光会从圆盘底部往上照，从而针无法在圆盘上留下影子。但这个问题很好解决，我们让针从底部穿过圆盘，并且在圆盘背面也刻上刻度，这样日晷就是两面用的了。

[5]图中只等分到小时，如果你想更精确，你还可以在每个小时内进行等分。

[6]因为我们把原子钟作为计时标准和授时仪器，所以这里的“匀速”其实是我们规定的。

[7]这也是为什么我们选择引入闰秒而不是改变钟表运行速度的原因。

[8]当然，我们没学过原子物理就不知道这是什么意思，但你只要知道这是为了符合原始时间长度设定的新定义就好了。

[9]之后你在“月亮”一章中会看到，还有一种指示月亮阴晴圆缺的历法叫阴历，并且阴历的一个月也是三十天左右，和这里讲解的公历很接近。但不同的是，阴历对每个月天数的设定是根据月亮获得的，而公历和月亮完全没有关系。可想而知，要么公历是从阴历发展来的，要么公历对月份的设定模仿了阴历的设定。

[10]这些节气的名称具体什么意思，你可以自己去查询，我并没有全部说清楚。