实验回顾：力的合成和分解

1.教材要求

牛顿在著名的《自然哲学的数学原理》中曾把共点力的合成和分解作为三大运动定律的推论。

高中物理教材在力的初步概念基础上，通过实验分析，归纳出力的平行四边形法则，明确提出力是一个矢量，并指出平行四边形法是矢量合成、分解的普遍法则。在具体的教学中，下述几点必定是教材的关注点。

（1）矢量是学生第一次接触的概念，教材以力这一物理量的特征作为典型，提出矢量。矢量概念的建立有一定的难度，学生习惯于单纯从量值大小认识物理量，教材中要突出力的大小和方向是共存的。

（2）矢量和标量在运算法则上有根本的区别，标量的合成是代数的加法，矢量的合成是平行四边形法则。学生掌握平行四边形法则是正确理解矢量概念的核心。平行四边形法则也是研究物体平衡条件以及深入学习的基础。

（3）力的合成和分解都体现了等效方法的运用，合力和它的分力是一种等效力，这种等效替代的概念虽比较抽象但学生又会感到新鲜和奇妙。这些问题如果仅限于直观体验的描述，远谈不上对概念本质的揭示和把握，而应用实验手段定能成为处理这些问题的利器。

2.实验手段

图3—7—1为力的合成和分解实验的传统实验工具。图3—7—2所示为使用上述传统实验工具验证（或探究）两个共点力的合力大小与分力的关系的实验，目的是为了对力的平行四边形法则有所认知。

图3—7—1　力的合成和分解实验的传统实验工具

图3—7—2　用传统实验工具验证平行四边形法则

用图钉把橡皮筋的一端固定在A点，橡皮筋的另一端拴上两个细的绳套，用两个弹簧测力计互成角度地拉橡皮筋，使橡皮筋伸长到某一位置O；从O点沿着两条绳套的方向画直线，按选定的标度作出这两只弹簧测力计的拉力F1和F2的图示，以F1和F2为邻边作平行四边形；过O点画平行四边形的对角线，作出合力F的图示（图3—7—3）。

图3—7—3　两只弹簧测力计的拉力F1和F2的图示

从模拟方法到数字方法，从间接到直接：

研发中心成立以来的工作经验告诉我们，DIS实验与传统实验的区别，就是让测量从模拟方法过渡到数字方法，让学生对实验现象的认识，从间接方式转为直接方式。围绕着力的分解与合成实验，DIS几代实验器的开发就证明了这一点。

只用一只弹簧测力计通过细绳套把橡皮筋的结点拉到同样的位置O，记下弹簧测力计的示数和细绳的方向，同样作出这只弹簧测力计的拉力F′的图示（图3—7—4）。(www.xing528.com)

图3—7—4　弹簧测力计的拉力F′的图示

如果力F′与用平行四边形法则求出的合力F在大小和方向相同，就可以说明它们之间是等效的。

实验虽然简单，但学生对力的平行四边形法则的领悟和对等效替代这种科学方法有了直接体验，实际上已经触及这些概念的内涵。全国有多套教材采用此内容作为“力的平行四边形法则”的验证性（或探究性）学生实验。

3.相对成熟的实验装置

图3—7—5所示为“力的合成与分解演示器（J2125）”。该演示器一改学生实验在水平面上操作为竖直面上进行演示。在一个分度直角坐标盘上，借助细绳汇集合力和分力于一个圆环上，使圆环的中心能在坐标原点的位置。分力由若干定值钩码给出，坐标的分度指示出挂线的夹角大小，合力则从连接圆环的弹簧测力计测出。实验时按照给定的两个分力F1、F2的角度大小，调整滑轮的位置和加挂钩码的个数，调整弹簧测力计的上下位置和角度，使圆环在两个分力和弹簧测力计的共同作用下处于悬空状态，且与坐标盘圆心重合。此时弹簧测力计显示的就是两个分力的合力，当分力是对称时，即分力的大小相同并分居坐标盘垂直两侧的角度相同，合力的方向必与垂轴重合，弹簧测力计保持在垂轴上。

在不对称的分力作用下，合力必偏离垂轴的一个角度，需调节弹簧测力计偏离垂轴一个角度，使圆环坐标同心（图3—7—6）。

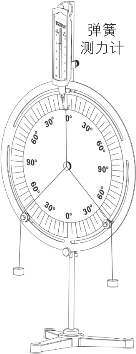
图3—7—5　力的合成与分解演示器

图3—7—6　圆环坐标同心

力的分解是力的合成的逆运算，并同样遵循平行四边形法则，用此实验器也可演示力的分解。

该实验器还可用作共点力的演示实验，实验证明：在共点力作用下，物体的平衡条件是合力等于零。

4.传统实验手段综述

以上传统实验手段的优点是简单、直观。缺点则是手工操作步骤繁多，对技巧要求较高，实验时读数、描点、画线等步骤费时费力，且学生上手后实验误差普遍较大。

采用上述手段进行力的合成和分解实验，只能进行静态测量，无法进行动态研究，尤其是两力夹角的测量与计算，更是实验操作过程中的难点。而如果不能够在动态变化中展现力的大小及方向的实时变化，学生对于“矢量”的认识，还是处于不完整的状态。为此，笔者曾经在三十年前开发了一套教学模型（图3—7—7），来演示合力随两个分力的夹角改变而改变的现象。尽管当时也取得了不错的教学效果，但现在看来还是偏重于定性观察，定量测量的效果还不是很理想。

图3—7—7　自制教学模型