实例研究：数学课程对学生成绩的影响

该实例来源于赖尔登（J.E.Riordan）和诺伊斯（P.E.Noyce）的研究成果，它利用配对比较方法，调查分析两个基于标准的数学课程对学生学业成绩的影响.［15］

这项研究成果清晰描述了研究的现实背景，对已有研究进行系统综述.在这基础上，系统介绍研究使用的工具和方法，对数据的统计和分析，然后得出基于证据的结论.最后在对自己研究分析的基础上，提出这一课题研究的局限性和建议可进一步研究的话题.

6.2.2.1　研究背景的分析

课题组在分析研究背景时首先指出，1989年美国数学教师协会（National Council of Teachers of Mathematics，简称NCTM）发布第一个国家性课程标准《学校数学课程与评价标准》，针对现代信息社会教育的各种需求，提出数学教育目标应当是培养有数学素养的社会公民，并对“有数学素养”提出5项条件：懂得数学的价值；对自己的数学能力有信心；有解决数学问题的能力；学会数学交流；学会数学推理.［16］

此后，在1991年和1995年，NTCM又先后编制发行了《数学教学的职业标准》（1991）和《学校数学的评定标准》（1995）.前者旨在为数学教师的日常工作提出指导性意见；而后者则阐述了进行数学教学评定的方法，为教师提供评定数学教学质量的标准.虽然这些标准只是作为指导性文件提出，并不具有法律效力，但美国的许多州教育机构在设计本州的课程计划和测试方法时都将其作为主要的参考依据.

赖尔登和诺伊斯主持的课题组以美国马萨诸塞州为例，分析当时州层面的课程改革计划.1993年马萨诸塞州立法机构通过了全面开展教育改革的法案，要求建立州一级的课程框架以及基于州立标准的新评价体系.经过两年的讨论修改，1995年美国教育委员会（Board of Education）通过了马萨诸塞州数学课程框架“获得数学力”，该框架随之在全州推广.它主要参考NCTM的《学校数学课程与评价标准》（1989），更为强调学生的推理和概念性理解.1998年开始实行新的评价体系，即马萨诸塞州综合评价体系（the Massachusetts Comprehensive Assessment System，简称MCAS），该评价体系面向4年级、8年级和10年级的所有学生，它是一种标准参照的测试，主要依据课程框架及与之配套的评价指南.这一综合评价体系中的数学评价部分覆盖四个内容领域：数感；图形、关系和函数；几何与测量；统计与概率.每个领域的测试题型包括开放题、简答题和选择题.

课题组还分析了自1989年以来一些研究组织和团队着力开发的基于标准的数学课程项目.他们指出，自美国公布首个国家性标准以来，不少的开发团队为教师提供丰富的课程资源，鼓励教师在数学教学中尽量体现国家性标准的思想.例如，芝加哥大学学校数学项目组开发了“每日数学”（Everyday Mathematics，简称EM），它面向学前班至6年级.这一课程项目旨在让学生以小组学习活动为主，利用可操作性工具、计算器和其他数学工具探索数学概念，鼓励学生探究并且分享解决问题的多元方法.该课程项目教授的数学主题包括数据，概率，几何和空间感，测量和测量方法.又如，受美国国家科学基金（National Science Foundation，简称NSF）资助，由密歇根州立大学开发的数学课程项目“连接数学”（Connected Mathematics，简称CM），它是为6～8年级学生开发的问题中心的课程.该课程将数学课程分为三部分：提出（引发）问题、探索问题、总结问题，从而帮助学生实践他们所学的内容.它让学生通过各种方式演示自己所学的内容，包括小组问答、项目活动、单元测验以及自我评价等.该课程项目还建议学生编制学习日志和使用图形计算器等.

但改革过程总是充满各种不同的声音，尤其是那些数学课程改革项目受到了某些研究者或研究团队的质疑.美国教育部为此组织专家委员会，对各个基于标准的数学课程改革项目进行评估.专家委员会要求那些项目开发组递交基于研究和基于证据的项目分析报告，他们再根据递交的研究报告，将那些课程项目认定为示范性项目或前瞻性项目.［17］示范性和前瞻性项目的差异在于，如果开发组提供了令人信服的、能体现参与课程项目的各个学校的成功的证据，那么该课程项目被认定为具有示范性的；如果开发组只提供证明课程项目成效的初步证据，那么该课程项目被认定有前瞻性.其间，专家委员会将EM项目列入前瞻性系列，将CM项目列入示范性项目系列.

6.2.2.2　问题提出

该课题组在分析研究背景时指出，递交给专家委员会的课程项目评估研究报告，并没有对参与项目的学生的学业成绩进行测评，或者在研究选样上存在缺陷，往往只挑选乐于实施改革项目的一些学校作为分析样本.针对这一现实背景以及课程评价研究的不完整性，该课题组试图对在马萨诸塞州实施的两个基于标准的课程项目“每日数学”（EM）和“连接数学”（CM）进行系统的调查分析，提出如下研究问题，即这两个课程项目对学生数学学业成绩带来怎样的影响.他们的研究假设是：在实施特定的基于标准的课程项目的学校，其学生在马萨诸塞州的标准化测试中获得的成绩，要比那些对照组学校的学生成绩高，并且在课程实施过程中，那些参与课程项目的学校学生的学业成绩进步更快.

6.2.2.3　研究综述

课题组在明确了研究背景及其意义后，对相关的文献进行综述分析，总结出若干课程评价研究的特点，即大部分对于基于标准的数学课程项目的评价研究是由课程开发者自行组织与指导的，这些研究提供了初步的关于学生学业成就发展趋势的数据.例如，课题组分析了卡罗尔（W.M.Carroll）的评价研究，该评价研究报告了在芝加哥地区使用“每日数学”课程的学生参与伊利诺伊州标准化测试后的成绩，并且与某个郊区没有使用该课程的学生成绩作比较，或者将某个使用“每日数学”课程的学区与相似的、没有使用“每日数学”课程的学区作比较，相似的指标包括学校规模、学生人均经费、学生人口统计数据.［18］课题组也分析了本-哈伊姆（D.Ben-Chaim）等人关于使用“连接数学”课程对学生学业的积极影响的研究，尤其在解决比例推理的各种任务时，与没有使用“连接数学”课程的学生相比，成绩提高很多.［19］

课题组还综述了其他类型的相关研究成果.例如，有些研究报告了基于标准的课程项目成功的共同特征以及实践表现.有些研究，将学生的学业成绩与学校为了适应基于标准的课程所实施的教学实践结合起来.如定量的理解：放大学生的成就与推理（Quantitative Understanding：Amplifying Student Achievement and Reasoning，简称QUASAR）研究项目，对经济不发达地区的中学数学课程改革进行研究，提供的研究证据说明，课堂教学中使用的数学任务的性质将影响学生数学学习结果.特别是研究者斯坦（M.K.Stein）和格罗弗（B.W.Grover）等发现，“数学任务的构造是一个很有价值的研究焦点，它有助于凸显数学内容和数学过程”.［20］QUASAR项目开发了系列测试任务，包括结果开放的试题，用于测试学生问题解决、推理以及数学交流能力；也包括关于数与运算、估算、图形、代数、几何、测量、概率和统计方法的测试任务.

6.2.2.4　研究方法

课题组在全面把握已有研究成果的同时，设计将在研究过程中使用的各种研究方法，包括数据收集、实验组学校的确定、对照组的选择、教师特征分析等.

数据收集

课题组使用的最原始数据来源于1992年和1996年马萨诸塞州教育评价项目（the Massachusetts Education Assessment Project，简称MEAP）的测试结果和1999年马萨诸塞州综合评价体系（MCAS）的测试结果.

另外，从马萨诸塞州教育部管理的数据库的“1999年公立学校报告”中，收集了学校层面的学生入学信息，包括减免午餐费用的资格信息和种族信息.还从马萨诸塞州教育管理的“数学、科学和技术调研”数据库中，收集了关于该州课程使用的信息.他们和当地教育管理人员核实当地学校所使用的数学和科学课程，了解是否调研、预实验或者实施着课程.

1999年马萨诸塞州综合评价中关于教师的问卷调查信息也被用于这个课题的教师以及教学分析中.

实验对象组的确定

这次调查分析不是抽样调查，而是覆盖到所有参与改革型课程的学校.因此课题组首先确定所有在马萨诸塞州使用“每日数学”（EM）或者“连接数学”（CM）课程的学校.数据来源是州教育部组织的1999年“数学、科学和技术调研”，以及出版机构提供的购置“每日数学”课程或者“连接数学”课程的信息.

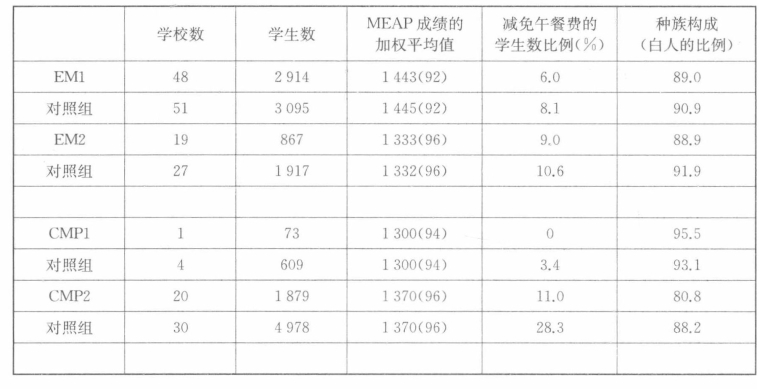
由于“连接数学”课程项目以单元模块组织的，因此课题组在研究中只选用了1998年和1999年期间从6年级到8年级，至少使用了11个单元模块的学校，共有21所学校.但其中1所学校使用“连接数学”已经四年，将它归入CMP1，其他20所学校使用“连接数学”课程2～3年，将它们归入CMP2.另外有67所学校使用“每日数学”课程，其中48所学校已经使用“每日数学”四年以上，这些学校被归类为EM1.其余19所学校使用“每日数学”课程2～3年，就将它们归入EM2.因此该课题确定的实验组分为四类：CMP1，CMP2，EM1，EM2.

在确定实验组的时候，这个课题组还收集学校原来在州标准化测试中的成绩（MEAP），减免午餐费的学生比例、种族特征等，为选择对照组所用.

对照组的选择(www.xing528.com)

针对上面确定的四类实验组学校，要选择没有实施“每日数学”或者“连接数学”课程的对照组学校.

首先根据先前的州标准测试成绩进行配对，然后根据每个学校减免午餐费的学生比例配对，最后再考虑学校学生的种族构成.最终关于实验组和对照组的数据信息如下表6-2所示.

表6-2　实验组和对照组信息对比

课题组分析了对照组学校使用课程教材的情况.具体数据信息来源于州教育部管理的“1999年数学、科学和技术调研”.其中小学层面，78所对照组学校使用15种不同的教材；在中学层面，34所对照组学校共使用15种不同的教材.

教师特征分析与教学实践

在完成学校配对后，课题组分析了实验组和对照组学校的教师特征的自查报告，整理其教学实践的信息.他们的假设是要质疑这样一种观点，即学生的成绩与教师专业资格能力的关系比与课程影响的关系更为密切.因此，课题组借助1998年MCAS向所有4、8和10年级学校校长以及教师做的问卷调查，对实验组和对照组学校教师进行比较.

教师特征问卷涉及如下一些信息：近两年获得专业发展机会的小时数，教龄，证书类型，所完成的大学数学课程门数，是否为某专业协会中的成员，参与数学会议的频率.

教师教学实践的问卷：摘自美国RAND（Research and Development）研究，主要调查改革和传统的教学实践对中小学生数学和科学成绩的影响.

6.2.2.5　研究结论及其分析

课题组运用配对比较的后处理研究方法，旨在检验课程对学生学业成绩的影响.研究结论从学生层面和学校层面进行报告.

学生层面主要是检验在1999年测试中实验组和对照组学校学生的分数，然后按照种族、性别和减免午餐费分别进行比较.学校层面，比较实验组和对照组在一个时间段上成绩的变化.

学生层面的比较

课题组经过精心、科学地收集和处理数据后，得出相关的研究结论.例如，课题组得出，马萨诸塞州4年级学生在使用“每日数学”课程后，其成绩远远高于只用传统课程的对照组的学生成绩；马萨诸塞州8年级学生在使用“连接数学”课程后，其成绩也远远高于只使用传统课程的对照组的学生成绩.基于标准的课程对学生学业成绩有积极影响，且这种影响不会随学生的性别、种族和经济条件差异而不同.班级中成绩优秀、成绩中等以及成绩较差的学生，通过基于标准的数学课程的学习，都有不同程度的提高.另外，还得到额外的结论，实验组学生在四个数学内容领域上的成绩都高于对照组，在三种不同类型测试任务上也高于对照组.对那些至少实施四年课程改革内容的学校，学生在学习上的收益保持稳定或者不断增长.这些收益不能归因于教师专业资格的差异，也不能归因于教学实践自我报告的差异.

学校层面的比较

课题组确定的使用“每日数学”的实验组包括：一组是较早使用“每日数学”课程，这组学校在最初实施改革课程的两年，成绩收益较低（0.19），而到了1996年至1999年，成绩收益得到完善（0.37）.而较晚开展“每日数学”课程实验的学校，在2～3年内的成绩收益为（0.31）.这些结论说明，随着使用“每日数学”课程的深入，对学生成绩的影响是正面且积极的，这些结论与其他研究项目得出的结论相吻合.

而较早使用“连接数学”的（只有一所学校）8年级学生有类似的收益，1996年到1999年学生学业成绩保持稳定.

在不同类型测试问题和不同测试内容上的比较

课题组利用1999年综合性评价（MCAS）的数学学业成绩，分析学生面对不同类型试题和不同测试内容上的分数.数据表明，参与“每日数学”课程的学校在各类试题以及测试内容上皆获得比对照组更好的成绩，参与“连接数学”课程学校的学生学业成绩也远远高于对照组学生.

课题组对数据的精心分析，论证了他们提出的研究假设，即参与“每日数学”或者“连接数学”课程项目的学校成绩高于对照组，它们对学生学业产生积极响应.

6.2.2.6　局限性以及对未来研究的建议

课题组也指出课题研究有一定的局限性，表现为实验组和对照组学校都是较好的学校，也就是说，这些学校要求减免午餐费的学生比例较低，且大部分是白人.然而，这项研究也对不同学生群体进行分析，非白人以及低收入者的学生，实验组的成绩同样高于对照组的成绩.课题组认为，今后有必要去研究低收入家庭和少数民族学生的学业成绩与课程实施的关系.

该课题没有关于教师实践的详细信息，也没有做课堂观察，关于教师实践的信息来源于州级层面对教师的问卷调查.这些信息反映出实验组和对照组教师的实践差异很小，但这些信息是自己报告的.对此，课题组提出了今后进一步研究的问题，如，可以检验个体学生在数学学业成绩上的发展，检验这些课程对特殊学生群体的影响.这一课题结论充实了关于基于标准的课程对学生学业成绩有积极影响的证据.