美国中学数学课程问题解决

20世纪70年代至80年代，问题解决成为美国数学教育研究的一个重点，问题解决的兴起源自美国对课程“回到基础”的反思.1980年，NCTM公布了一份名为《行动纲领》（An Agenda for Action-Recommendation for Mathematics of the 1980's）的文件，该文件提出了八项建议，强调在数学教育过程中开展“问题解决”教学.行动纲领第一条明确提出：问题解决是20世纪80年代学校数学教育的中心.数学课程围绕问题解决组织，问题解决的定义、语言应被发展扩充至数学表征的策略、过程、表达模式等，数学教师应创设促进问题解决的学习环境，各地方应组织有利于促进所有年级数学问题解决能力的课程资源，数学课程应组织所有学生通过数学应用参与到问题解决中，研究人员及资助部门应优先考虑调查研究问题解决的本质、有效促进问题解决的方式.

至此之后“问题解决”逐渐成为各国中小学数学课程改革和研究的核心，它推动了课程改革或者说基于标准的课程改革.90年代中期后，人们对问题解决的关注逐渐转移到其他领域，但即便如此，这些领域的研究也常涉及问题解决.莱斯特（F.K.Lester）在1994年总结了从1970年至1994年有关问题解决的研究，研究重点与主要方法见下表：［46］

表5-3　1970年至1994年问题解决研究归纳表

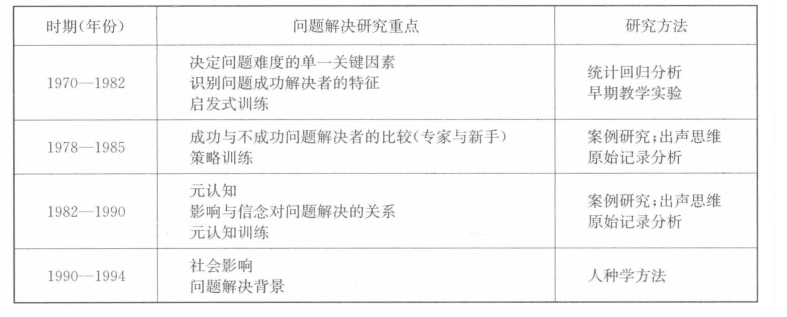
从1970年至1994年，问题解决的研究有了重大发展，但是仍有许多问题没有解决.在应用方面，需要进行直接实验，研究能使学生学会使用大量问题解决策略的练习的程度和类型.在理论方面，仍有基础性问题有待解决，研究仍未解释人们选择问题解决策略的方法与原因，即现在的研究框架提出了问题解决的特点，但是没有提出问题解决的理论.20世纪80年代，问题解决研究有所减少，但是并不意味着研究没有进展，只是表现在不同的方面.在这个时期，问题解决研究有实际方面的影响，NCTM于1989年发布的《学校数学课程与评价标准》，明确指出问题解决、推理、数学练习、用数学计算是数学教学的重要目标.为实现这些目标，研究者们开始设计教学，并常使用“设计实验”探索其背后的理论.设计实验起初是面向内容与方法的，通过新的教学手段促进概念理解.早期的问题解决研究主要发生在实验研究中，随着课程改革与标准的实施，学习环境的研究兴起，研究逐渐将数学作为一种有意义的活动，并提出了发展新的分析技术和视角的需要.

20世纪90年代开始至今，研究者开始使用一系列工具、技术手段、观点等来描述学习环境，其中有关问题解决研究结论主要如下：

（1）数学是一种意义建构.

研究表明传统教学（主要为技能导向）相比基于课程标准的教学存在异同.学生在两种课程教学下在有关技能的测试中表现相同，基于课程改革教学下学生在概念理解、应用、问题解决方面的表现明显优于传统教学.

（2）对话共同体.

通过对多样课堂环境研究，探究课堂机制，主要包括课程的价值、实际功能.其研究包括课堂对话模型的检验，学生进行有意义决策方式的研究.课堂实践的检验，包括社会性教学标准概念、问责结构的研究.社会性教学标准是指描述数学课堂中作为共享的教学行为的模式特点，如对数学情境包含的内容作出一个详细的解释.

（3）问责结构.(www.xing528.com)

问责结构用于规范学生数学学习的严谨性.

（4）丰富的课堂文化.

恩格尔（R.A.Engle）和科南特（F.C.Conant）认为高效且丰富的学习环境有共同的特征：

问题化：学生投入于智力问题；

决策性：学生被授予解决问题的权利；

责任性：学生的智力活动符合他人及学科标准；

资源：学生被赋予充足的资源从事上述活动.

在问题解决的应用方面，通过教学帮助学生掌握多种问题解决的策略，这些通过基于标准的课程实现.理论上，如将波利亚所描述的启发式问题解决策略水平进行分解，即将复杂的启发式策略分解为相对简单、可学的策略.其中元认知，尤其是自我监控的作用不仅存在于数学问题解决过程中，它存在于所有学科的问题解决过程中.

在理论方面，从20世纪80年代开始，研究已从实验室转移到课堂，一些研究工具与技术有助于形成有意义的学习环境.其中数学问题解决可被视作一种目标导向的活动，最主要的目标是解决问题，通常伴随着一些子目标和替代目标.在实现各子目标过程中，当子目标不能实现时，由其他目标替代，并接受其他知识，最终状态是问题解决或个人放弃.

事实上，美国与课程相关的问题解决如同钟摆，在为理解而教（teaching for understanding，简称TFU）和为精通而教（teaching for mastery，简称TFM）两个端点之间来回摆动.基于标准的中学课程体现了为理解而教的思想.查普尔（B.Chappell）总结了基于标准的中学课程成果，基于标准的课程对中学生学习数学有积极的促进作用，包括概念与过程的理解，同时促进了学生以问题为导向的数学思维.许多基于标准的课程，反映了一些源自问题解决研究的观点.受到70年代至80年代研究的刺激，课程极大地关注问题解决.基于标准的课程为学生提供了解决问题的机会，让学生参与到数学推理中，学会用数学交流，建立数学联系等.

20世纪90年代，反改革运动在加州取得了成功，最终，加州的标准强调为精通而教，而非为理解而教.2006年9月NCTM发布了题为《幼儿园至8年级数学课程焦点》（Curriculum Focal Points for Kindergarten through Grade 8 Mathematics：A Quest for Coherence）的报告，这份报告清晰地说明了发展学生数学知识的学校数学原则与标准，报告中强调促进学生用数学解决问题，用数学进行推理、交流.