2000年起丹麦进行数学课程改革项目,针对“掌握数学”展开讨论,丹麦学者尼斯(M.Niss)指出,掌握数学就意味着拥有数学能力(mathematical competence),它指能在不同的数学背景与情景内外理解、判断和使用数学.这个项目中的能力特别强调,人们面对所给情景的数学挑战时,能够富有洞察力地准备行动,也就是说能力以行动为前提,能力不是简单地基于知识或者技能.在尼斯看来,能力具有情景性,能力发展是一个可持续的过程.该项目提出八大具体能力,它们是数学思维能力、表征能力、符号和形式化能力、交流能力、使用辅助材料与工具的能力、推理能力、建模能力以及拟题与解题(数学题处理)能力.[29]
数学思维能力内涵为:(1)能提出有数学意义的问题,并能辨识何种答案为数学答案;(2)对于给定的概念,能清楚其适用范围;(3)透过抽象化与类比扩展数学概念的范围;(4)辨识各类数学叙述(条件、定义、定理、假设臆测、数量值的叙述、案例).
数学推理能力则包括:(1)能理解别人论证的条理,并能评估该论证是否有效;(2)知道什么是数学证明,并能区分数学证明与直观的不同;(3)能从论证的条理中找到基本的想法;(4)能将直观论证转化成有效的证明.
数学建模能力是指:(1)分析数学模式的性质与属性,并评估该模式适用的范围及其效度;(2)转化或解读数学模型在现实问题中的意义;(3)在给定情境中建立数学模型.
数学拟题与解题能力主要指:(1)确认、提出及说明不同类型的数学问题(纯数学或应用;开放或封闭);(2)能解自己或别人提出的不同类型的数学问题;(3)如果合适,能以不同方法解题.
数学表征能力内涵为:(1)能解读、诠释及辨识数学对象、现象、情境的各类表征;(2)了解相同数学对象不同表征间的关系,并掌握不同表征的优势与限制;(3)可以在表征之间进行选择与转化.
符号化与形式化能力内涵为:(1)解读与诠释符号的形式数学语言,并了解它们与日常语言的关系;(2)了解数学语言的语境及语法;(3)日常语言与数学公式或(符号)语言间的转换;(4)处理和转换包含符号与公式的叙述与表达式.
数学交流能力内涵为:(1)了解别人以书面、视觉及口语所传达的数学信息;(2)能使用精确的数学语言表达自己的思想(口语的、视觉的或书面的).
辅助材料或工具使用的能力意指:(1)知道已有的数学活动工具或辅助工具的性质,并清楚其功能与限制;(2)能批判地使用这些工具或辅助工具.(https://www.xing528.com)
这八个能力与学生心理过程、数学活动有关,这些能力形成一个重心不相交却相互重叠的连续体,如图4-6所示.
这一数学能力模型强调的是数学能力首先应该是体现数学学科性的,数学能力被定义为面对特定情景中的数学挑战,人们做出有洞察力的行动准备,然后识别、直接表示和举例说明这一系列数学能力,这些数学能力各自的维度应该是相互独立的.
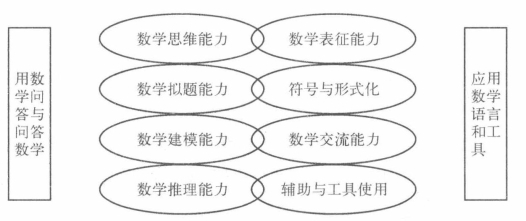
图4-6 丹麦课程改革项目提出的八大数学能力模型[30]
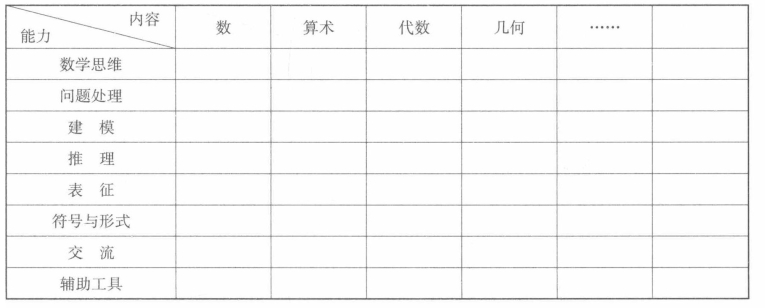
在数学课程中,这一系列数学能力与一系列数学专题,构成了一个数学内容矩阵(如表4-1),数学能力则是课程的焦点,它成为教学整体目标和教学大纲之间的纽带.
表4-1 数学内容矩阵表
数学课程改革经验已经表明,这是一个解决教学中参与问题的途径:在形成矩阵结构中作为独立维度的能力系统,使得为每项学习任务建立一个非常清晰的“合同”,一旦理解能力的本质和核心要素,学生就能够决定哪种选择是与教育重心相关的,哪种是与个人兴趣相关的.
用这种途径构造内容的主要挑战是,开发一些方法来帮助学生理解各种能力的本质与核心内涵.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




