美国中学数学课程发展研究

2.3.4.1　美国数学教育存在的问题

长期以来，美国数学课程变动幅度较小，远远跟不上科技的发展.美国传统教材在小学阶段强调计算，学生直到7、8年级才开始接触简单的代数和几何（例如常规图形的面积和体积公式），高一关注基础代数，高二学习演绎几何，高三进一步学习代数并学习三角学，高四则通常学习立体几何和高等代数.这种传统课程遭到了诸多的批评.

批评的一个核心聚焦点是：传统数学课程尤其是代数部分过分强调机械化的解题步骤，学生大多靠死记硬背的“法则”、模仿例题而不是通过理解来学习数学.例如分数的加法，学生在计算诸如时被要求严格按先通分后加减的步骤解题.优秀的课程和教师应该不遗余力地帮助学生去抓住这些步骤的基本原理，然而传统课程却没有太多关注理解.学生学习了大量的程序性知识（例如解一元方程、二元方程、多项式的加减乘除、根式的运算等），尽管这些程序性知识的掌握能够帮助学生进一步学习高等数学中的代数运算，但只注重“法则”的记忆使得学生无法灵活运用各种解题步骤.再者忽视数学的逻辑结构和系统性，人为地把数学课程分割成一些互不相通的部分，无法传递出数学的意义和精髓，学生也不能领会所学知识的意义.［53］

此外，传统数学课程的内容陈旧也受到批评.传统数学课程的大部分内容都是18世纪以前的知识，有些中学阶段仍强调的内容在20世纪已不再那么重要，例如三角学中某些知识、多项式求值的Horner法等，这些内容更适合教给致力于研究数学某方向的学生，而实际情况却是教师在没有证明的情况下花数周时间进行教学.

同时传统数学课程中存在一些逻辑问题.例如，学生被告知x2-4可因式分解为（x+2）（x-2），但x2+4和x2-2却不能被分解.然而，如果我们将“数系”扩展到复数和无理数，上述两个代数式均可分解为（x+2i）（x-2i）和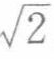（x+）（x-）.这些逻辑上的瑕疵会影响学生对数学的进一步认识和探索.

最后传统数学课程很难激发学生的学习动机.学生不知道他们为什么要学分数运算、解方程、因式分解等知识，也不清楚数学对他们的生活有何意义，体会不到数学的美.传统教学中数学被认为是思维训练的体操，数学课程更多是枯燥的练习；数值运算、代数、几何和三角学中的一些内容自1900年出版以来就几乎没有变过；加之数学教材的编辑们认为科学的编写应该是抽象的、冷酷的、机械化的等，致使学生讨厌甚至害怕数学.

2.3.4.2　美国曾经的数学课程改革

20世纪20年代末，为了满足社会化大生产的需要同时也稳定移民潮动荡的社会秩序，美国掀起第一次基础教育课程改革.此次改革以现代教育派为基础，主要是以杜威为代表的实用主义教育理论的课程为主，打破学科界限，以生活中遇到的问题为中心、按照儿童心理发展而非逻辑的顺序来组织课程，强调学生通过社会活动而非书本和教师讲授获得知识.此次课程改革过于注重实用性，忽视基础知识的学习，学生无法掌握系统的知识，致使中小学教育质量日趋低下，遭到了美国教育家、科学家的谴责.［54］

20世纪50年代，美国开始了第二次基础教育课程改革.从1955年起，政府、基金会、大学一齐出动，又着手改革中小学理科课程.1957年，苏联率先成功发射人造地球卫星，这对美国冲击极大.美国为了经济、军事扩张，急需一批科学技术尖端人才，于是加大了科学技术教育改革力度.1958年，美国国会通过《国防教育法》，其中规定增拨科学教育经费，重点改进各级学校的数学、自然科学和现代外语（称“新三艺”）的教学［55］《国防教育法》明确提出“要选拔和教育许多富有才能的儿童，由于财政原因，使缺乏能力的学生不接受高等教育是必要的，同时要求大力更新学科的教学内容”.［56］

数学教育改革首当其冲.美国的一部分数学家认为，中学里的其他科学课程，都可以反映20世纪的科学成就，如物理学的原子能，化学的各种新型塑料，生物学的遗传基因.但是，数学却只能涉及古老（特别是古希腊）内容，能够涉及17世纪的微积分已经非常“近代”了.那么数学如何反映20世纪的研究成果呢？研究的结果是，大幅度更换原有的数学内容，编写新的教材，大企业捐巨款支持改革，一时风起云涌，数学教育改革运动席卷西方世界，世称“新数运动”.［57］

“新数运动”的很大特点是把20世纪的数学内容列入中学数学课程，例如：

（1）电子计算机使用的二进制列入小学记数的要求；

（2）使用抽象集合的表示方法，以集合、属于、包含、交、并等关系作为基础；

（3）重视数系的结构，把交换律、结合律、分配律等反映数学结构的特征，以及群环域等结构，全盘引进中小学；

（4）用数集之间对应定义函数，以取代“函数是变量依赖关系”的经典定义；

（5）增加“数据处理”内容，让中小学生尽早接触随机数学.

在教学理念上也有重大变化.提倡采用发现法，认为“应当像前人发现科学规律那样进行教学”.无论怎样高深的科学成就，都能够用智力上的某种适当方式向任何年龄的学生进行解释.

此次改革的重点是中小学课程内容和教学，主要采用结构主义主张，史称“学科结构运动”.改革致力于学科知识结构、现代科学知识与旧内容的更替、学生主动学习及课程编制等问题；强调中小学课程的学术性、系统性；强调掌握各学科的基本概念、基本原理；强调发现学习.但是由于此次改革中的一些教材更多地反映学科发展及专家的要求，导致其内容过多过难，忽视了大多数学生的接受能力，加上20世纪60年代美国社会动荡不安的外因，致使改革未能达到预期目标.

2.3.4.3“新数运动”的兴起

20世纪50年代早期，美国的数学教育陷入困境，学生的数学成绩明显不如其他科目，甚至讨厌数学、害怕数学的情绪不断加重，受过教育的成人几乎连最简单的分数运算都不会.

1952年，美国的本伯曼（M.Beberman）教授开始尝试开发新的数学课程，他们编写教材、训练教师、小范围做实验.1955年，美国数学会介入，同年美国大学入学考试委员会（the college entrance examination board）为解决高中数学课程中的问题开展了大学预备数学项目（program for college preparatory mathematics）.［58］

1957年秋季，苏联发射第一颗人造卫星，西方各国受到了极大的震撼，政府和民众深刻意识到自己在数学和科学上的落后，并加大了数学课程改革的力度和资金支持.1958年，在美国数学会和美国数学教师协会（National Council of Teachers of Mathematics，简称NCTM）的支持下，由政府和基金会资助成立了“学校数学研究小组（SMSG）”，其主要成员是一些大学的数学教授，他们筹集款项，动员全国数学教育界人士和舆论，大力推进数学教育改革工作，并于1958—1959学年组织较大规模的实验（共100位教师在12个不同地方为7年级和8年级教授14个课题），培训教师并出版教材.1960年学校数学研究小组（School Mathematics Study Group，简称SMSG）将“新数”教材推向全美；美国数学教师协会组织了8场局部会议，为各地学校的新数学运动提供指导；美国数学会1961年的报告《学校数学改革》指出：“我们正处于飞速改进学校数学的关键期，一般模式已经清晰化，必备的教学材料已在手头.”［59］

由于当时人们将科技水平作为衡量社会进步的标准之一，数学对科技的作用使得“新数”很快席卷了全球.1959年，欧洲经济共同体（Organization for European Economic Cooperation，简称OEEC）成立了“科技人才组织（OSTP）”，编写出《中学数学教育现代化大纲》.1960年，日本数学教育会（Mathematics Education Society of Japan，简称JSME）召开全国数学教育研究大会，提出数学教育现代化问题.1961年，英国剑桥大学等一批学者和教师在南安普敦成立“学校数学设计组（School Mathematics Project，简称SMP）”，着手编写构思新颖、与传统数教材风格迥异的SMP课本.比较稳重的苏联，也于1965年成立了以柯尔莫戈罗夫院士为首的委员会，负责制定新的4～10年级的数学教学大纲，然后根据新大纲编写的课程终于逐步全面取代了使用达半个世纪之久的吉西略夫课本.其他如非洲、拉丁美洲、东南亚地区也都成立了区域性的机构或召开区域性会议来推进“新数”.至20世纪60年代中期，“新数”确已汇成了一股洪流，它以汹涌澎湃之势冲击旧数，对今后数学教育改革产生了不可估量的影响.［60］

2.3.4.4　“新数运动”课程的特点

尽管教学活动的结果是由诸多因素共同导致的，但“新数运动”（以下简称“新数”）却致力于数学课程（更多为教材）的改革.改革者们相信如果数学教材得到改进，数学教学将会取得成功.“新数”的实质就是课程的现代化，由于受到了布尔巴基学派及布鲁纳的结构主义课程理论的影响，一些“新数”教材将“结构”奉为指导思想之一，将数学的基本任务定位成对该学科结构的根本原理作基本理解.因此有以下特点：

强调演绎推理

针对传统数学课程中学生通过记笔记、记忆解题步骤和证明来学习数学这一主要问题，“新数”认为逻辑演绎地教数学，将每一个步骤背后的推理都揭露出来能有效地促进学生理解.逻辑法过去常被用于几何的教学，即从定义、公理、证明出发，演绎出新的定理.“新数”将其推广至数值运算、代数和三角学的教学.例如“新数”教材中负数的内容：首先让学生求方程17+x=21的解，显然答案是x=4；然后让学生解方程21+x=17，以激发学生的学习负数的动机.为了解决该问题，教材给出一系列证明，

根据定义将21分拆为17+4，则原方程改为：（17+4）+x=17，由加法结合律，得17+（4+x）=17，

根据0的定义，有17+0=17，

所以由0的唯一性，得4+x=0，

引入负数概念，4+（-4）=0，

所以，x=-4.

自此，学生在做负数运算时将有据可循，如计算（-2）+（-5）.

学生先根据负数的定义得（-2+2）+（-5+5）=0+0=0，

再由加法交换律和结合律得（-2+2）+（-5+5）=2+5+［（-2）+（-5）］，即0=7+［（-2）+（-5）］，所以（-2）+（-5）=-7.

注重严密性

“新数”中的数学课程不仅遵循演绎发展，而且追求严格的演绎发展.改革者认为对每一个结论都需要详细证明，给出其所涉及的假设、定义、定理等，哪怕是一些显然的既成事实，如两点间的距离是唯一的，一条直线将平面分成两部分，三角形有一个内部和一个外部等，否则学生会被这些未提及的假设、定理等所困扰，影响他们的理解.

力求语言精准

“新数”的改革者指出，传统数学教材中语言的不精确和宽松导致学生严重的理解障碍，例如传统教材中的应用题：“彼得有4个球，乔有5个球，他们共有多少个球？”几乎所有人都能将题意理解为“彼得和乔的球数总和是多少？”并给出答案9个.而改革者不认为这样，学生有可能给出的答案是0，因为他们两人没有一个球是共有的.为了精确语言，改革者引入集合语言、对每一个概念都精确定义，并重新定义了某些概念，例如：将题“求满足方程（equation）x+3=5的x的值”改为“求真伪未定的命题（open sentence）x+3=5的真值集合（the truth set）”；再如将传统教材中对变量的定义（变量是能被任何值替换的符号或字母）改为“变量是能被所给集合的任意元素替换的符号”.改革者在这个过程中引入了很多新术语，例如传统教材中函数被定义为变量的对应关系，而“新数”的教材在函数部分先引入“序偶集”概念，然后将函数定义为序偶的集合.库尼（T.J.Cooney）和威尔逊（M.R.Wilson）检查了1958年到1986年间出版的16种美国高中数学教材，发现它们都把函数定义为序偶的集合或两个集合元素之间的对应关系.［61］(www.xing528.com)

“自发性”的数学

“新数”将数学视为“自发性”的学科，即所有的数学知识可以不借助现实情景、自然科学等，仅由其内部发展成完整体系.例如分数的引入，可以在学生知道自然数的情况下提问学生满足3x=7的x值是多少，给学生制造认知冲突，从而引入分数的概念，同理可以通过求x+5=2的解来引入负数概念.“新数”通过对学生已有知识提出不同情景下的问题来引出新的知识，他们认为这能激发学生的学习动机并建构出整栋数学大厦.这导致“新数”课程忽视现实情景，缺乏应用性，更多的是机械练习.

加入“现代”数学

“新数”精简了部分传统数学内容，数值计算、代数、欧氏几何、三角学和基础解析几何在“新数”中都有不同程度的压缩，同时“新数”引入了诸多“现代”数学的内容.主要有：

（1）集合论：“新数”在集合基础上定义基本数学概念并且统一中学数学；

（2）进制：“新数”要求学生学会不同进制之间的转换及四则运算，以期学生能进一步理解十进制及数值运算，并对计算机的学习有帮助；

（3）同余：“新数”通过钟表上的计算引入该数论内容，要求学生理解同余概念并学会基本运算；

（4）不等式：“新数”将该内容从大学提前至9年级代数；

（5）矩阵代数：学校数学研究组（SMSG）将二次矩阵及其代数运算引入12年级；

（6）简易逻辑、布尔代数：“新数”引入命题及命题关系以期学生学会逻辑推理；

（7）群-环-域：学生不仅需要知道这些结构的概念而且要掌握其性质，一部分概念安排在小学阶段，大部分安排在高中四年级.

总之，“新数”运动在中学引进现代数学概念，使整个数学课程结构化、统一化、公理化、抽象化、现代化，同时精简了传统数学内容.

2.3.4.5　课程改革案例：SMSG

SMSG课程目标

1958年由美国耶鲁大学牵头成立学校数学研究组（SMSG），进行数学课程改革，它得到美国政府的支持和国家科学基金会的资助.SMSG集中了一批数学家、数学教师、教育学家、心理学家以及政府和实业界人士，他们于1959年就已经完成并出版中学数学试用教材，经过数次试验和修订，1962年正式出版了新的7至12年级的教科书.SMSG还编写了教师手册、教师进修读物、学生课外书籍等配套资源.［62］

SMSG课程改革的目标是，使学生有能力在未来生活中进一步学习将来所需的新数学技能.为了达到这一目标，SMSG认识到，不仅给学生提供基本的数学技能，而且使学生对数学的基础知识和结构有更深的理解；另外课程要吸引更多具有数学天赋的学生；要给教师提供帮助，使他们适应数学课程的现代化特点.

SMSG教材基本特点

SMSG教材最基本的特点表现为用现代数学的思想和语言表达传统课程的内容.在“新数”背景下，SMSG教材用现代数学的思想（如公理化思想、结构化思想、代数化思想）和语言（如集合论语言、几何变换语言）精确、严谨地表达传统课程内容.例如在7年级和8年级，SMSG教材对运算、等式、不等式、方程等基本概念赋予了现代的数学意义.在传统课程中，通过具体数字的加、减、乘、除说明运算的含义，而SMSG则用抽象的数学语言定义运算：在集合S上的二元运算*是一个指派，它指派给S中的元素的有序对（a，b）一个唯一的S中的元素c.这个定义把特殊的运算或数的运算推广到一般运算.又如在9年级，初等代数不再是用来解决繁复代数问题的分门别类的技巧和常规的机械工程，而是用统一的基本代数结构来展示数学思想，发展代数技能.

SMSG教材的另一基本特点是通过课程内容的生动设计，吸引更多有较高数学天赋的学生学习数学，注重培养数学尖子人才.一些数学家设计好SMSG教材的基本内容的同时，附设了一系列数学专题内容的介绍.他们用浅显易懂、生动有趣且富有挑战性的方法向学生介绍一般学校不再仔细探讨的数学内容.另外也注意指出数学在物理、生物、工程技术等实践领域的最新用途，启发引导学生以数学为工具探究各种先进技术与成果的奥秘.

尽管在“新数”中，许多课程改革团体推出消除欧氏几何的方案，提倡通过变换的观点或代数化的方法介绍几何，但SMSG的编者则没有抛弃欧氏几何，而是对欧氏几何的公理体系进行适当修改，采取平面几何和立体几何同时并进的设计.另外，较早地引进度量思想，如线段的长度、角的测量、平面图形的面积；采用了实数系统的性质；引进了坐标几何.SMSG教材把几何内容分散到各个年级中，从直观介绍过渡到系统严谨的理论.

SMSG教材在出版初期（20世纪60年代）在世界范围内产生巨大影响，且在试验阶段也获得一定程度的成功.但随着时间的推移，人们认识到SMSG教材过于偏重抽象理论、公理化和演绎推理方式，脱离学校数学教学的实际，造成了大量学生的基本数学技能的低下.SMSG于1973年正式宣布解散，其所编写的SMSG教材随着“新数运动”的终结成为历史，20世纪70年代后美国的数学课程在“新数学”的基础上得到了进一步发展.

2.3.4.6　“新数运动”课程的缺陷

由于“新数”的教材中涉及许多大学数学的内容，人们认为参与“新数”的学生在大学数学的学习中占有一定优势，但从数学知识点的角度出发，对比大学数学和新数学中的相应部分发现，参与“新数”并不能对大学数学的学习带来好处，甚至可能产生负面影响.例如，本伯曼教授在1960年11月的演讲中就指出，把严密性引进几何是错误的.但遗憾的是，没有关于参与“新数运动”的学生进入大学以后学习情况的大范围调查.作为SMSG的支持人，贝格勒（Begle）教授提出许多重要的看法，比如：课程设计忽略了教学法；没有更长时间的计划和更大范围的实验.1966年，SMSG组织会议为新一轮的课程改革做出详细计划，但此后数年，计划执行情况不佳，并最终导致SMSG的解散.［63］

1974年，美国有关单位成立的数学教育全国咨询委员会发表调查报告认为新教材有许多地方应该修改.社会上关于“新数运动”的批评是多数学生对于抽象的内容无法接受，基础薄弱，课程只适用一般水平以上的学生和培养少数有才能的尖子学生，忽视了面向全体学生等.美国开始倡导“回到基础”.

2.3.4.7　“新数运动”的反思与启示

反思

20世纪70年代，“新数运动”逐渐暴露出诸多不足和问题，人们开始重新审视此次改革，追寻失败的深层原因，明确改革新方向.

造成“新数运动”失败的原因是多方面的，1980年在美国伯克莱举行的第四届国际数学教育大会（ICME-4）将“新数运动”失败的主要原因总结为：（1）“新数运动”既没有系统地研究传统数学的优缺点，又没有很好地分析现代数学的背景和方法，仅将传统数学内容压缩、片面地引入现代数学概念，使得内容多而杂，跳跃性严重，时间不足.（2）现代数学内容增加太多、太深、太抽象，脱离教师和学生实际.大部分实验只面向少数成绩优异的学生，实验时间太短，内容不全面，然而实验结果的评估却宣称：学生有能力学习好新数学，并且在传统数学的技巧和知识方面表现良好，致使不少老师和学生不能适应.（3）“新数运动”是从大学到中学再到小学的自上而下的改革，改革不能切合实际需求，不宜接受和实施.［64］

究其深层原因主要有两个，一是“太过强调数学家的领导”.数学课程改革离不开数学家的指导，但不是全权领导.因为一方面，20世纪初数学发展进入新阶段，数学已从自然科学中抽离为一门独立学科，很多数学家不再关心数学的应用性，仅在数学内部做研究.［65］近代数学的发展使得数学家的研究领域非常狭窄、专业；此外当时的数学家追求纯粹的抽象化、一般化、结构化、公理化及严谨性.另一方面，数学家不是教育家，他们容易从学科视角来看教材，缺乏课改必备的教学知识和技能；大多数学家不关注数学史和数学文化，更对学习心理学不感兴趣，他们更多注重数学本身的严谨性和逻辑性.因此本次课程改革致力于数学教材的改进，而数学家所写的教材缺乏情境性及应用性，加之单调、符号化的行文风格，抽象化、结构化的内容，致使数学更加难教、难学.［66］

二是当时的社会问题.为何存在诸多问题的“新数运动”能迅速传播且被广泛接受呢？首先是课程项目的积极推广和充裕的资金支持，他们在没有大范围实验的情况下积极推广“新数”，发表演讲、文章，指责“传统”课程，为“新数”打上与时俱进、至关重要的烙印；其次是当时的中小学教师、教育家由于对数学本身的崇敬和不了解，唯数学家马首是瞻，然而数学家更多关注这场革命带来发表文章的机会；再次是绝大多数中小学校长没有审度“新数”的能力，盲目追随改革；最后是教材的编辑和出版商仅将改革视为分割市场的机会，大力宣传新教材.

启示

尽管“新数运动”最终以“回到基础”而告终，但也为今后的课程改革提供了诸多启示.

●数学教育与数学现代化

数学是一门具有严密逻辑体系，反映量与空间的抽象结构的演绎科学，但数学教育是人文教育中的一部分，中小学的数学需要置身于更广阔的文化背景下，让学生理解数学在社会文化中的角色，领会数学的价值并将数学与其他学科融会贯通.对此，中学的数学教育至少应该关注被“新数学”忽视的学生的学习动机、数学的情境性和应用性.再者，中学数学课程现代化是必要的，但同时也是一项需要循序渐进的系统工程，需要考虑其可行性，某学段的数学内容应该根据学生特点制定，教材编写和内容选取要照顾到不同层次的学生.

●课程改革不能只关注教材

1957年以后，公众及舆论对“新数”的狂热促使数学教育的专家们又把兴趣从“如何教”转向“教什么”，过分强调数学课程的内部逻辑结构，而教育是一个有机体，课程改革不能只关注教材.教师质量就是一个重要的因素，苏联提出“终身教师”口号；1982年科克罗夫特的报告中同样指出“提高数学教育质量必须解决的问题是：增加经过适当训练的数学教师，加强教师的就业前培训和在职培训”.［67］

●课程改革需协调各方力量

教育是一个社会现象，课程改革需要综合社会各界的力量，数学教育家、数学家及经验丰富的中小学数学教师都是直接参与者，而研究人员、心理学家、教育家等都能给予咨询意见，因此各力量间的协调非常重要.从“新数”看出，中小学教师才是改革的核心，数学家应作为参与者而非领导者，帮助一线教师扩张数学视野、提高数学素养、将前沿数学整合到课程中.