研究成果:箕田算题的注释

《數》的“箕田”算題原簡文是：“箕田曰：并舌步數而半之，以爲廣，道舌中丈徹中，以爲從（縱），相乘即成積步。［0936］”文中“”通“踵”。《嶽麓書院藏秦簡（貳）》的注釋提到：“此題中，箕田爲等腰梯形田地。”注釋所附圖示也是繪製的等腰梯形。^〔1〕

我們審視算題原文，並没見到任何字詞明示這一梯形田地是等腰梯形，此注釋有些不妥。郭書春在《九章算術譯注》裏對“箕田”的注釋是：“形如簸箕的田地，即一般的梯形。”^〔2〕再參看《九章算術》的箕田算題：“今有箕田，舌廣二十步，踵廣五步，正從（縱）三十步。問：爲田幾何？苔曰：一畝一百三十五步。又有箕田，舌廣一百一十七步，踵廣五十步，正從（縱）一百三十五步。問：爲田幾何？苔曰：四十六畝二百三十二步半。術曰：并踵、舌而半之，以乘正從（縱）。畝法而一。”其中的“舌廣”、“踵廣”分别是梯形的上下底，“正從（縱）”即梯形的高，“正”字更强調了“從（縱）”與“廣”的垂直特性，所給出的求解面積的方法“并踵、舌而半之，以乘正從（縱）”寫成算式“（踵+舌）÷2×正從”，等價於現今我們熟悉的一般梯形面積公式“（上底+下底）÷2×高”，魏劉徽爲《九章算術》作注時進而指出：“中分箕田則爲兩邪田，故其術相似。又可並踵、舌，半正從（縱）以乘之。”更明確區分“箕田”與“邪田”。所謂“邪田”的形狀，就是指一條側邊與上下底邊垂直的梯形，《九章算術》裏也有關於“邪田”的算題。^〔3〕這就是説，《九章算術》裏的“箕田”指的是一般梯形，而不是某種特殊梯形，因此，解釋“箕田”爲等腰梯形是不恰當的。

《數》的“箕田”算題原簡文是：“箕田曰：并舌步數而半之，以爲廣，道舌中丈徹中，以爲從（縱），相乘即成積步。［0936］”文中“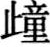”通“踵”。《嶽麓書院藏秦簡（貳）》的注釋提到：“此題中，箕田爲等腰梯形田地。”注釋所附圖示也是繪製的等腰梯形。^〔1〕

我們審視算題原文，並没見到任何字詞明示這一梯形田地是等腰梯形，此注釋有些不妥。郭書春在《九章算術譯注》裏對“箕田”的注釋是：“形如簸箕的田地，即一般的梯形。”^〔2〕再參看《九章算術》的箕田算題：“今有箕田，舌廣二十步，踵廣五步，正從（縱）三十步。問：爲田幾何？苔曰：一畝一百三十五步。又有箕田，舌廣一百一十七步，踵廣五十步，正從（縱）一百三十五步。問：爲田幾何？苔曰：四十六畝二百三十二步半。術曰：并踵、舌而半之，以乘正從（縱）。畝法而一。”其中的“舌廣”、“踵廣”分别是梯形的上下底，“正從（縱）”即梯形的高，“正”字更强調了“從（縱）”與“廣”的垂直特性，所給出的求解面積的方法“并踵、舌而半之，以乘正從（縱）”寫成算式“（踵+舌）÷2×正從”，等價於現今我們熟悉的一般梯形面積公式“（上底+下底）÷2×高”，魏劉徽爲《九章算術》作注時進而指出：“中分箕田則爲兩邪田，故其術相似。又可並踵、舌，半正從（縱）以乘之。”更明確區分“箕田”與“邪田”。所謂“邪田”的形狀，就是指一條側邊與上下底邊垂直的梯形，《九章算術》裏也有關於“邪田”的算題。^〔3〕這就是説，《九章算術》裏的“箕田”指的是一般梯形，而不是某種特殊梯形，因此，解釋“箕田”爲等腰梯形是不恰當的。(www.xing528.com)

我們爲書作注時之所以解釋“箕田”爲等腰梯形，有兩個原因：一是認爲簡文所記的算法必定正確；二是對“道舌中丈徹（踵）中，以爲從（縱）”一句的理解有偏差。簡文給出的“箕田”面積算法是：“（舌+）÷2×從”，要使得此算法正確，那麽“道舌中丈徹（踵）中，以爲從（縱）”這一步驟求得的量必須是梯形的高。若假定此處“箕田”爲等腰梯形，則從上底中點到下底中點的連綫正是梯形的高，如此則簡文所述算法正確。但問題在於“中”不一定指中點，“舌中”、“（踵）中”可能指“舌”、“（踵）”，即上下底邊的任意一點，且“箕田”應是一般梯形，那麽“道舌中丈徹（踵）中”求得的量很難恰是梯形的高，《數》記載的“箕田”面積算法就不準確。除非能證明，“道舌中丈徹（踵）中，以爲從（縱）”表示了所求“從（縱）”垂直於“舌”、“（踵）”兩底邊的含義。“道”在書中注釋爲“從”、“由”，或可解釋爲“方法”，文意也是通順的。“丈徹”，書中注釋“丈，丈量。徹，通，穿”。文意即從“舌中”的一點開始測量，穿過田地直到“（踵）中”的一點，但“丈徹”是否有垂直底邊的含義，尚未在已知的古算書裏發現佐證。林力娜（Karine Chemla）提出，如果在中國古算書裏（或者至少在秦漢時期的算書裏），“廣”指嚴格意義上的東西向長度，“縱”指嚴格意義上的南北向長度，則“廣”、“縱”間存在垂直關係，假若有這一前提條件，那麽簡文“并舌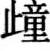步數而半之，以爲廣，道舌中丈徹中，以爲從（縱）”就已包含了垂直關係，算法成立。^〔4〕可是此説仍然缺乏證據，雖然“東西爲廣，南北爲縱”多有書證，但是“廣”、“縱”的定義並不如“經”、“緯”般確切，不能斷定古算書裏的術語“廣”與“縱”之間暗含垂直關係。

我們爲書作注時之所以解釋“箕田”爲等腰梯形，有兩個原因：一是認爲簡文所記的算法必定正確；二是對“道舌中丈徹（踵）中，以爲從（縱）”一句的理解有偏差。簡文給出的“箕田”面積算法是：“（舌+）÷2×從”，要使得此算法正確，那麽“道舌中丈徹（踵）中，以爲從（縱）”這一步驟求得的量必須是梯形的高。若假定此處“箕田”爲等腰梯形，則從上底中點到下底中點的連綫正是梯形的高，如此則簡文所述算法正確。但問題在於“中”不一定指中點，“舌中”、“（踵）中”可能指“舌”、“（踵）”，即上下底邊的任意一點，且“箕田”應是一般梯形，那麽“道舌中丈徹（踵）中”求得的量很難恰是梯形的高，《數》記載的“箕田”面積算法就不準確。除非能證明，“道舌中丈徹（踵）中，以爲從（縱）”表示了所求“從（縱）”垂直於“舌”、“（踵）”兩底邊的含義。“道”在書中注釋爲“從”、“由”，或可解釋爲“方法”，文意也是通順的。“丈徹”，書中注釋“丈，丈量。徹，通，穿”。文意即從“舌中”的一點開始測量，穿過田地直到“（踵）中”的一點，但“丈徹”是否有垂直底邊的含義，尚未在已知的古算書裏發現佐證。林力娜（Karine Chemla）提出，如果在中國古算書裏（或者至少在秦漢時期的算書裏），“廣”指嚴格意義上的東西向長度，“縱”指嚴格意義上的南北向長度，則“廣”、“縱”間存在垂直關係，假若有這一前提條件，那麽簡文“并舌步數而半之，以爲廣，道舌中丈徹中，以爲從（縱）”就已包含了垂直關係，算法成立。^〔4〕可是此説仍然缺乏證據，雖然“東西爲廣，南北爲縱”多有書證，但是“廣”、“縱”的定義並不如“經”、“緯”般確切，不能斷定古算書裏的術語“廣”與“縱”之間暗含垂直關係。